
MS_bak_220400_220700
.pdf
Окончание таблицы 2.5.
№вар\№оп |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
|
||||||||||||||||||||
14 |
x |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
10,0 |
11,0 |
12,0 |
13,0 |
14,0 |
15,0 |
16,0 |
17,0 |
18,0 |
19,0 |
20,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
0,95 |
1,56 |
1,91 |
2,16 |
2,35 |
2,51 |
2,64 |
2,76 |
2,86 |
2,95 |
3,04 |
3,11 |
3,18 |
3,25 |
3,31 |
3,36 |
3,42 |
3,47 |
3,51 |
3,56 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
x |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2,0 |
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
129,7 |
128,1 |
126,7 |
125,3 |
124,1 |
122,9 |
121,7 |
120,4 |
119,2 |
117,9 |
116,5 |
114,9 |
113,3 |
111,3 |
108,9 |
105,9 |
102,0 |
96,62 |
88,25 |
73,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
x |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
1,21 |
4,79 |
10,62 |
18,49 |
28,06 |
38,96 |
50,75 |
62,96 |
75,1 |
86,69 |
97,26 |
106,4 |
113,7 |
118,9 |
121,9 |
122,4 |
120,5 |
116,2 |
109,7 |
101, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
x |
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
2,2 |
2,4 |
2,6 |
2,8 |
3,0 |
3,2 |
3,4 |
3,6 |
3,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
2,28 |
2,26 |
2,19 |
2,09 |
1,97 |
1,85 |
1,74 |
1,65 |
1,56 |
1,58 |
1,6 |
1,65 |
1,71 |
1,78 |
1,84 |
1,87 |
1,88 |
1,86 |
1,8 |
1,74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
x |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
7,0 |
7,05 |
7,1 |
7,2 |
7,2 |
7,28 |
7,36 |
7,16 |
7,59 |
7,76 |
7,99 |
8,35 |
8,95 |
10,12 |
13,61 |
37,21 |
32,2 |
10,65 |
7,28 |
6,21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
x |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
7,0 |
7,5 |
8,0 |
8,5 |
9,0 |
9,5 |
10,0 |
10,5 |
11,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
29,5 |
29,6 |
29,7 |
29,8 |
29,9 |
31,0 |
31,1 |
31,8 |
32,6 |
33,8 |
34,7 |
35,8 |
36,8 |
37,7 |
38,3 |
38,7 |
38,9 |
39,2 |
39,3 |
39,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
x |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
10,0 |
11,0 |
12,0 |
13,0 |
14,0 |
15,0 |
16,0 |
17,0 |
18,0 |
19,0 |
20,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
11,0 |
12,3 |
13,2 |
14,1 |
14,0 |
11,5 |
11,2 |
12,0 |
12,8 |
14,0 |
14,1 |
11,6 |
11,0 |
12,1 |
13,6 |
14,3 |
12,1 |
11,1 |
12,2 |
13,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
x |
0,0 |
0,3 |
0,6 |
0,9 |
1,2 |
1,5 |
1,8 |
2,1 |
2,4 |
2,7 |
3,0 |
3,3 |
3,6 |
3,9 |
4,2 |
4,5 |
4,8 |
5,1 |
5,4 |
5,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
24,89 |
23,2 |
21,69 |
20,36 |
19,18 |
18,14 |
17,21 |
16,4 |
15,66 |
14,88 |
14,1 |
11,6 |
11,0 |
12,1 |
13,6 |
14,3 |
12,1 |
11,1 |
12,2 |
13,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
x |
0,10 |
0,11 |
0,12 |
0,13 |
0,14 |
0,15 |
0,16 |
0,17 |
0,18 |
0,19 |
0,20 |
0,21 |
0,22 |
0,23 |
0,24 |
0,25 |
0,26 |
0,27 |
0,28 |
0,29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
1040 |
856 |
734,4 |
613,7 |
550,2 |
481,4 |
430,6 |
386,6 |
387 |
348,7 |
290 |
266,8 |
246,6 |
229 |
213 |
199,9 |
188 |
177,2 |
167,5 |
158, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
x |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
0,10 |
0,11 |
0,12 |
0,13 |
0,14 |
0,15 |
0,16 |
0,17 |
0,18 |
0,19 |
0,20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
1003 |
504 |
337,3 |
254 |
204 |
170,6 |
146,8 |
129 |
115,1 |
104 |
94,9 |
87,4 |
81 |
75,4 |
70,7 |
66,5 |
62,8 |
59,6 |
56,6 |
54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
x |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
71 |
71,6 |
71,9 |
72,6 |
73,4 |
74,2 |
75 |
75,6 |
76,2 |
76,6 |
77,1 |
77,5 |
77,8 |
78,2 |
78,4 |
78,6 |
78,8 |
78,9 |
79 |
79,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
x |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
10,0 |
11,0 |
12,0 |
13,0 |
14,0 |
15,0 |
16,0 |
17,0 |
18,0 |
19,0 |
20,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
14 |
12,8 |
11,2 |
11 |
10,8 |
10,8 |
10,8 |
10,8 |
10,8 |
10,8 |
10,8 |
10,8 |
10,8 |
10,8 |
10,8 |
10,8 |
11 |
11,2 |
12,8 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
x |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
10,0 |
11,0 |
12,0 |
13,0 |
14,0 |
15,0 |
16,0 |
17,0 |
18,0 |
19,0 |
20,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
17,1 |
15 |
13,1 |
12,6 |
12,5 |
12,8 |
13 |
13,6 |
13,9 |
14,2 |
14,6 |
14,8 |
15,2 |
15,4 |
15,6 |
15,8 |
16 |
16,2 |
16,4 |
16,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51

|
|
|
|
|
|
|
|
Таблица 2.6. |
|||||
|
|
Типы уравнений регрессии |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Тип кривой |
Уравнение |
Замена |
Замена |
Уравнение |
|||||||||
|
регрессии |
x |
y |
в новых |
|||||||||
|
|
|
|
|
|
|
|
координатах |
|||||
1 |
|
2 |
|
|
3 |
4 |
5 |
|
|
|
|||
|
yˆ a x b |
- |
- |
- |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
yˆ b x a |
u lg x |
zˆ lg yˆ |
zˆ a u lg b |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yˆ |
x |
|
lg b |
|
u x |
zˆ ln yˆ |
zˆ a u lnb |
|||||
|
|
|
|
|
|
|
|
|
|||||
|
lg a |
lg a |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
yˆ loga bx |
u lg x |
zˆ yˆ |
zˆ |
u |
|
lg b |
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
lg a |
|
lg a |
|
||
|
|
|
|
|
|||||||||
|
yˆ a ln bx |
u ln x |
zˆ yˆ |
zˆ a u |
|||||||||
|
|
|
|
|
|
|
|
a ln b |
|||||
|
|
|
|
|
|||||||||
|
yˆ a lg bx |
u lg x |
zˆ yˆ |
zˆ a u |
|||||||||
|
|
|
|
|
|
|
|
a lgb |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52 |
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
Продолжение табл. 2.6. |
||
1 |
2 |
3 |
|
4 |
5 |
yˆ |
1 |
u x |
zˆ |
1 |
zˆ a u b |
|
|
||||
|
a x b |
|
|
yˆ |
|
yˆ |
x |
u x |
zˆ x |
zˆ a u b |
|
|
|
||||
|
a x b |
|
|
yˆ |
|
yˆ a x2 b x с |
- |
- |
|
- |
|
yˆ2 a x2 b x с |
u x |
zˆ yˆ 2 |
|
||
yˆ |
1 |
u x |
zˆ |
1 |
|
a x2 b x с |
|
|
|||
|
|
|
|
yˆ |
|
yˆ |
x |
u x |
zˆ x |
|
|
a x2 b x с |
|
|
|||
|
|
|
|
yˆ |
|
|
|
|
|
|
53 |

|
|
|
|
|
Окончание табл. 2.6. |
|
1 |
|
2 |
3 |
4 |
5 |
|
yˆ a2 |
b с |
u 1 |
zˆ yˆ |
|
||
x |
|
|
x |
x |
|
|
ˆ |
2 |
x b lg x |
u lg x |
zˆ yˆ |
|
|
y a lg |
|
|
|
|||
с |
|
|
|
|
|
|
yˆ a ln2 x b ln x |
u ln x |
zˆ yˆ |
|
|||
с |
|
|
|
|
|
|
ˆ |
|
2 |
x b sin x |
u sin x |
zˆ yˆ |
|
y a sin |
|
|
||||
с |
|
|
|
|
|
|
yˆ a cos2 |
x b cos x |
u cos x |
zˆ yˆ |
|
||
с |
|
|
|
|
|
|
yˆ a tg 2 x b tgx |
u tgx |
zˆ yˆ |
|
|||
с |
|
|
|
|
|
|
54 |
|
|
|
|
|
|
Глава 3. МОДЕЛИРОВАНИЕ, РАСЧЕТ И ИССЛЕДОВАНИЕ ЦИФРОВЫХ СИСТЕМ УПРАВЛЕНИЯ
Интенсивное развитие средств вычислительной техники (СВТ) привело к широкому распространению цифровых систем управления (ЦСУ) [6,9]. Этому способствовало создание микропроцессоров и микропроцессорной техники. Методы проектирования ЦСУ существенно отличаются от классических методов, применяемых для аналоговых систем. Основой математического аппарата построения цифровых систем являются разностные схемы, описывающие функционирование дискретных систем, которые значительно проще с точки зрения их анализа и программной реализации, нежели дифференциальные уравнения, применяемые для описания непрерывных систем.
При синтезе систем автоматического управления, реализуемых на средствах вычислительной техники, появляется возможность разработки достаточно сложных алгоритмов оптимального цифрового управления, что позволяет наиболее полно учесть особенности объектов управления. Этого можно достичь за счет исключения трудоемких аналитических преобразований, т. к. при синтезе цифровых систем основные этапы расчета выполняются на ЭВМ с использованием численных методов.
3.1.Построение динамических моделей объектов
управления |
с |
помощью |
разностных |
уравнений |
и дискретных передаточных функций |
|
|||
Из теории автоматического управления известно, что модели динамических объектов с запаздыванием (рис. 3.1) в непрерывном виде могут быть представлены дифференциальными уравнениями или соответствующими передаточными функциями:
T n |
d n y t |
|
T n 1 |
d n 1 y t |
|
... T 1 |
dy t |
|
y t ku t (3.1) |
|
|
|
|||||||
n |
dt n |
n 1 |
dt n 1 |
1 |
dt |
|
|||
|
|
|
|
||||||
или
55

W s |
y s |
|
|
|
ke s |
|
|
|
|
|||
u s |
1 |
T s 1 T s ... 1 T |
s |
|||||||||
|
|
|
|
|||||||||
|
|
|
|
|
1 |
2 |
n |
|
|
(3.2) |
||
|
|
|
ke s |
|
|
|
|
|
|
|||
|
|
|
|
|
, |
|
|
|
|
|||
1 T 1s T 2s2 ... T n sn |
|
|
|
|
||||||||
1 |
|
2 |
|
|
n |
|
|
|
|
|||
где y - выходной сигнал объекта; u - входной сигнал; k - коэффициент усиления; - время чистого запаздывания; s - оператор
преобразования Лапласа; T1, T2 ,..., Tn |
- постоянные времени объ- |
||||||||||||||||
екта, |
по |
|
которым |
могут |
вычисляться |
|
|
коэффициенты |
|||||||||
T1 |
, T 2 |
,..., T n |
дифференциального уравнения (3.1): |
|
|
|
|||||||||||
1 |
2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при n 1 |
T1 |
T , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
при n 2 |
T1 |
T T |
, T 2 |
TT , |
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
1 |
2 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
при n 3 |
T1 |
T |
T |
T |
, T 2 |
TT TT T T |
, T 3 |
TT T . |
|||||||||
|
|
|
1 |
1 |
2 |
3 |
2 |
1 |
2 |
1 |
3 |
2 |
3 |
3 |
1 |
2 |
3 |
Рис. 3.1. Динамическое звено с одним входом и выходом
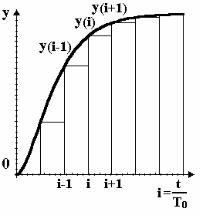
Непрерывная модель (3.1), описывающая поведение объекта с сосредоточенными параметрами, представляет собой непрерывную функцию y t и может быть интерпретирована в виде
графика (рис. 3.2) [6].
Если весь диапазон времени разбить на равные интервалы - период (такт) квантования T0 и обозначить текущий номер такта
i , то получим ряд дискретных значений на непрерывной кривой
(рис. 3.2).
При малых тактах квантования T0 из дифференциальных
уравнений (3.1) можно получать разностные путем дискретизации. В частности, дифференциалы могут приближенно заменяться правыми, левыми или центральными разностями.
56
При использовании правых разностей:
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||||
|
|
|
|
|
dy |
|
|
y i |
|
|
|
y |
1 |
y i |
|
, |
|
|
|
||||||
|
|
|
|
|
dt |
|
T0 |
|
|
|
|
T0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
d 2 y t |
|
2 y i |
|
y i 1 2 y i y i 1 |
, |
|
(3.3) |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
dt2 |
|
|
|
T |
2 |
|
|
|
|
|
|
T 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
d 3 y t |
|
3 y i |
|
y i 1 3y i 3y i 1 y i 2 |
. |
|
|||||||||||||||||||
dt3 |
|
T 3 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
3 |
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
Рис. 3.2. График функции y t
Таким образом можно получить уравнение n -го порядка в разностном виде при известных параметрах дифференциального уравнения (3.1):
T n n yi T n 1 |
n 1 yi ... T1 |
yi y |
ku |
. (3.4) |
|||
n T n |
n 1 |
T n 1 |
1 |
T |
i |
i d |
|
0 |
|
0 |
|
0 |
|
|
|
При этом непрерывной передаточной функции (3.2) будет соответствовать дискретная передаточная функция:
W z |
y z |
|
|
B z z d 1 |
, |
(3.5) |
|
u z |
A z |
||||||
|
|
|
|
||||
|
|
|
|
|
|
57 |
|

где B z , A z - полиномы числителя и знаменателя дискретной
передаточной функции; z - оператор сдвига; d T0 - целое
число тактов запаздывания, соответствующее времени чистого запаздывания .
Если d при вычислении не является целым числом, то оно округляется до ближайшего целого.
Например, апериодическое звено второго порядка ( n 2 ) с чистым запаздыванием представляется в виде дифференциаль-
ного уравнения второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
T 2 |
d 2 y t |
|
T1 |
|
dy t |
y t ku t , |
|
|
|
|
(3.6) |
||||||||||||||||||
|
|
dt2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 |
|
1 |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
или соответствующей передаточной функцией |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
W s |
|
|
|
|
|
ke s |
|
|
|
. |
|
|
|
|
|
|
|
|
(3.7) |
||||||
|
|
|
|
|
|
1 T1s T 2s2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Из дифференциального уравнения (3.6) получим конечно- |
|||||||||||||||||||||||||||||||
разностное: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
T 2 |
yi 1 2 yi |
yi 1 |
|
T1 |
|
yi 1 |
yi |
y |
ku |
. |
|
(3.8) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2 |
|
|
|
T 2 |
|
|
|
|
|
1 |
|
|
T |
|
|
i |
|
i d |
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Преобразуя это уравнение, выразим из него yi 1 : |
|
|
|
||||||||||||||||||||||||||||
|
|
T1T 2T 2 |
T 2 |
|
|
|
|
|
T 2 |
|
|
|
|
|
|
kT2 |
|
|
|
|
|
||||||||||
y |
1 0 |
|
2 |
|
|
0 |
y |
|
|
|
|
|
2 |
|
y |
|
0 |
|
|
u |
|
. (3.9) |
|||||||||
T 2 |
T1T |
|
|
|
T 2 T1T |
T 2 |
T1T |
|
|||||||||||||||||||||||
i 1 |
|
|
i |
|
|
|
|
i 1 |
|
|
|
i d |
|
||||||||||||||||||
|
|
2 |
1 |
0 |
|
|
|
|
|
|
2 |
|
1 |
0 |
|
|
|
2 |
1 |
0 |
|
|
|
|
|||||||
Введем обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
a |
T1T 2T 2 |
T 2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 0 |
|
|
|
2 |
0 |
, |
|
|
|
|
|
(3.10) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
T 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
T1T |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
a2 |
|
|
2 |
|
, |
|
|
|
|
|
|
|
|
(3.11) |
|||||||||
|
|
|
|
|
|
|
|
T 2 |
|
T1T |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
58 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
kT2 |
|
|
|
0 |
|
. |
(3.12) |
|
|
|
|||
|
T22 T11T0 |
|
||
Отсюда |
|
|
|
|
yi 1 a1 yi a2 yi 1 |
bui d . |
(3.13) |
||
Уменьшая текущий индекс такта квантования на единицу в левой и правой частях уравнения (3.13), получим конечноразностное уравнение второго порядка, удобное для практического использования:
yi a1 yi 1 a2 yi 2 bui d 1. |
(3.14) |
Для расчета переходного процесса звена по разностному уравнению (3.14) целесообразно принимать начальные условия нулевыми (выполнять расчет в приращениях). При этом началь-
ные условия определяются порядком уравнения: |
|
|
|||||
|
|
|
y1 ... y2 d 0 , u1 0 . |
|
(3.15) |
||
|
Если на вход модели подается единичное ступенчатое воз- |
||||||
действие, |
то, начиная с такта |
квантования |
i 2 , |
ui 1 |
|||
i |
|
. |
|
|
|||
2, N |
N определяется временем переходного процесса tп : |
||||||
|
|
|
N |
tп |
. |
|
(3.16) |
|
|
|
|
|
|||
|
|
|
|
T |
|
|
|
|
|
|
|
0 |
|
|
|
Так как tп |
заранее не известно, то число N выбирается экспери- |
||||||
ментально подбором при расчете переходного процесса.
Расчет переходного процесса по рекуррентному уравнению (3.14) начинается с такта i 3 d (во избежание появления отрицательных индексов в массиве y ):
y3 d y4 d
y5 d
.
a1 y2 d
a1 y3 d
a1 y4 d
.
a2 y1 d bu2 b , |
(3.17) |
a2 y2 d bu3 b a1 1 , |
|
a2 y3 d bu4 a1b a1 1 b a2 1 ,
.
yN d a1 yN 1 d a2 yN 2 d buN 1 ,
59
yN d 1 a1 yN d a2 yN 1 d buN .
По аналогии с формулами (3.10) - (3.12) получены зависимости прямой и обратной взаимосвязи между параметрами непрерывных и дискретных динамических моделей 1-го - 4-го порядков с заданным тактом квантования T0 (табл. 3.1, 3.2) [6].
Использование табл. 3.1, 3.2 упрощает пересчет моделей в ходе требуемых исследований.
Для систем, представленных линейными разностными уравнениями с постоянными коэффициентами, также используется операционное исчисление, в котором входные и выходные величины описываются оператором сдвига z аналогично оператору Лапласа s :
y |
i |
yz 0 y, |
u |
|
uz 0 u, |
|
||||
|
|
yz 1 |
|
i |
|
|||||
y |
|
|
, |
|
|
|
|
|
||
i |
1 |
u |
|
|
uz 1 , |
(3.18) |
||||
|
|
|
i |
1 |
||||||
|
|
. . . |
|
|
|
|
|
|||
|
|
|
u |
|
|
|
uz d 1. |
|
||
y |
|
|
yz n , |
i |
d 1 |
|
||||
|
|
|
|
|
||||||
i |
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Использование оператора сдвига |
|
z позволяет получить из |
||||||||
конечно-разностного уравнения передаточную функцию. Например, для уравнения второго порядка (3.14) получим:
yz0 a yz 1 a yz 2 buz d 1. |
(3.19) |
|||||
1 |
|
2 |
|
|
|
|
Отсюда дискретная передаточная функция: |
|
|||||
W z |
y z |
|
bz d 1 |
|
. |
(3.20) |
|
1 a z 1 a z 2 |
|||||
|
u z |
|
|
|||
|
|
|
1 |
2 |
|
|
Аналогично можно получить разностные уравнения и дискретные передаточные функции объектов, описываемых интегродифференциальными уравнениями любого порядка (табл. 3.3).
60
