MS_bak_220400_220700

Постановка задачи

Выбор цели, критериев, параметров объекта моделирования

Разработка математического описания

Экспериментально-статистическое описание Детерминированное описание

Разработка алгоритма решения и программирование

Выбор метода решения, разработка алгоритма, выбор языка программирования, программирование, отладка программы

Установление адекватности модели реальному объекту (по экспериментальным данным)

Использование модели (в зависимости от цели моделирования)

Рис. 1.1. Схема этапов математического моделирования

По целевому назначению модели делятся на следующие классы [3-5]:

-модели для оптимального проектирования процессов и систем (САПР);

-модели для исследования и оптимизации действующих технологических установок и систем (для работающих производств);

-модели для целей управления.

Соответственно различаются и постановки задач для каждого класса (различия относятся к выбору параметров состояния, формированию критериев оптимальности, степени детализации модели).

Например, при проектировании новой установки ставится задача расчета ее конструктивных параметров на модели, а при исследовании действующей установки - конструктивные параметры будут фиксированы. Другой пример – к моделям, разрабатываемым для целей управления, предъявляются требования по

11

быстродействию (время воспроизведения режима работы аппарата не должно превышать время переходного процесса).

Математические модели классифицируются также по ряду признаков [2]: степени абстрагирования; форме представления; характеру отображаемых свойств; способу получения модели; способу реализации модели; математическому аппарату.

Классификация в зависимости от степени абстрагирования при описании свойств системы.

Метауровень соответствует наиболее крупному масштабу проектирования, в котором рассматривается объект в целом и осуществляется научный поиск, прогнозирование и разработка концепции математической модели. Для метауровневых моделей характерно использование методов теории графов, математической логики, теории конечных автоматов, теории массового обслуживания, теории автоматического управления.

Макроуровень соответствует большему масштабу детализации системы. Объект рассматривается как совокупность взаимодействующих между собой отдельных функциональных элементов. Для макроуровневых моделей характерно математическое описание составных частей объекта уравнениями с сосредоточенными параметрами.

Микроуровень соответствует наиболее детальному масштабу изучения системы. Рассматривается состояние и поведение отдельных функциональных элементов системы с учетом внутреннего состояния каждого отдельного элемента. Для микроуровневых моделей характерно детальное математическое описание составных частей объекта с учетом внутреннего состояния отдельных элементов при помощи уравнений с сосредоточенными и распределенными параметрами.

Классификация в зависимости от формы представления математических моделей.

Инвариантная модель. Математическая модель представлена в виде функциональных соотношений (алгебраических, интегральных, дифференциальных, конечно-разностных и т. п.) и логических условий вне связи с методами преобразования этих функциональных соотношений (решения уравнений, упрощения логических условий и т. п.).

Аналитическая модель. Математическая модель в виде яв-

12

ных общих зависимостей между входными, выходными переменными и параметрами объекта. Эти зависимости могут быть получены двумя путями:

-непосредственные модели получают путем аналитического решения уравнений инвариантной модели.

-идентификационные модели получают путем решения обратной задачи (задачи идентификации) на основе экспериментальных данных, описывающих поведение объекта, при помощи одного из методов идентификации: регрессионного анализа, спектрального оценивания и т. д.

Алгоритмическая модель. Математическая модель в виде частных зависимостей между входными, выходными переменными и параметрами объекта:

-для численных моделей эти зависимости получают путем численного решения соответствующих уравнений инвариантной модели;

-в имитационных моделях для получения частной зависимости между входными, выходными переменными и параметрами объекта производится эксперимент на модели при заданных исходных данных. В имитационной модели поведение компонент сложной системы описывается набором алгоритмов, которые затем реализуют ситуации, возникающие в реальной системе. Имитационное моделирование предполагает изучение некоторого моделирующего алгоритма, имитирующего процессы объектаоригинала [10];

-интеллектуальные модели - это отдельный вид алгоритмических моделей, бывший ранее подвидом имитационных моделей и выделившийся в отдельную группу благодаря развитию методов искусственного интеллекта и разработке так называемых «мягких вычислений», основанных на генетических алгоритмах, нейронных сетях, нечетких множествах и других методах искусственного интеллекта [12].

Графическая модель. Математическая модель в виде графиков, функциональных, кинематических и алгоритмических схем, диаграмм, циклограмм, графов, таблиц и т. п. Для создания графической модели необходимо существование правила однозначного соответствия компонент инвариантной математической модели в графическом виде.

13

Классификация по характеру отображаемых свойств объекта.

Структурная модель отражает общую структуру объекта на метауровне и используется для решения задач структурного синтеза и выбора общего технического решения.

Функциональная модель описывает процесс функционального преобразования сигналов в рамках функционирования как объекта в целом, так и его составных частей. Используется на макроуровне для решения задач выбора элементов автоматики, согласования соседствующих элементов по характеру сигналов (роду энергии и виду сигналов), а также выбору параметров составных частей объекта управления.

Технологическая модель представляет собой систему конкретных технических решений, связанных с процессом изготовления объекта.

Классификация по способу получения.

Теоретическая модель строится на основе изучения закономерностей функционирования объекта и описания процессов его функционирования. При построении теоретической модели учитываются внутренние свойства объекта и процессы взаимодействия между отдельными компонентами системы.

Эмпирическая модель строится на основе изучения внешних проявлений свойств объекта и поведения объекта во внешней среде в качестве «черного ящика». При построении эмпирической модели математически описываются экспериментально установленные связи между отдельными параметрами системы, без учета характера законов, вызвавших появление этих связей.

Комбинированные модели строятся на основе комбинации вышеописанных теоретических и эмпирических методов построения, как правило, в случае, когда экспериментальные зависимости, от которых отталкиваются при построении эмпирической модели, получены не при физическом эксперименте на реальном объекте, а при вычислительном эксперименте на математической модели этого объекта.

Классификация по характеру математического аппарата.

Линейные / Нелинейные - в зависимости от линейности / нелинейности математических зависимостей, входящих в модель.

14

Непрерывные / Дискретные - в зависимости от характера изменения переменных, фигурирующих в модели.

Детерминированные / Статистические - в зависимости от того, отражает ли математический аппарат случайный характер параметров объекта и свойств внешней среды.

Статические / Динамические - в зависимости от того, отражает ли математический аппарат изменение во времени параметров объекта и свойств внешней среды.

Классификация по способу реализации.

Аналоговые модели реализуются на аналоговых вычислительных машинах (АВМ), носителем информации в которых являются непрерывные сигналы. Аналоговое моделирование основывается на свойствах изоморфизма различных физических явлений. Изоморфизм заключается в том, что различные по своей физической природе процессы описываются одинаковыми математическими конструкциями.

Цифровые модели реализуются на цифровых вычислительных машинах (ЦВМ), носителем информации в которых являются дискретные сигналы. Сущность цифрового моделирования состоит в реализации математических моделей средствами прикладного программного обеспечения ЦВМ.

Гибридные модели реализуются на аналого-цифровых вычислительных машинах и комплексах (АЦВМ, АЦВК), сочетающих достоинства аналогового и цифрового моделирования: скорость и точность АВМ, гибкость, наглядность и удобство ЦВМ.

Нейронечеткие модели реализуются при помощи интеллектуальных вычислительных устройств нового поколения, реализующих так называемые «мягкие вычисления»: нейрокомпьютеров и нечетких вычислительных систем, алгоритм работы которых базируется на методах, принципиально отличных от двоичной логики. Нейрокомпьютеры - вычислительные системы, представляющие сеть специализированных элементов (нейронов), имитирующих биологическую мозговую деятельность. Нечеткие вычислительные системы имитируют способность человеческого мозга работать с нечетко определенными понятиями, не имеющими однозначной численной интерпретации («большое давление», «малая скорость» и т. п.) [12]. Следует различать нейронечеткое моделирование как способ реализации моделей при по-

15

мощи вычислительных устройств, построенных на нейронных и нечетких процессорах, и нейронечеткую форму представления математических моделей, которая реализована при помощи прикладного ПО ЦВМ, имитирующего работу систем нечеткого вывода и нейронных сетей в классе алгоритмических интеллектуальных моделей.

1.2. Подходы к построению математических моделей

Существует два основных подхода к составлению математических моделей: экспериментально-статистический и детерминированный [1,2].

При детерминированном подходе математическое описание составляется на основе фундаментальных теоретических законов (например, законов сохранения массы и энергии, термодинамики, химической кинетики и т. д.). При этом учитываются такие явления как диффузия, тепло- и массапередача, гидродинамика и т. д.

Например, перенос энергии описывается законом Ньютона:

где i - сила тока; - коэффициент электрического сопротивле-

ния; dudx - градиент напряжения по линейной координате x .

Если ввести пересчетные коэффициенты, то перенос энергии можно моделировать переносом электричества. Это называется принцип аналогий.

16

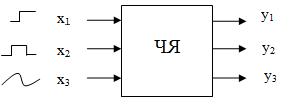
Экспериментально-статистический подход основан на обработке экспериментальных данных. При этом структура интересующего нас объекта скрыта, т. е. как бы заключена в “черный ящик” (рис. 1.2). Проводя эксперимент (задавая входные воздействия и получая выходные – отклик) набираются значения входных и выходных параметров. Затем проводится обработка статистических данных.

Рис. 1.2. Структурная схема модели при экспериментальностатистическом подходе: ЧЯ – “черный ящик”; x1, x2, x3 – входные параметры; y1, y2, y3 – выходные параметры

1.3. Структура математического описания при детерминированном подходе

В состав математического описания при детерминированном подходе входят следующие группы уравнений:

1. Уравнения, основанные на законах сохранения массы и энергии:

а) обобщенные уравнения материального и теплового балансов для нестационарных процессов;

Такие уравнения описывают процессы в переходном режи-

ме.

б) обычные уравнения материального и теплового балансов для стационарных режимов.

17

2. Уравнения ”элементарных” процессов для локальных потоков:

а) основные кинетические закономерности процесса. Например, для процесса массопередачи:

Для процессов химических реакций можно рассчитывать скорости химических реакций (по уравнению кинетики химической реакции):

ная температура, K ).

б) уравнения, определяющие равновесные состояния процесса (основные термодинамические уравнения).

Например, для процессов ректификации, сушки, экстракции равновесные состояния между жидкостью и газом описыва-

где yi , xi – концентрации i -го компонента в жидкой и газовой фазах соответственно; ki - константа фазового равновесия.

18

Для процесса химической реакции: A B K C D ,

ские соотношения для процессов массопередачи (выводятся из закона Генри (1.6)).

дельных компонентов в газовой фазе равна единице или 100 %).

концентраций компонентов в жидкой фазе также равна единице). Для процессов химических реакций условие стехиометрии:

i 1

где i - стехиометрический коэффициент по i -му компоненту. В сумме со знаком “+” указываются образующиеся компоненты,

асо знаком “-” – исходные компоненты.

3.Неравенства или равенства (ограничения, накладываемые на параметры процесса).

Ограничения вытекают из физической сущности

процессов: 0 xi 1 - концентрация не может быть отрицательна или быть больше единицы (100 %).

1.4. Структура эмпирических моделей

Поскольку функция отклика (взаимосвязь между входными и выходными параметрами) нам неизвестна, в этом случае,

19

основная задача заключается в получении структуры модели (структуры уравнения или группы уравнений).

Если выход объекта зависит от одного входа y f x , а вид зависимости достаточно прост, то характер этой зависимости можно оценить по графику (рис. 1.3) и подобрать соответствующую структуру модели (уравнение прямой, параболы, тригонометрическое или трансцендентное уравнение и т. д.).

Рис. 1.3. График экспериментальной кривой

Если входных воздействий несколько y f x1 , x2 ,..., xk ,

то для определения структуры модели пользуются тем, что практически большинство функций можно разложить в ряд Тейлора.

Если ограничиться несколькими первыми членами ряда, то получим полином (многочлен), являющийся приближенным выражением неизвестной функции.

Рассмотрим выбор структуры модели для объекта с тремя входами и одним выходом (рис. 1.4).

Рис. 1.4. Объект моделирования с тремя входами и одним выходом

20