MS_bak_220400_220700

Продолжение табл. 3.17

161

Окончание табл. 3.17

162

Глава 4. РАЗРАБОТКА И ИССЛЕДОВАНИЕ МОДЕЛИ СТАТИКИ ПРОЦЕССА РЕКТИФИКАЦИИ

В пищевой и химической промышленности значительное место занимают процессы массообмена (ректификации, абсорбции, десорбции, экстракции и т. д.), в которых массообмен происходит между различными фазами. В результате чего достигается обогащение одной из фаз одним или несколькими компонентами смеси. Математическое моделирование процессов используется для их исследования и выбора оптимальных режимных параметров.

Рассмотрим разработку и исследование детерминированной модели на примере процесса ректификации. Необходимо определить концентрации разделяемых компонентов смеси по высоте ректификационной колонны при заданных входных управляющих и возмущающих параметрах. Исследование модели заключается в построении статических характеристик процесса, выборе управляющих параметров и оптимизации процесса по выбранному критерию.

4.1. Состав математического описания процесса и принимаемые допущения к модели

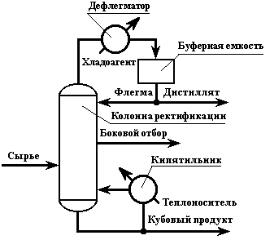
Задачей моделирования процесса ректификации (рис. 4.1) является расчет состава выходных продуктов колонны и концентраций разделяемых компонентов на каждой контактной ступени разделения при заданных значениях входных управляющих и возмущающих параметров [13].

Математическое описание статики процесса ректификации включает следующие группы уравнений:

1. Уравнения материальных балансов колонны в целом, по секциям и каждой контактной ступени разделения по каждому компоненту.

2.Уравнения парожидкостного (фазового) равновесия.

3.Соотношения, устанавливающие кинетику массообмена.

163

4. Ограничения, вытекающие из стехиометрических соотношений.

Рис. 4.1. Схема ректификационной установки

В зависимости от степени детализации модели могут приниматься те или иные допущения. Допустим, примем следующие допущения:

-жидкость на контактных ступенях разделения (тарелках) колонны, а также в кубе и дефлегматоре идеально перемешивается;

-унос жидкости с тарелок паром отсутствует;

-расходы жидкости и пара в потоках по высоте отдельных секций колонны принимаются постоянными;

-пар, покидающий отдельные тарелки колонны находится

вравновесии с жидкостью (рассматривается стационарный процесс);

-весь пар, покидающий последнюю тарелку, полностью конденсируется в дефлегматоре;

-температурный профиль по высоте колонны принимается линейным;

-куб и дефлегматор рассматриваются как теоретические тарелки;

164

-сырье подается в колонну в жидкой фазе;

-боковой погон отбирается в газовой фазе.

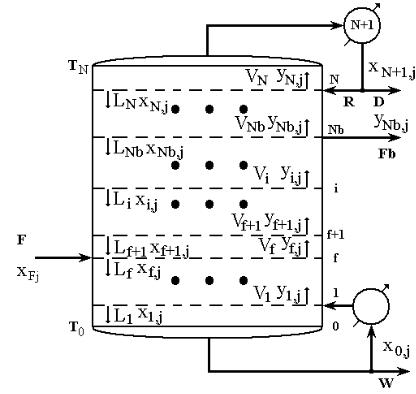
Рассмотрим составление математической модели на примере брагоэпюрационной колонны с боковым отбором фракции в производстве спирта (рис. 4.2).

Рис. 4.2. Схема материальных потоков колонны

Обозначения, принятые на схеме:

F, R, D, Fb,W - расходы сырья, флегмы, дистиллята, бокового отбора и кубового продукта, т/ч;

L,V - расходы жидкости и пара, отходящие с каждой тарелки (контактной ступени разделения), т/ч;

165

x, y - концентрации компонентов смеси в жидкой и газовой фазах, % мас.;

T0 ,TN - температура в кубе и на последней тарелке колон-

ны, С.

Введем нумерацию контактных ступеней разделения (снизу вверх): i - текущий номер ступени; N - общее число ступеней; f - тарелка, на которую подается питание; Nb - тарелка боково-

го отбора; 0 - нулевая ступень (куб колонны); N 1 - дефлегматор.

j- номер компонента разделяемой смеси;

k- общее число компонентов;

X Fj - концентрация j -го компонента в сырье, % мас.;

xi, j , yi, j - концентрации j -го компонента в жидкой и газо-

вой фазах, отходящие с i -той тарелки, % мас.

Для брагоэпюрационной колонны, рассматриваемой в качестве примера, общий материальный баланс по колонне описы-

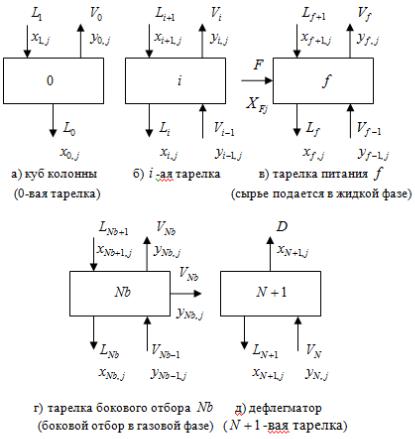
Уравнения покомпонентного материального баланса (рис. 4.3), (4.9) для каждой из тарелок колонны от куба до дефлегматора:

Рис. 4.3. Схемы материальных потоков колонны по тарелкам

167

равновесия систем “жидкость - пар”

При условии фазового равновесия между газом и жидкостью связь составов газовой и жидкой фаз устанавливается уравнением Генри:

ние паров индивидуальных компонентов смеси.

168

В зависимости от компонентов разделяемой смеси и принятых допущений предусматривается шесть алгоритмов расчета констант фазового равновесия:

1) с постоянными коэффициентами j , не зависящими от

температуры;

2) с коэффициентами i, j , зависящими от температуры (температурный профиль – линейный);

3) с коэффициентами i, j , зависящими от температуры че-

рез давление паров индивидульных компонентов (температурный профиль по высоте колонны – линейный);

4) с коэффициентами i, j , зависящими от температуры и

состава смеси (температурный профиль – линейный);

5) с коэффициентами i, j , зависящими от температуры че-

рез давление паров индивидульных компонентов (температурный профиль – нелинейный);

6) с коэффициентами i, j , зависящими от температуры и состава смеси (температурный профиль – нелинейный).

Алгоритм 1

Коэффициенты относительной летучести постоянны:

Алгоритм 2

Коэффициенты относительной летучести зависят от температуры:

постоянные коэффициенты.

Если температурный профиль по высоте колонны принимается линейным, то температуру на любой тарелке можно рассчитать по линейной зависимости:

169

где i - текущий номер тарелки.

- давление паров индивидуального (чистого) компонента, кгс/см2. По алгоритму 3 коэффициенты активности принимаются

го компонента смеси; Ti - значение температуры на i -ой тарелке

(переводится в градусы Кельвина) [14, 15].

Также может использоваться уравнение Антуана:

Алгоритм 4

Коэффициенты относительной летучести определяются по формуле (4.14).

170