
MS_bak_220400_220700
.pdf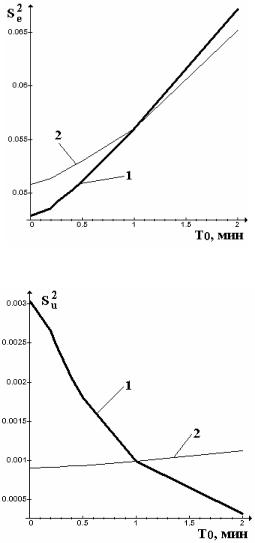
где uN - установившееся значение управляющей переменной на
N -м такте квантования.
Рис. 3.33. Зависимость Se2 от длительности такта T0
Рис. 3.34. Зависимость Su2 от длительности такта T0
141
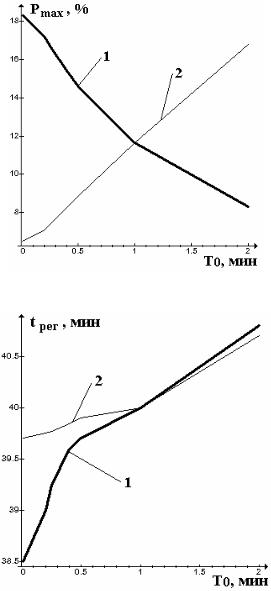
Рис. 3.35. Зависимость Pmax от длительности такта T0
Рис. 3.36. Зависимость t рег от длительности такта T0
142
Таблица 3.16
Параметры дискретной модели объекта, оптимальные настройки цифрового ПИ-регулятора и значения среднеквадратичной ошибки для разных тактов квантования
№ |
T0 , |
a |
1 |
a |
2 |
b , |
d |
qопт , |
q опт , |
S 2 опт |
q пер , |
q пер , |
S 2 пер |
п/п |
|
|
|
2 |
|
0 |
1 |
e |
0 |
1 |
e |
||
мин |
|
|
|
|
С/(т/ч) |
|
(т/ч)/ С |
(т/ч)/ С |
|
(т/ч)/ С |
(т/ч)/ С |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
0,08 |
1,95046 |
-0,96108 |
0,00248 |
25 |
0,39860 |
-0,39545 |
0,04777 |
0,29094 |
-0,28813 |
0,05007 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
0,1 |
1,93863 |
-0,93959 |
0,00383 |
20 |
0,39565 |
-0,39172 |
0,04790 |
0,29094 |
-0,28743 |
0,05086 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
0,2 |
1,88245 |
-0,88607 |
0,01446 |
10 |
0,38022 |
-0,37243 |
0,04862 |
0,29094 |
-0,28216 |
0,05137 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
0,25 |
1,85604 |
-0,86153 |
0,02197 |
8 |
0,37285 |
-0,36317 |
0,04912 |
0,29094 |
-0,28216 |
0,05164 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
0,4 |
1,78246 |
-0,79545 |
0,05194 |
5 |
0,35258 |
-0,33736 |
0,05023 |
0,29094 |
-0,27689 |
0,05245 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
0,5 |
1,73745 |
-0,75675 |
0,07722 |
4 |
0,34039 |
-0,32160 |
0,05112 |
0,29094 |
-0,27337 |
0,05300 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
7 |
1,0 |
1,54658 |
-0,60869 |
0,24844 |
2 |
0,29094 |
-0,25581 |
0,05599 |
0,29094 |
-0,25581 |
0,05599 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
8 |
2,0 |
1,25892 |
-0,43750 |
0,71428 |
1 |
0,22632 |
-0,16521 |
0,06715 |
0,29094 |
-0,22067 |
0,06319 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
143
В табл. 3.16 для различных значений такта T0 представле-
ны параметры дискретной модели объекта и настройки цифрового ПИ-регулятора, рассчитанные двумя способами: градиентным
методом оптимизации - настройки q0опт , q1опт (графы 7, 8) и по формулам пересчета - настройки q0пер , q1пер (графы 10, 11), а так-
же соответствующие им значения показателя Se2 (графы 9 и 12). Установлено, что существует связь между зависимостями
основных показателей качества Se2 , t рег от T0 (рис. 3.33, 3.36)
при оптимизации настроек цифрового регулятора и при их пересчете. Поэтому при изменении такта квантования сигналов при эксплуатации ЦСУ, реализованных на управляющих микропроцессорных контроллерах и не обладающих мощными вычислительными средствами, можно воспользоваться пересчетом настроек цифровых регуляторов для новых тактов T0 . Однако при наличии достаточно мощных вычислительных средств, используемых в управлении, предпочтительней оптимизировать настройки цифровых регуляторов при изменении T0 .
Характер зависимостей других важнейших показателей S e2 и Su2 от такта T0 (рис. 3.33, 3.34) противоположный. Совмещая эти зависимости (рис. 3.37) и устанавливая весовой коэффициент
r , получаем комплексный критерий |
S 2 |
(3.96), |
по экстремуму |
||||||
|
|
|
|
|
eu |
|
|
|
|
которого выбирается оптимальный такт |
T0 |
и соответствующие |
|||||||
ему оптимальные настройки q0 , q1 (рис. 3.38). |
|
|
|||||||
|
|
1 |
|
N |
|
|
|
|
|
Seu2 |
|
|
ei2 |
r ui2 , |
(3.96) |
||||
|
|
|
|||||||
N |
|
|
|||||||
|
mc i mc |
|
|
|
|
|
|||
где ei - ошибка управления; |
ui - отклонение управляющей пе- |
||||||||
ременной от установившегося значения ui |
ui |
uN . |
|
||||||
144 |
|
|
|
|
|
|
|
|
|

Рис. 3.37. Зависимости показателей S e2 и Su2 от такта T0
Рис. 3.38. Зависимость комплексного критерия Seu2
от длительности такта T0 при разных весовых коэффициентах r
145
Для расчета весового коэффициента r , который определяет требования к точности управления и одновременно к затратам на управление, рекомендуется воспользоваться формулой, полу-
ченной в результате исследования влияния величины r |
на харак- |
|||||
тер зависимости S 2 |
f T : |
|
|
|
|
|
eu |
0 |
|
|
|
|
|
|
r 0,15 0,4 S 2 |
S 2 |
|
T 0 |
, |
(3.97) |
|
|
|||||
|
e |
u |
|
|
|
|
|
|
|
|
0 |
|
|
где T 0 - начальный выбранный такт. |
|
|
|
0 |
|
|
|
По зависимости на рис. 3.38 для синтезированной ЦСУ по- |
|||
лучен оптимальный такт T опт =0,5 мин и соответствующие ему |
|||
|
0 |
|
|
оптимальные |
настройки |
qопт =0,34039 |
(т/ч)/ С, |
|
|
0 |
|
q1опт =-0,3216 (т/ч)/ С цифрового ПИ-регулятора.
Для сокращения объема вычислений можно проводить оптимизацию такта и настроек регулятора по выбранному комплексному критерию (3.96) методом покоординатного спуска. Следует отметить, что расчет T0 при синтезе ЦСУ может осуще-
ствляться для объектов без запаздывания ( 0 ) без жестких требований по величине начального такта T00 с учетом извест-
ных ограничений. При 0 рекомендуется начальный T00 выбирать небольшим для уменьшения погрешности при пересчете числа тактов запаздывания d дискретной модели объекта, либо проводить оптимизацию настроек регулятора только при таких значения T0 , когда отношение  T0 равно целому числу.
T0 равно целому числу.
Проведенное исследование позволяет выбрать такт квантования T0 , обеспечивающий минимальное значение выбранного
комплексного критерия.
Для снижения объема вычислений при пересчете параметров дискретных моделей объекта и регулятора с новым j-тым тактом квантования T0 получены следующие формулы (для мо-
делей объекта 1-го, 2-го порядков и ПИ-, ПД-, ПИД-регуляторов):
146
при n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
a j 1 T j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T j |
T j 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
a j |
|
|
|
|
1 |
0 |
|
|
|
0 |
|
|
0 |
|
, |
|
|
|
|
|
|
(3.98) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b j |
|
b j 1T0j |
d j |
|
d j 1T j 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
0 |
|
; |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
T j 1 |
|
|
|
|
|
T0j |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
при n 2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a j |
a1j 1 T0j 2 a2j 1 T0jT0j 1 2 T0j 1 2 T0j 2 |
T0jT0j 1 T0j 2 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
a2j 1 T0jT0j 1 |
T0j 1 2 T0jT0j 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
a2j |
|
|
|
|
|
|
|
|
|
a2j 1 T0j 1 2 |
|
|
|
|
|
|
|
, |
|
(3.99) |
||||||||||||||||
|
|
|
|
|
a2j 1 T0jT0j 1 |
T0j 1 2 T0jT0j 1 |
|
||||||||||||||||||||||||||||||||||
b j |
|
|
|
|
|
|
b j 1 |
T0j 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
d j 1T j 1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, d j |
|
|
0 |
|
; |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
T0 |
j 1 2 |
|
|
|
|
|
|
|
|
|
|
j |
|
|
|||||||||||||||||
|
|
|
|
|
j 1 |
|
|
j |
j 1 |
|
|
|
j |
|
|
j 1 |
|
|
|
|
|
|
|
T0 |
|
|
|
|
|||||||||||||
|
|
|
|
a2 |
T0 |
T0 |
|
|
|
|
|
|
|
T0 |
T0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
для ПИ-регулятора |
|
|
|
|
|
|
|
|
q j 1 T j |
T j 1 q j 1T j |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
q j |
q j 1 |
, |
|
q j |
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
1 |
|
0 |
; |
(3.100) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T j 1 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для ПД-регулятора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
q0j 1 |
T0j |
q1j 1 T0j 1 T0j |
|
|
|
|
q j 1T j 1 |
|
|
|
|
||||||||||||||||||||||||||
|
|
q j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
q j |
|
1 |
|
0 |
; (3.101) |
|||||||||
|
|
|
|
|
|
|
|
|
|
T j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T j |
||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
для ПИД-регулятора |
|
|
|
|
q j 1T j q j 1 T j 1 |
T j |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
q j |
|
0 |
0 |
|
|
|
2 |
|
|
|
|
0 |
|
|
|
0 |
|
, |
|
|
|
(3.102) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T j |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
T0j 2 T0jT0j 1 |
q1j 1 T0j |
|
|
0 |
|
|
|
|
T0j 2 T0jT0j 1 2 T0j 1 2 |
|||||||||||||||||||||||||||||
q j |
q0j 1 |
2 q2j 1 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T jT j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q j |
q2j 1T0j 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
T j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
147 |
|||
3.14. Контрольные вопросы
1.Какие преимущества имеют цифровые системы перед аналоговыми?
2.Как преобразовать непрерывную форму сигнала в дискретную?
3.Как осуществляется переход от непрерывных динамических моделей к дискретным?
4.Чем обусловлен выбор начальных условий для расчета переходных процессов по разностным уравнениям?
5.Провести расчет переходного процесса динамического звена по разностному уравнению (на примере моделей 1-го-3-го порядков).
6.Получить дискретные передаточные функции с помощью оператора сдвига z (на примере разностных уравнений 1-го- 3-го порядков).
7.Каким методом проводится параметрическая идентификация дискретной динамической модели?
8.Как оценить адекватность модели реальному объекту по критерию Фишера?
9.Привести примеры объектов со связанными входными и выходными параметрами.
10.Какую информацию об объекте нужно иметь для получения дискретной модели объекта?
11.Как составляется дискретное динамическое описание объекта управления для каскадных, комбинированных и систем с перекрестными связями?
12.Привести примеры дискретного описания объектов со связанными параметрами (для каскадных, комбинированных и систем с перекрестными связями).
13.Как получить дискретное описание регулятора по непрерывной модели (на примере П-, И-, ПИ-, ПД-, ПИДрегуляторов)?
148
14.Какова взаимосвязь настроек непрерывных и цифровых регуляторов (вывод формул взаимосвязи)?
15.Вывести ограничения на настройки цифровых регуляторов для реализации типовых непрерывных законов регулирования (на примере П-, И-, ПИ-, ПД-, ПИДрегуляторов).
16.Провести расчет переходного процесса цифрового регулятора (на примере П-, И-, ПИ-, ПД-, ПИДрегуляторов)?
17.Назвать этапы синтеза одноконтурной цифровой системы регулирования.
18.Записать критерии оптимизации настроек цифровых регуляторов.
19.Как составить систему уравнений для расчета динамических характеристик в одноконтурной системе регулирования (на примере ПИрегулятора и модели объекта 2-го порядка с запаздыванием)?
20.Как получить рекуррентные выражения для расчета частных производных (на примере ПИрегулятора и модели объекта 2-го порядка с запаздыванием)?
21.Составить схему алгоритма оптимизации настроек цифрового регулятора методом градиента (на примере ПДрегулятора и модели объекта 1-го порядка).
22.Как выполняется оптимизация настроек цифрового регулятора по критерию минимум времени регулирования методом покоординатного спуска (на примере ПИ-, ПДрегуляторов и модели объекта 2-го порядка)?
23.Для каких объектов применяются адаптивные системы управления? Принцип работы адаптивной системы.
24.Назвать методы синтеза каскадной цифровой системы регулирования по критерию минимум интегрально-квадратичной ошибки.
25.Составить систему разностных уравнений для расчета динамических характеристик по заданию в каскадной системе (на
149
примере ПИрегуляторов и моделей объекта 3-го порядка с запаздыванием).
26.Составить рекуррентные выражения для расчета частных производных в каскадной системе (на примере ПИрегуляторов и моделей объекта 1-го порядка с запаздыванием)?
27.Как используется метод свертки для расчета цифрового регулятора внешнего контура каскадной системы?
28.Назвать этапы синтеза комбинированной цифровой системы регулирования.
29.Составить систему уравнений для расчета динамических характеристик замкнутой комбинированной системы (на примере П- компенсатора, ПИрегулятора и моделей объекта 2- го порядка с запаздыванием)?
30.Как проводиться оптимизация настроек цифрового регулятора и компенсатора по критерию минимум интегральноквадратичной ошибки в комбинированной системе?
31.Как выполняется синтез цифрового компенсатора возмущения из условия инвариантности в комбинированной системе?
32.Перечислить этапы расчета системы несвязанного регулирования объекта с двумя связанными параметрами.
33.Составить систему уравнений для расчета динамики несвязанной системы регулирования (на примере ПИрегуляторов
имоделей объекта 2-го порядка с запаздыванием).
34.Назвать этапы синтеза связанной системы регулирова-
ния.
35.Как составить систему уравнений для расчета динамических характеристик связанной системы регулирования (на примере ПИрегуляторов и моделей объекта 2-го порядка с запаздыванием)?
36.Назвать основные способы расчета цифровых связанных систем регулирования.
150
