MS_bak_220400_220700

где yN - значение выхода объекта на N -ном такте (установив-

шееся значение).

При наличии статической ошибки (статические регуляторы) расчет показателей качества (3.89) - (3.92) проводится с учетом этой ошибки, т. е. показатели вычисляются по выходу объек-

та yi относительно установившегося значения yN y3 y , а

не по значению задания y 3 . Например, расчет времени регули-

рования можно выполнять по формуле (3.55).

Расчет показателей качества позволяет судить не только об эффективности системы управления, но и обоснованно выбирать структуры регуляторов и сравнивать варианты схем управления для конкретного технологического объекта, т. е. проводить синтез структуры управляющей части ЦСУ.

Например, при синтезе каскадной системы управления (рис. 3.13) сначала из различных структур оптимизируемых регуляторов внутреннего контура выбирается регулятор, при оптимальных настройках которого значение критерия оптимизации минимально, а другие показатели не превышают заданных ограничений. Затем для выбранной структуры и рассчитанных настроек регулятора внутреннего контура выполняется оптимизация настроек цифрового регулятора внешнего контура (для различных структур, например, табл. 3.4). Выбор регулятора проводится аналогично.

При расчете комбинированной системы (рис. 3.17) проводится структурный и параметрический синтез регулятора по основному каналу, а затем вычисляются настройки компенсатора различных структур оптимизационным методом по критерию (3.79) или из условия инвариантности. Эффективность системы оценивается сравнением показателей качества комбинированной и одноконтурной схем управления при нанесении воздействия по каналу возмущения (например, импульсного (рис. 3.19)). Выбор же компенсатора осуществляется на основе анализа показателей качества для различных структур.

131

Качество работы несвязанной системы управления (рис. 3.21) определяется при сравнении с одноконтурными схемами, в которых расчет регуляторов выполнялся по основным каналам без учета перекрестных связей (рис. 3.23).

При синтезе систем связанного управления (рис. 3.25) исследуются показатели качества, вычисляемые для различных способов расчета основных и компенсирующих регуляторов (последовательная и одновременная оптимизация регуляторов, расчет компенсаторов из условия автономности (рис. 3.27)). По показателям качества выбирается наиболее эффективная структура управления объектом со связанными параметрами.

3.12. Исследование чувствительности систем управления к нестационарному поведению объектов

Расчет оптимальных настроек цифровых регуляторов при разработке ЦСУ осуществляется по дискретному описанию объекта управления, получаемому в результате идентификации экспериментальных динамических характеристик, которые с течением времени могут изменяться, что обусловлено нестационарностью объектов.

Возникновение дрейфа динамических характеристик технологических объектов в процессе их нормальной эксплуатации связано с различными факторами (например, для процессов ректификации углеводородов - это коррозия металла, вызывающая образование свищей на тарелках колонны, налипание полимера на внутренних стенках теплообменников, изменение селективности экстрагента и т. д.). Изменение характеристик вызывает несоответствие модели объекту, что требует уточнения параметров

иструктуры модели.

Врезультате синтезируемый по модели оптимальный алгоритм цифрового управления с постоянными настройками может не обеспечить высокого качества управления на объекте в условиях дрейфа характеристик.

Кроме того, оценка эффективности различных вариантов синтезированных схем ЦСУ может не позволить выявить струк-

132

туру ЦСУ, обеспечивающую наилучшее качество управления по сравнению с другими вариантами, т. к. рассчитанные показатели качества могут быть достаточно близкими между собой, что требует дополнительных способов исследования разработанных систем.

Поэтому помимо расчета показателей качества управления дополнительно исследуется чувствительность разработанных ЦСУ к дрейфу динамических характеристик объектов, что позволяет оценивать эффективность функционирования синтезированных систем в реальных условиях.

В случае разработки различных вариантов схем ЦСУ данное исследование позволяет выявлять оптимальные структуры систем управления с позиции устойчивости к нестационарному поведению объектов управления.

Оценка чувствительности представлена на примере исследования одноконтурной ЦСУ концентрацией бутиленов в дистилляте ректификационной колонны [6].

Модель ЦСУ описывается системой уравнений (3.46). Параметры a1 , a2 ,b, d дискретной модели объекта получены по экспериментальной динамической характеристике с помощью МНК. По параметрам a1 , a2 ,b, d рассчитаны постоянные времени T1 , T2 , коэффициент усиления k и время чистого запаздывания объекта (табл. 3.2). Настройки q0 , q1 цифрового регулято-

ра 1-го порядка оптимизированы градиентным методом оптимизации по критерию (3.45). По найденным оптимальным настройкам q0 , q1 определены настройки k p , Tиз непрерывного ПИ-

регулятора (табл. 3.5). Результаты вычислений представлены в табл. 3.13.

Для имитации дрейфа динамики объекта последовательно изменялись параметры дискретной модели a1 , a2 ,b, d в пределах0,1 5 % от их исходных значений, определяемых на этапе идентификации, и рассчитывалась величина выбранного критерия – среднеквадратичной ошибки (3.94). Такое на первый взгляд незначительное изменение параметров дискретной модели объ-

133

В результате исследований устанавливается диапазон вариаций параметров a1 , a2 ,b, d (с учетом возможного дрейфа ха-

рактеристики объекта), при котором значение критерия S e2 из-

меняется в пределах 0,02 2,6 % от наилучшего (минимального) значения (рис. 3.29).

При таком диапазоне изменения S e2 другие показатели качества (время регулирования, перерегулирование и т.д.) изменялись в допустимых для ведения процесса пределах. Установлены следующие диапазоны изменения параметров дискретной модели объекта и соответствующие им диапазоны изменения параметров непрерывной модели, при которых в пересчете настроек q0 , q1 цифрового ПИ-регулятора нет необходимости, т. к. обеспечива-

T2 =10,44 13,01 мин, k =0,277 0,161 %/(т/ч)); для b 5 % ( k =0,193 0,213 %/(т/ч)); для d 3 7 тактов ( =6 14 мин).

Рис. 3.29. Изменение критерия S e2 в диапазоне 0,02-2,6 %

от вариаций параметров a1 , a2 , b дискретной модели

Из рис. 3.29 видно, что наибольшее увеличение критерия S e2 вызывает изменение параметра a1 . Поясним более подробно

получение зависимости Se2 f a1 .

На рис. 3.30 представлены переходные характеристики объекта при изменении параметра a1 дискретной модели.

135

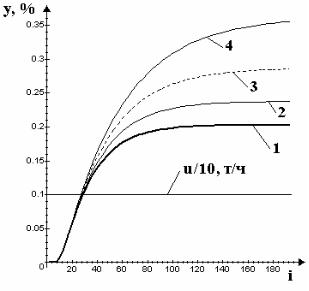
Рис. 3.30. Переходные характеристики объекта при исходном значении параметра a1 (кривая 1) и при его увеличении на 0,05 % - (кривая 2), на 0,1 % - (кривая 3), на 0,15 % - (кривая 4) от исходного значения

Если для параметров a1 , a2 дискретной модели 2-го порядка выполняется ряд ограничений ( a1 >0, a2 <0, a1 >| a2 |, a1 + a2 <1, 1+ a2 >0) для расчета параметров непрерывной модели по табл. 3.2, то при изменении параметра a1 одновременно будут изменяться параметры T1 ,T2 , k непрерывной модели (табл. 3.14).

Т. к. оптимальные настройки q0 , q1 цифрового ПИ-

регулятора рассчитаны для исходной модели объекта (табл. 3.13), то изменение динамической характеристики объекта (рис. 3.30) приведет к ухудшению качества управления (рис. 3.31), оценен-

ного зависимостью Se2 f a1 (рис. 3.32).

136

Установленная зависимость не линейна: при увеличении параметра a1 в диапазоне 0,1 % от исходного значения (кривая 3, которой соответствует 53 %-ное увеличение постоянной времени T1 , 8 %-ное уменьшение постоянной времени T2 и 42 %-ное

увеличение коэффициента усиления k0 ) критерий S e2 увеличивается незначительно (рис. 3.32), дальнейшее изменение a1 при-

водит к достаточно резкому увеличению критерия (кривая 4), а при 0,2 %-ном увеличении - система становится неустойчивой.

Представленная методика исследования чувствительности синтезированной ЦСУ к дрейфу динамической характеристики объекта (путем изменения параметров дискретной модели и вычисления критерия управления) позволяет выбирать структуры регуляторов и схемы управления, наименее чувствительные к нестационарному поведению объекта.

137

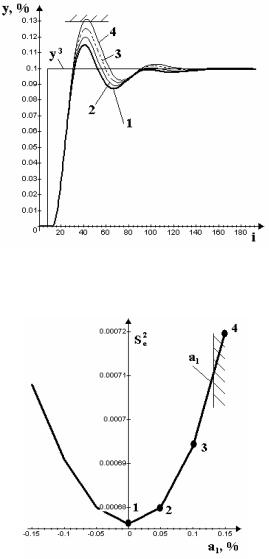
Рис. 3.31. Динамические характеристики ЦСУ при увеличении задания регулятору концентрации бутиленов в дистилляте на 0,1 % при исходном (кривая 1) и измененных (кривые 2,3,4) значениях параметра a1

Рис. 3.32. Зависимость критерия S e2 от изменения параметра a1 дискретной динамической модели объекта в диапазоне

0,15 % от номинального значения

138

3.13. Исследование влияния длительности квантования сигналов в системах на качество управления

Особенностью цифровых систем является наличие квантования сигналов. Квантование может проводиться по уровню сигналов и по времени. Наиболее распространенным является квантование по времени. Поэтому в отличие от непрерывных в цифровых системах управления всегда присутствует важный параметр - длительность такта квантования сигналов. Определение оптимального (рационального) такта квантования такая же важная задача при синтезе системы цифрового управления, как и расчет настроек регуляторов, т. к. его величина влияет на качество работы системы. Следует отметить, что расчет такта необходимо проводить с учетом ограничений по времени выполнения вычислительных операций и из теоремы Котельникова-Шеннона.

Для оптимизации такта квантования T0 наряду с настройками цифровых регуляторов при синтезе ЦСУ необходимо установить характер зависимостей между длительностью такта T0 и

показателями качества управления с целью формирования критерия, обеспечивающего проведение этой процедуры.

Например, установлен характер влияния длительности такта T0 на показатели качества при синтезе ЦСУ температурой

смеси в кубе колонны экстрактивной ректификации изопентанизоамиленовой фракции [6]. Экспериментальная динамическая характеристика объекта по каналу «расход теплоносителя - температура смеси в кубе колонны» идентифицирована дискретной моделью 2-го порядка ( n 2 ) с помощью МНК при такте квантования T0 =1 мин (табл. 3.15). По полученным параметрам

a1 , a2 ,b, d рассчитаны параметры T11 ,T22 , k, непрерывной модели (табл. 3.2).

139

диапазоне 0,08 2 мин. При этом для каждого выбранного из указанного диапазона такта T0 пересчитывались параметры

a1 , a2 ,b, d дискретной модели объекта (3 6 графы в табл. 3.16) по полученным формулам (табл. 3.1) и проводилась оптимизация настроек q0 , q1 цифрового ПИ-регулятора по критерию (3.45)

(кривые 1).

Кривыми 2 на рис. 3.33 – 3.36 представлены аналогичные зависимости, но в этом случае оптимизация настроек q0 , q1 проводилась только при исходном такте T0 =1 мин. Значения настроек q0 , q1 (10,11 графы в табл. 3.16) при других тактах определя-

лись пересчетом по оптимальным, найденным при исходном такте (по формулам из табл. 3.6, 3.5).

Зависимости получены для среднеквадратичной ошибки (3.94), среднеквадратичного отклонения управляющей переменной от установившегося значения (3.95), величины перерегулирования (3.91) и времени регулирования (3.90).

140