MS_bak_220400_220700

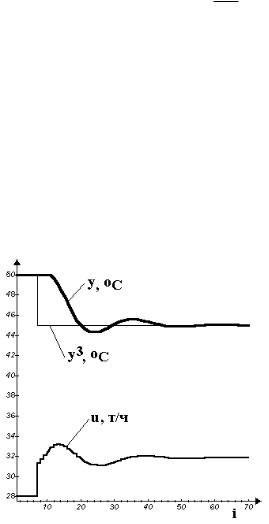
( yi3 yi3 yн , yi yi yн , ui ui uн , i 1, N , где uн , y н -

начальные значения параметров, при которых наносилось ступенчатое воздействие).

Рис. 3.10. Динамические характеристики оптимальной одноконтурной ЦСУ температуры на верхней контрольной тарелке колонны

ректификации: y 3 - задание по температуре; y - температура (выход); u - расход флегмы (управляющее воздействие)

92

Другим важнейшим критерием качества является время регулирования (3.55).

где tрег - время, в течении которого выход объекта yi достигает 95 98 % от нового установившегося значения выхода yN при

изменении задания y 3 ( tрег i* T0 , где i * - номер такта, для которого выполняется проверяемое условие при изменении i от N

Оптимизацию по критерию минимум времени регулирования рассмотрим на примере модели одноконтурной системы (3.46). Для определения оптимальных настроек q0 ,q1 регулятора

1-го порядка воспользуемся методом покоординатного спуска, т. к. аналитический вид критерия (3.55) записать нельзя.

После расчета динамических характеристик замкнутой системы и критерия S0 (3.55) при начальных заданных настройках регулятора, по первой настройке q0 выполняется пробный шаг в

где 0 k1 1, 1 k2 2 .

Затем осуществляется шаг по первой настройке q0 в направлении убывания критерия:

94

После этого аналогично выполняется шаг по второй настройке q1 и т. д.

Расчет считается законченным, когда величина шага по каждой настройке становиться меньше заранее заданной величины , которая характеризует окрестность определения оптимума

Расчет динамических характеристик одноконтурной ЦСУ в ходе оптимизации проводится по системе уравнений (3.46) при нулевых начальных условиях.

Если требуется выполнить расчет одного из непрерывных регуляторов (табл. 3.6), то необходимо учитывать ограничения на его настройки. Кроме того, при поиске оптимума критерия может вводится дополнительное ограничение (например, динамическая ошибка не должна превышать 5 15 % от установившегося значения). Эти требования учитываются в ходе оптимизации добавлением соответствующих ограничений.

Например, после расчета шага по каждой настройке проверяются ограничения на соответствие непрерывному закону (табл. 3.6) и если они не выполняются, то рассчитанные значения настроек не принимаются в качестве нового приближения к оптимуму. В этом случае оптимальное значение критерия будет определено на границе с ограничениями.

3.6. Синтез адаптивной цифровой системы управления с настраиваемой моделью

Для управления различными технологическими процессами широко используют типовые схемы стабилизации. Однако их применение оказывается малоэффективным для нестационарных технологических объектов, у которых наблюдается плавное или

95

скачкообразное изменение характеристик. Для таких объектов целесообразно применение адаптивных цифровых систем управления (АЦСУ). Реализация адаптивных систем на средствах вычислительной техники требует достаточно сложной проработки математического и программного обеспечения.

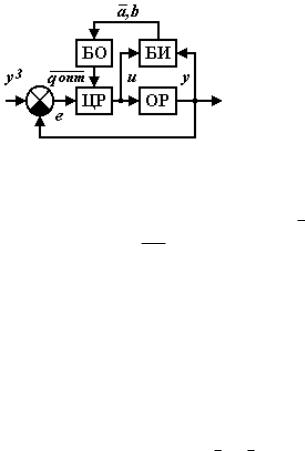
Структурная схема АЦСУ с настраиваемой моделью выглядит следующим образом (рис. 3.11).

Рис. 3.11. Структурная схема АЦСУ:

ЦР – цифровой регулятор; ОР – объект регулирования; БИ – блок текущей идентификации параметров модели ОР; БО – блок оптимизации

настроек ЦР; y 3 – задающее воздействие; e – величина рассогласова-

ния; u – управляющее воздействие; y – регулируемый параметр; a, b

– параметры настраиваемой модели ОР; qопт – оптимальные настройки ЦР

Для описания системы используются дискретные динамические модели:

l 0

n

yi ak yi k b ui d 1 , k 1

где ui , yi – выходы ЦР и объекта на i -ом такте квантования T0 ;

m, n - порядки регулятора и модели объекта; q и a, b, d – их параметры.

96

Текущая адаптация параметров a, b в БИ может прово-

диться одним из рекуррентных методов. Например, рекуррентным методом наименьших квадратов (РМНК) на основе измере-

k 1

Расчет оптимальных настроек qопт в БО осуществляется на каждом такте численным градиентным методом (по адаптируемым параметрам модели объекта a, b ) по выбранному критерию (см. пункт 3.5). Значения настроек qопт передаются в ЦР для

расчета управляющего воздействия u на следующем такте квантования. Таким образом, осуществляется оптимальная подстройка регулятора по адаптируемым параметрам модели объекта (при изменении свойств нестационарного объекта).

Разберем получение формул адаптации (3.60) при использовании РМНК на примере дискретной динамической модели 2- го порядка с запаздыванием (получим формулу уточнения пара-

Для модели (3.61) критерий МНК определяется выражени-

ем:

97

Находим первую производную по искомому параметру модели a1 и раскрываем скобки:

N

a2 yN 1 yN b ui 1 d yi 1 b u N d yN .

i 1

Прибавим к левой и правой части уравнения (3.63) слагаемое a1N yN2 :

N

b ui 1 d yi 1.

i 1

Вычтем из левой и правой части уравнения (3.64) соответственно левую и правую части уравнения (3.65):

98

дущих тактах, а также измерять текущие значения yN , yN 1 , uN d .

Чтобы знаменатели формул (3.67) – (3.69) не стремились к бесконечности необходимо ограничивать число запоминаемых зна-

99

чений (вводится параметр Nn ) и обеспечивать “забывание” информации на предыдущих тактах (3.60).

3.7. Синтез каскадной системы цифрового управления методами декомпозиции и свертки по критерию минимум интегрально-квадратичной ошибки

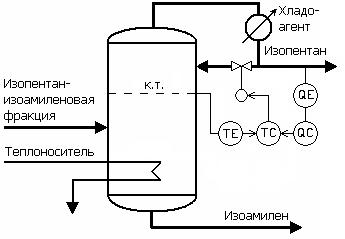
Каскадные системы управления (рис. 3.12, 3.13) применяются для технологических объектов, в которых можно выделить промежуточный управляемый параметр. При этом более быстродействующий внутренний контур компенсирует внешние воздействия на объект еще до изменения основного управляемого параметра. Это обеспечивает высокое качество управления такими объектами при правильной настройке регуляторов.

Рис. 3.12. Пример каскадной системы управления температурой на верхней контрольной тарелке (к.т.) колонны ректификации с коррекцией по концентрации изоамиленов в дистилляте:

ТЕ, QE – датчики температуры, состава; ТС – регулятор температуры (внутренний контур); QC – корректирующий регулятор состава (внешний контур)

100