
2 Асимптоты функций.
Определение
4. Прямая
![]() называется вертикальной асимптотой
графика функции
называется вертикальной асимптотой
графика функции![]() ,
если выполняется хотя бы одно из
соотношений:
,
если выполняется хотя бы одно из
соотношений:
1)![]() или 2)
или 2)![]() .
.
Таким образом, чтобы найти вертикальные асимптоты графика функции, надо проверять точки, в которых функция терпит разрыв, а также границы области определения.
Пример
3. Найти асимптоты кривой
![]() .
.
Решение.
Находим точки разрыва функции:
![]() .
.
Находим пределы слева и справа от этой точки:
![]() ;
; ![]() .
.
Следовательно,
![]() --- вертикальная асимптота.
--- вертикальная асимптота.
Определение
5. Прямая
![]() называется наклонной асимптотой графика
функции
называется наклонной асимптотой графика
функции![]() ,
если
,
если
![]() (
(![]() ).
).
Таким
образом, наличие асимптоты у графика
функции означает, что расстояние от
точки
![]() графика до асимптоты стремиться к нулю,
когда точка
графика до асимптоты стремиться к нулю,
когда точка![]() удаляется в бесконечность.
удаляется в бесконечность.
Теорема
5. Для того,
чтобы график функции
![]() имел наклонную асимптоту
имел наклонную асимптоту![]() ,
необходимо и достаточно, чтобы существовали
и были конечными пределы
,
необходимо и достаточно, чтобы существовали
и были конечными пределы
![]()
![]() (5)
(5)
(![]()
![]() ).
).
Пример.
Найти асимптоты кривой.![]() .
.
Решение.
1) Найдем вертикальные асимптоты. Функция
терпит разрыв при
![]() .
Вычислим пределы:
.
Вычислим пределы:
![]()
![]() .
.
Поэтому
прямая
![]() есть вертикальная асимптота.
есть вертикальная асимптота.
2) Найдем наклонные асимптоты.:
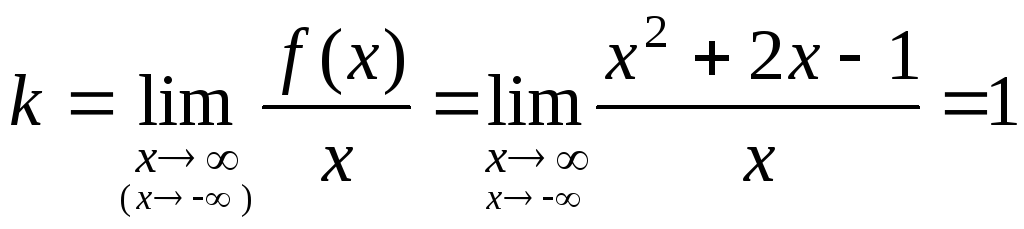
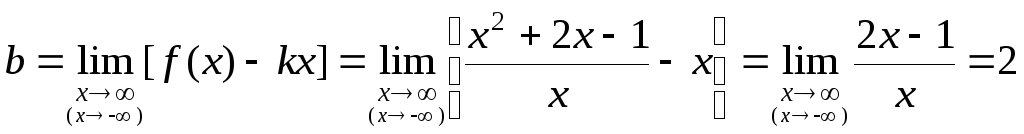 .
.
Таким
образом, прямая
![]() --- наклонная асимптота данной кривой
как при
--- наклонная асимптота данной кривой
как при![]() ,
так и при
,
так и при![]() .
.
3. Общая схема исследования функции и построение ее графика.
Укажем
теперь схему действий, которую надо
проделать при исследовании функции
![]() и построения ее графика:
и построения ее графика:
найти область допустимых значений;
определить точки разрыва функции;
исследовать функцию на четность-нечетность и периодичность (наличие этих свойств упрощает построение графика);
если возможно, решить уравнение
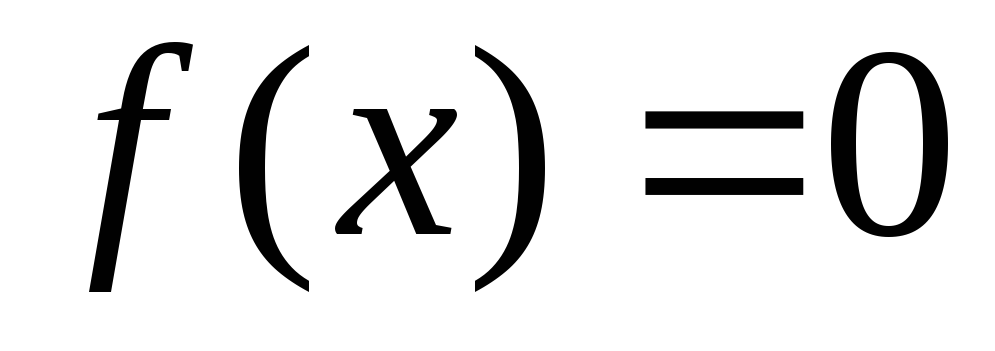 и тем самым найти точки пересечения с
осьюOX
(y=0),
а затем интервалы, на которых функция
не меняет знак;
и тем самым найти точки пересечения с
осьюOX
(y=0),
а затем интервалы, на которых функция
не меняет знак;определить интервалы возрастания и убывания функции и найти точки экстремума;
найти интервалы выпуклости и вогнутости и точки перегиба;
найти асимптоты графика функции.
Пример
5. Исследовать функцию
![]() и построить ее график.
и построить ее график.
Решение.
1)
область допустимых значений:
![]() ;
;
2)
![]() --- точка разрыва:
--- точка разрыва:
3)
![]() ;
;
и
![]() ,
то есть функция не является ни четной,
ни нечетной.
,
то есть функция не является ни четной,
ни нечетной.
Функция непериодическая.
точки пересечения с осью OX:
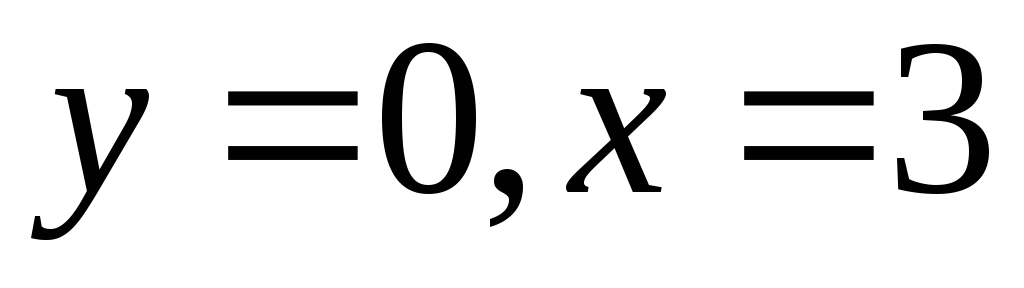 ,
то есть кривая пересекает ось OX
в точке (3,0);
,
то есть кривая пересекает ось OX
в точке (3,0);
точки
пересечения с осью OY:
![]() ,
то есть кривая пересекает осьOY
в точке
,
то есть кривая пересекает осьOY
в точке
![]() .
.
5)Для определения интервалов монотонности и нахождения экстремумов найдем производную первого порядка:
![]()
Стационарные
точки:
![]() и точка
и точка![]() ,
в которой производная не существует (в
ней не определена и сама функция),
разбивают область определения на четыре
интервала. Определим знак производной
на каждом из получившихся интервалов:
,
в которой производная не существует (в
ней не определена и сама функция),
разбивают область определения на четыре
интервала. Определим знак производной
на каждом из получившихся интервалов:
при
![]()
![]() ,
следовательно, на этом интервале функция
возрастает;
,
следовательно, на этом интервале функция
возрастает;
при
![]()
![]() ,
следовательно, функция убывает;
,
следовательно, функция убывает;
при
![]()
![]() ,
следовательно, функция убывает;
,
следовательно, функция убывает;
при
![]()
![]() ,
следовательно, функция возрастает.
,
следовательно, функция возрастает.
Так
как производная меняет знак при
прохождении через точку
![]() с плюса на минус, то точка (-1,-2) --- точка
максимума. Так как при прохождении
через точку
с плюса на минус, то точка (-1,-2) --- точка
максимума. Так как при прохождении
через точку![]() производная меняет знак с минуса на
плюс, то точка
производная меняет знак с минуса на
плюс, то точка![]() --- точка минимума.
--- точка минимума.
Для определения интервалов выпуклости и вогнутости, и точек перегиба находим производную второго порядка
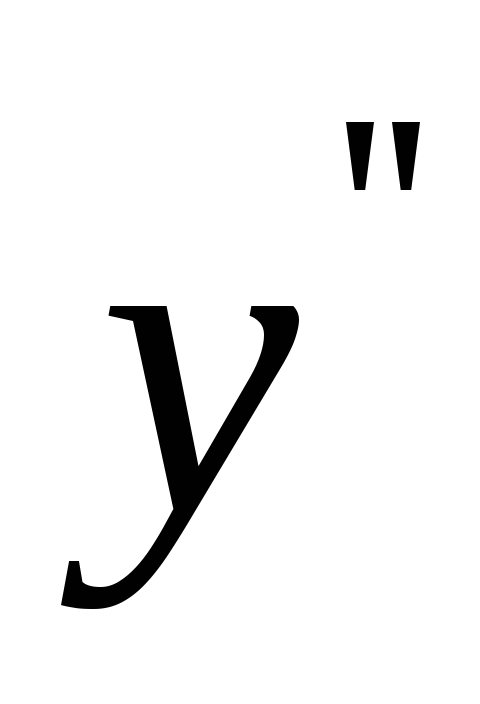 :
:
![]() ;
;
![]() ,
откуда следует, что
,
откуда следует, что
![]() при
при![]() и
и![]() при
при![]() .
.
Таким
образом, на интервале
![]() функция вогнута, а на интервале
функция вогнута, а на интервале![]() функция выпуклая. Точек перегиба нет,
так как
функция выпуклая. Точек перегиба нет,
так как![]() не входит в ОДЗ.
не входит в ОДЗ.
Найдем асимптоты графика функции:
а)
![]() вертикальная асимптота --- вертикальная
асимптота, так как
вертикальная асимптота --- вертикальная
асимптота, так как
![]() ,
,
![]() .
.
б) наклонные асимптоты:
при
![]()
![]() ,
, ![]() =
=![]()
![]() .
.
Таким
образом, прямая
![]() --- асимптота при
--- асимптота при![]() .
Нетрудно показать, что эта же прямая
есть асимптота при
.
Нетрудно показать, что эта же прямая
есть асимптота при![]() .
.
Пример исследования и построения приведён в методическом указании к выполнению контрольной работы № 2.
