- •И.В. Сабаев, г.Н. Егорова
- •Основы начертательной геометрии
- •1.2.1.Свойства параллельной проекции
- •1.3. Ортогональная проекция
- •3.1.Положение прямой относительно плоскостей проекций
- •3.2.Способы преобразования чертежа
- •3.2.1.Способ вращения
- •3.2.2.Способ перемены плоскостей проекций
- •4.1.Способ вращения
- •4.2.Способ перемены плоскостей проекций
- •4.3.Взаимное расположение двух прямых
- •Параллельные прямые
- •4.4.Ортогональная проекция прямого угла
- •5.1.Положение плоскости относительно плоскостей проекций
- •5.2.Прямая и точка в плоскости
- •6.1.Определение натуральной величины плоской фигуры
- •7.2.Параллельность плоскостей
- •7.3.Перпендикулярность прямой и плоскости
- •8.1.Пересечение двух плоскостей
- •9.1.Пересечение гранных поверхностей проецирующими плоскостями
- •9.2.Пересечение тел вращения проецирующей плоскостью
- •9.3.Кривые второго порядка
- •Сабаев Игорь Витальевич егорова Галина Николаевна
- •394000 Воронеж, пр. Революции, 19
9.1.Пересечение гранных поверхностей проецирующими плоскостями
Для определения фигуры сечения, достаточно найти точки пересечения ребер и граней тела с данной плоскостью. Из чертежа видны все построения точек сечения пирамиды проецирующей плоскостью, определение натуральной величины фигуры сечения и ребер пирамиды для построения развертки.
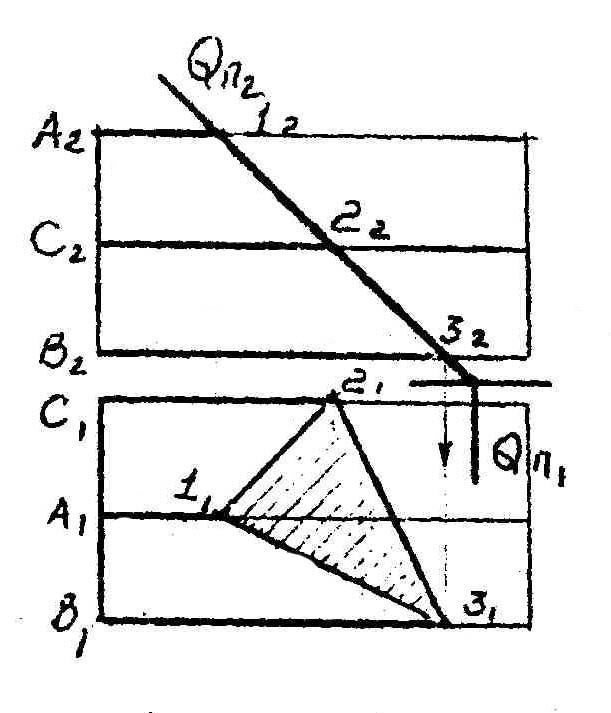
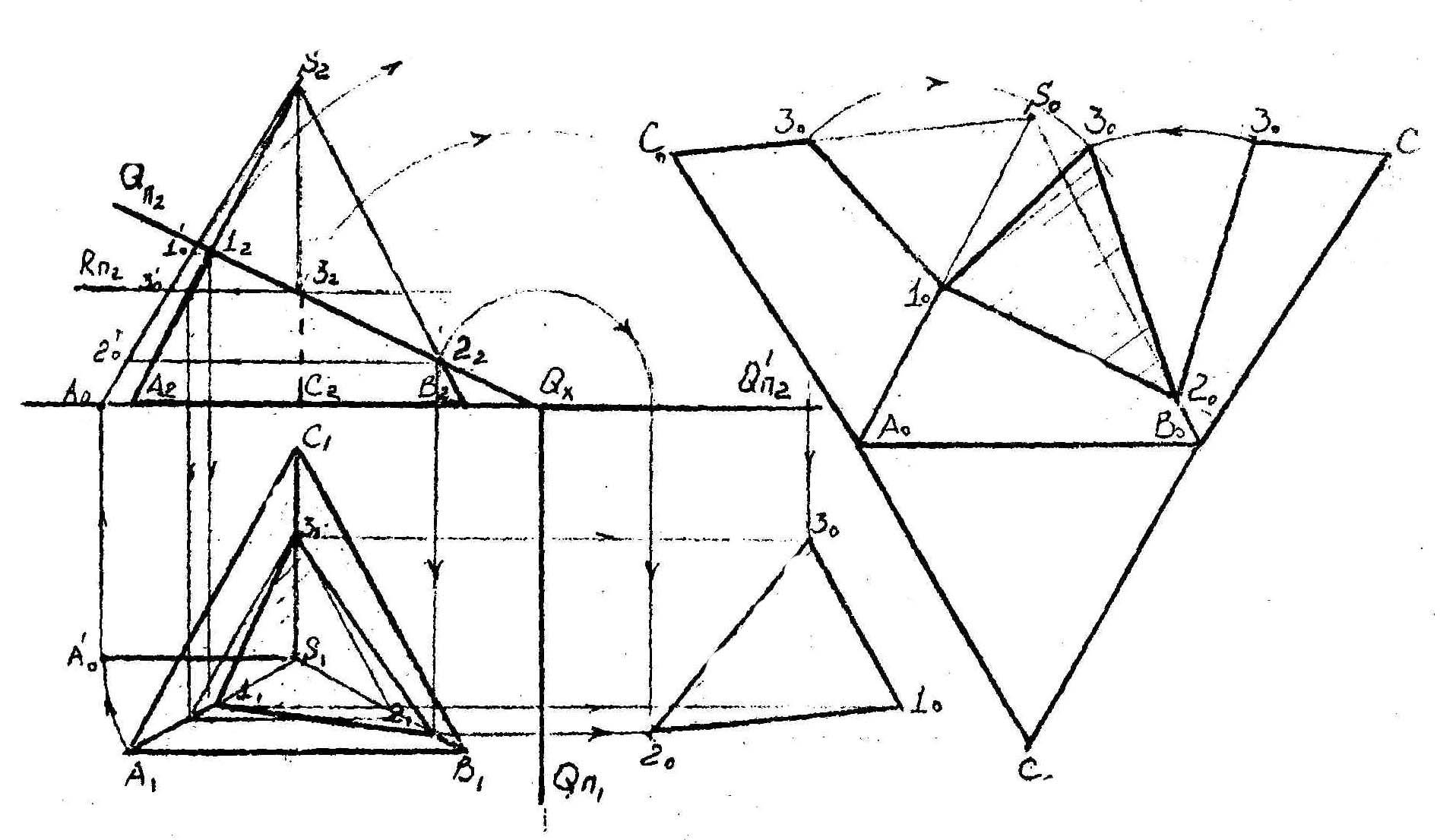
9.2.Пересечение тел вращения проецирующей плоскостью
Пересечение цилиндрической поверхности плоскостью
На чертеже показано построение сечения, определение натуральной величины эллипса и развертки усеченной части цилиндра.
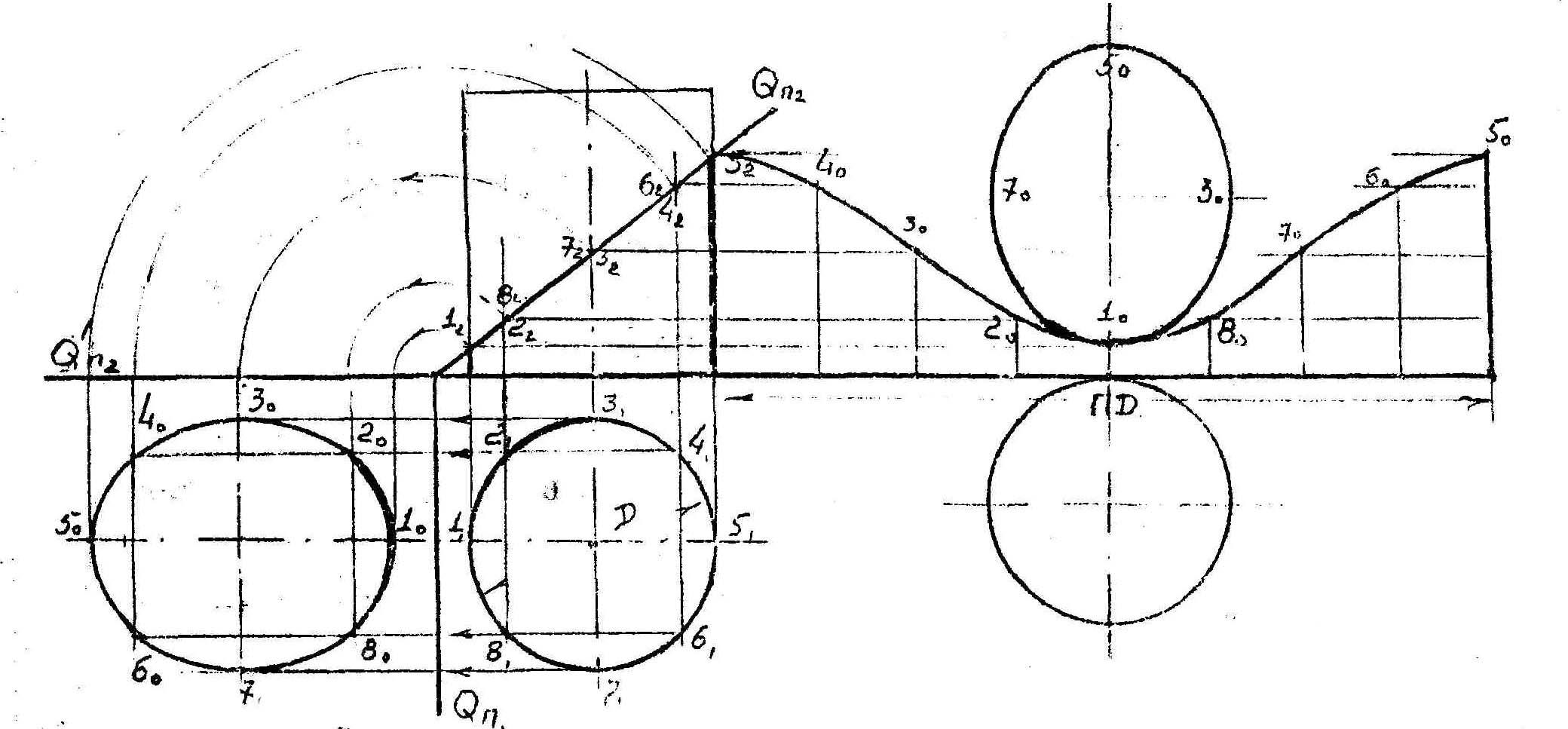
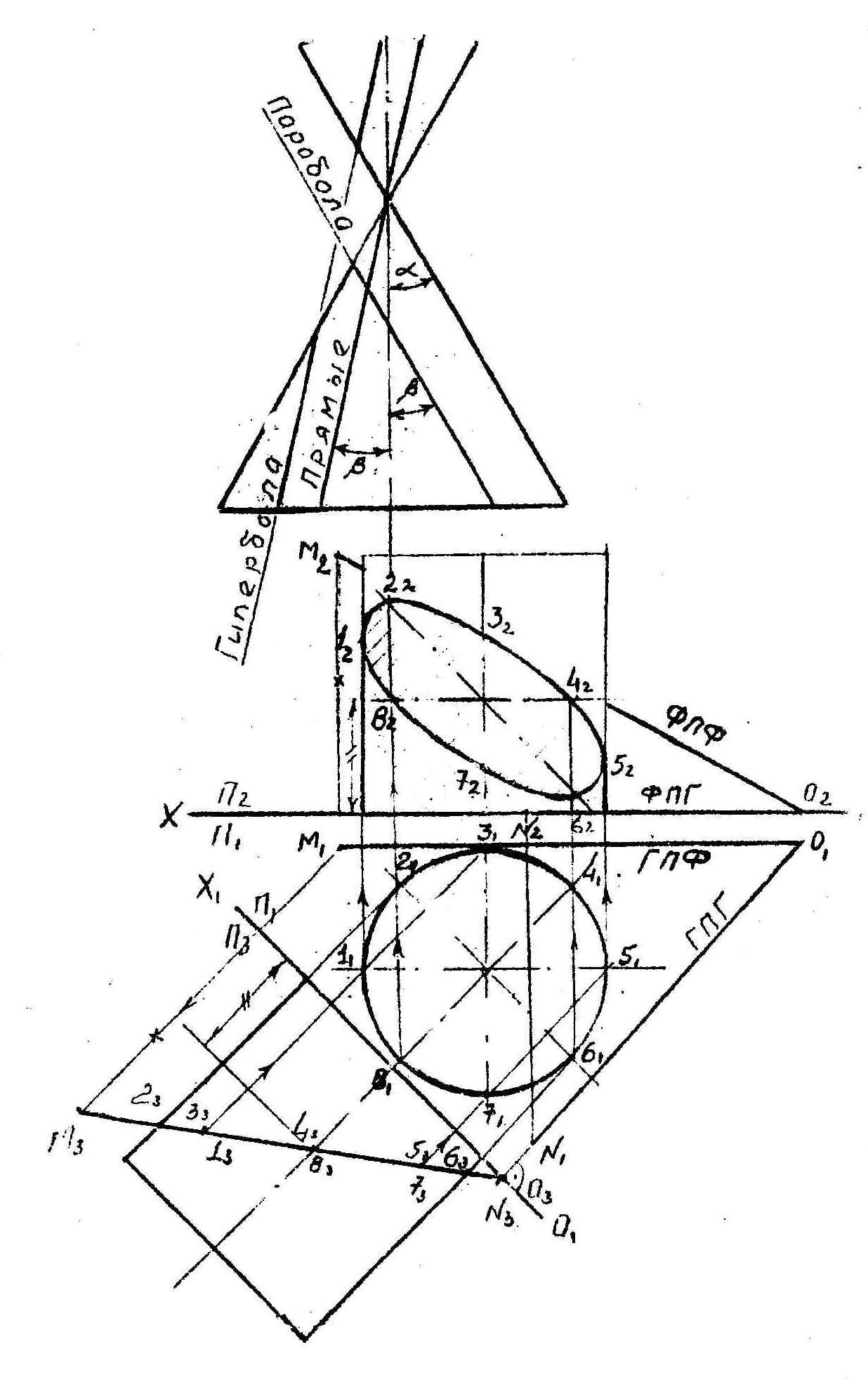
Пересечение конической поверхности плоскостью.Построение развертки
Для получения сечения большую ось эллипса 1-2 делим пополам, проводим через эту точку вспомогательную секущую плоскость и находим положение малой оси эллипса 3-4.
Дальнейшее построение натуральной величины сечения и развертки усеченной части ясно из чертежа.
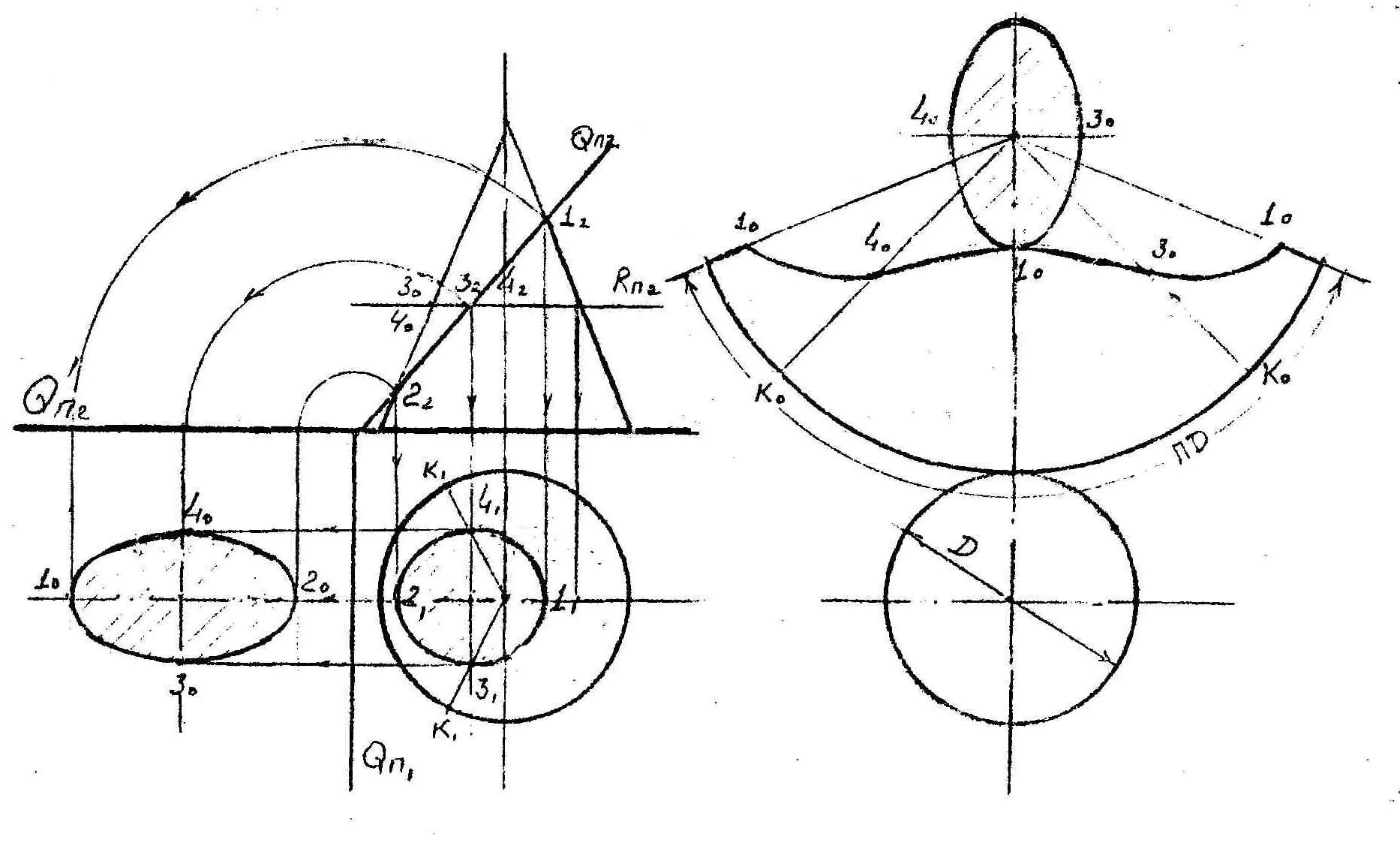
9.3.Кривые второго порядка
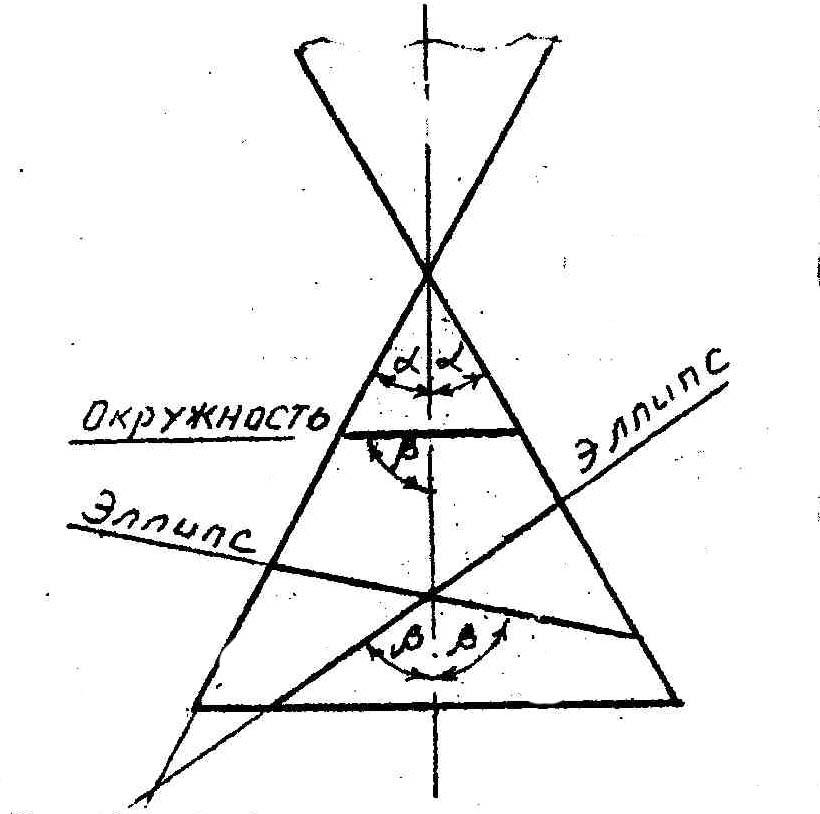
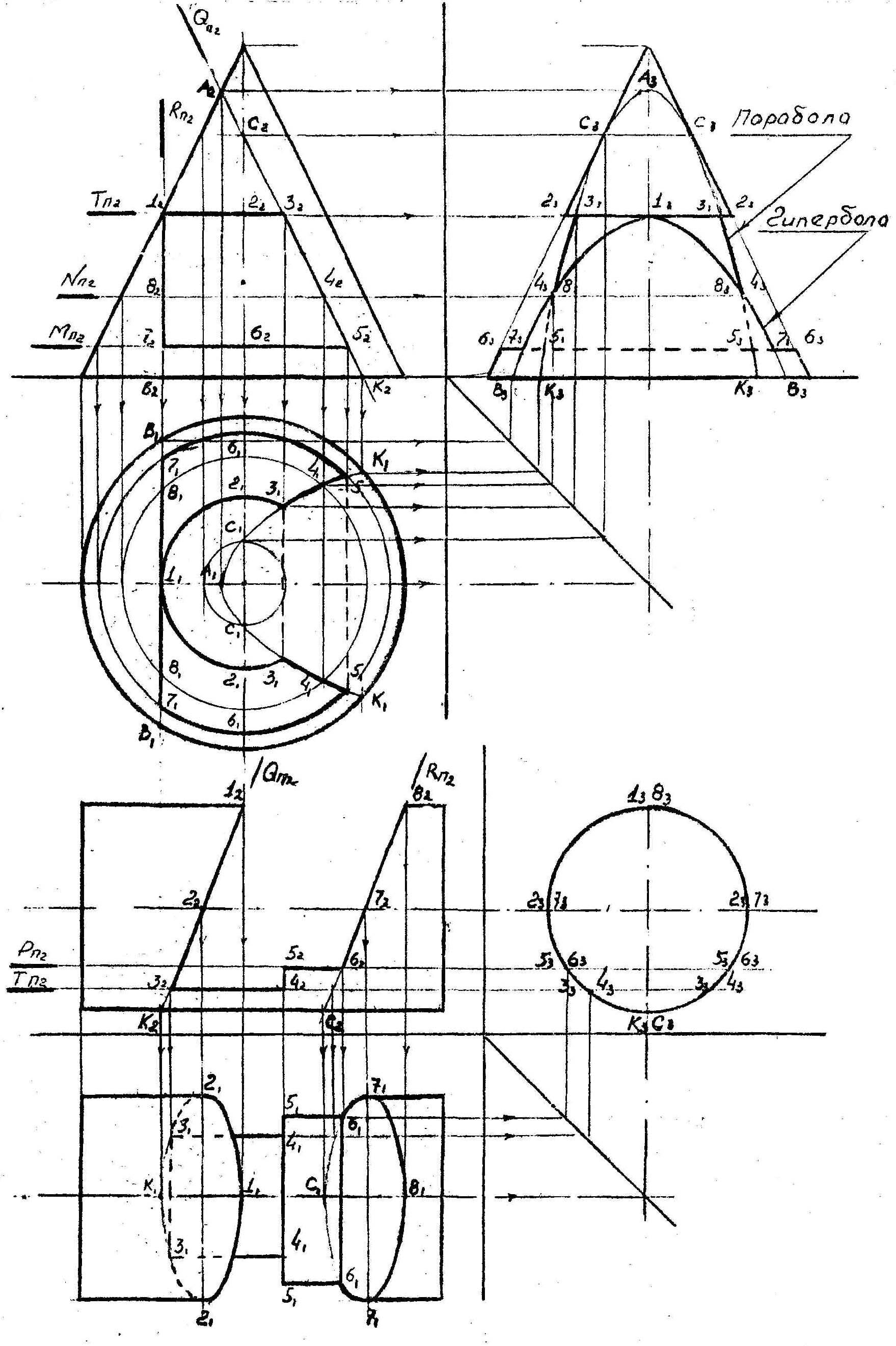
Рассмотрим так называемые конические сечения –кривые второго порядка (окружность, эллипс, парабола и гипербола), широко применяемые в науке и технике.
Без доказательств приводим чертежи и следующие положения:
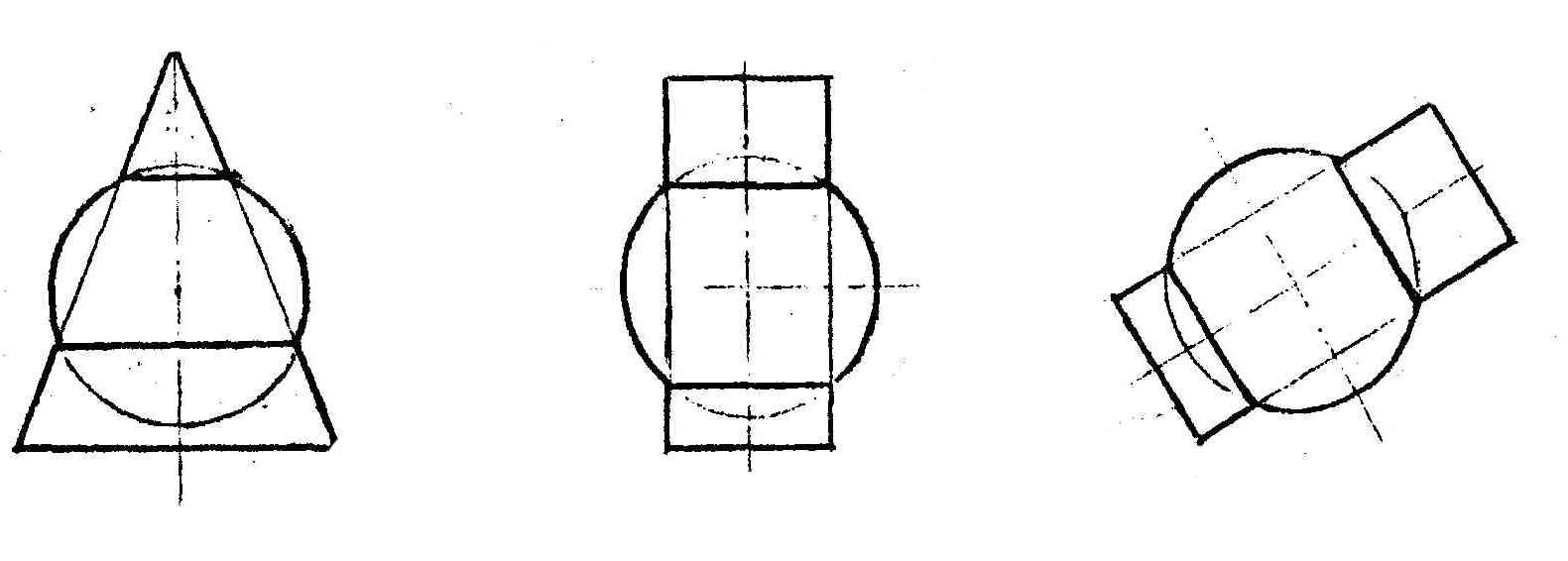
Если пересечь прямой круговой конус плоскостью, параллельной его основанию, – в сечении получим окружность (= 900).
Если пересечь конус плоскостью, не параллельной ни одной из его образующих – в сечении получим эллипс (>).
Если пересечь конус плоскостью, параллельной одной из его образующих, – в сечении получим параболу (=).
Если пересечь конус плоскостью,параллельной двум его образующим (в частном cлучае параллельно его оси),– в сечении получим гиперболу (<).
П ри
пересечении тел плоскостями общего
положения решение намного упрощается,
если путем преобразования чертежа
перейти к новому изображению, когда
плоскость становится проецирующей.
ри
пересечении тел плоскостями общего
положения решение намного упрощается,
если путем преобразования чертежа
перейти к новому изображению, когда
плоскость становится проецирующей.

Лекция 11.ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ГЕОМЕТРИЧЕСКИМИ ПОВЕРХНО-
СТЯМИ.ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙ
Для построения точек пересечения прямой с какой–либо поверхностью следует:
провести через прямую вспомогательную (проецирующую) плоскость;
найти сечение поверхности плоскостью;
определить точки пересечения прямой с контуром сечения (точки входа и выхода);
определить видимость прямой.
|
|
|
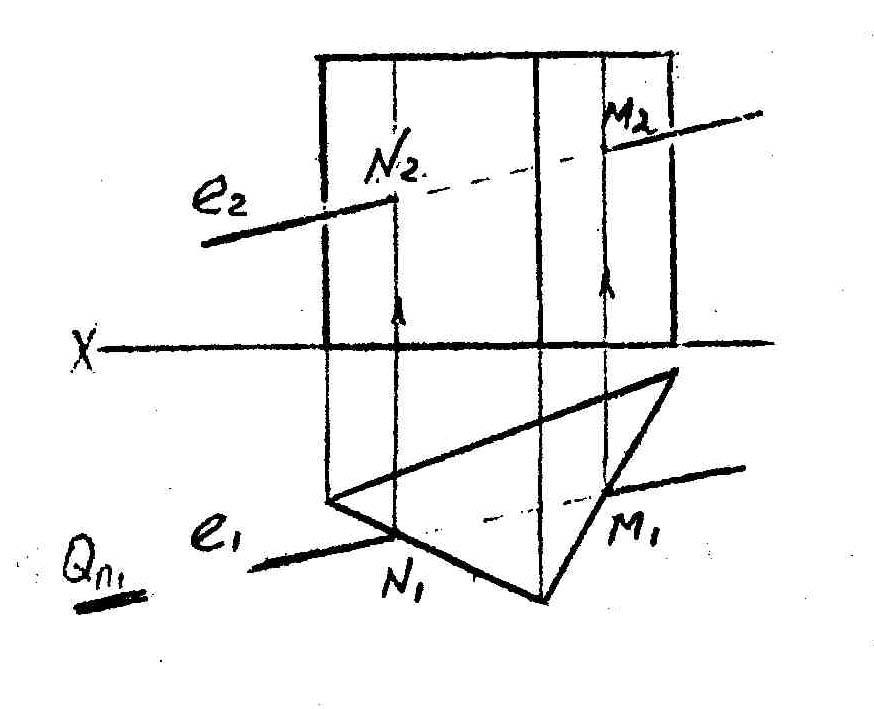
П ри
решении последней задачи для определения
вспомогательного сечения лучше всего
преобразовать чертеж так, чтобы в сечении
получалась окружность, с помощью которой
и находятся искомые точки входа (N) и
выхода (М).
ри
решении последней задачи для определения
вспомогательного сечения лучше всего
преобразовать чертеж так, чтобы в сечении
получалась окружность, с помощью которой
и находятся искомые точки входа (N) и
выхода (М).
При решении задач на определение линий пересечения гранных поверхностей следует определить:
точки пересечения ребер первой поверхности с гранями второй;
точки пересечения ребер второй поверхности с гранями первой;
видимость точек и соединить их прямыми согласно видимости и положению точек на гранях тела.
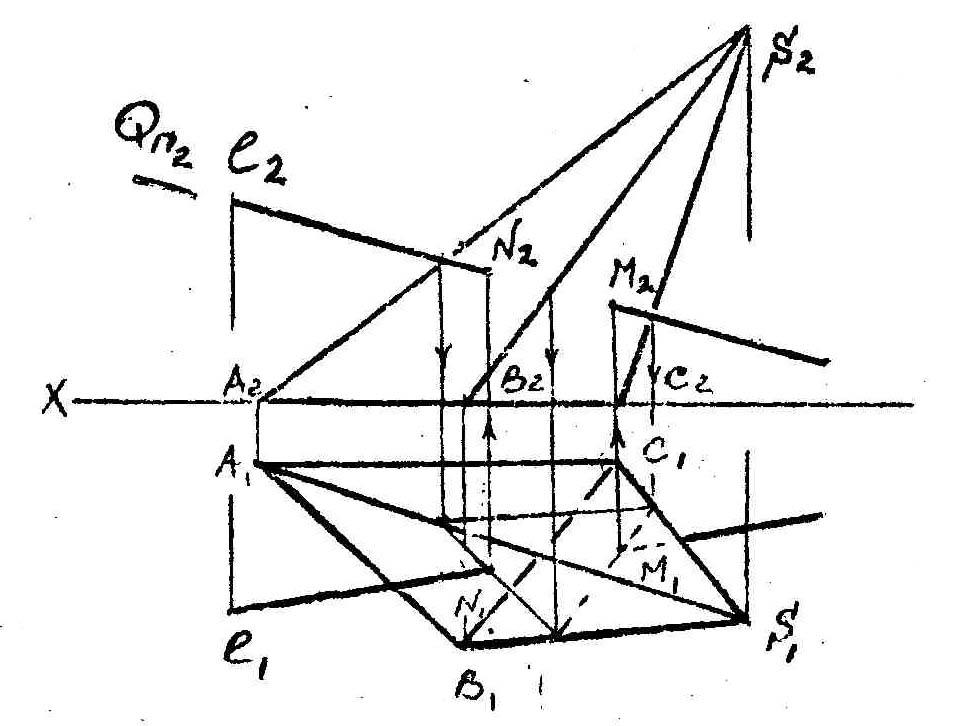
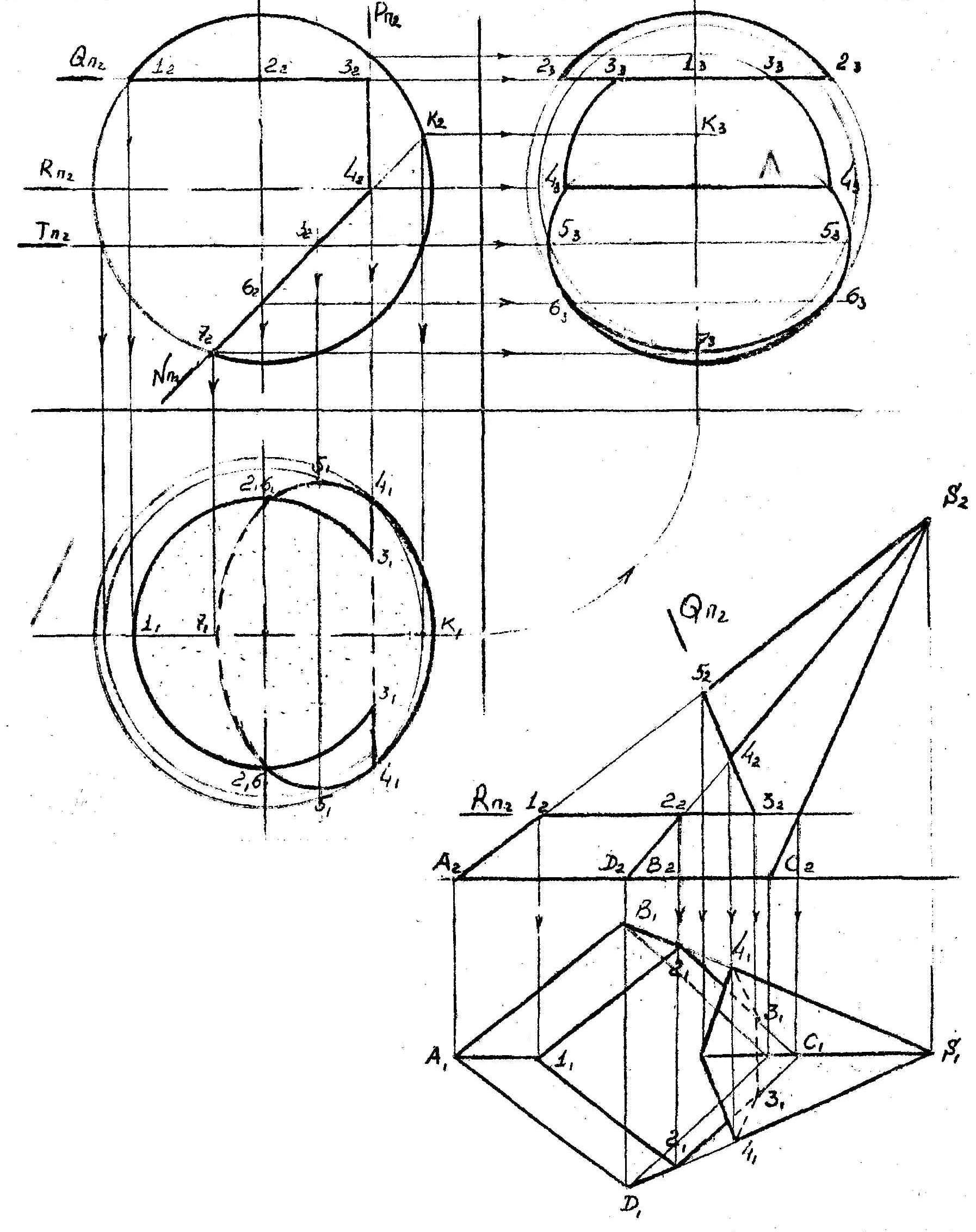
В первом примере легко определяются точки пресечения ребер пирамиды с гранями призмы, т.к. последние являются проецирующими плоскостями. Из ребер призмы с гранями пирамиды пересекается только ребро D.
Заключив его в горизонтально проецирующую плоскость Q, проходящую и через вершину S, получим в сечении треугольник SKN, на границах которого и лежат точки 7 и 8.
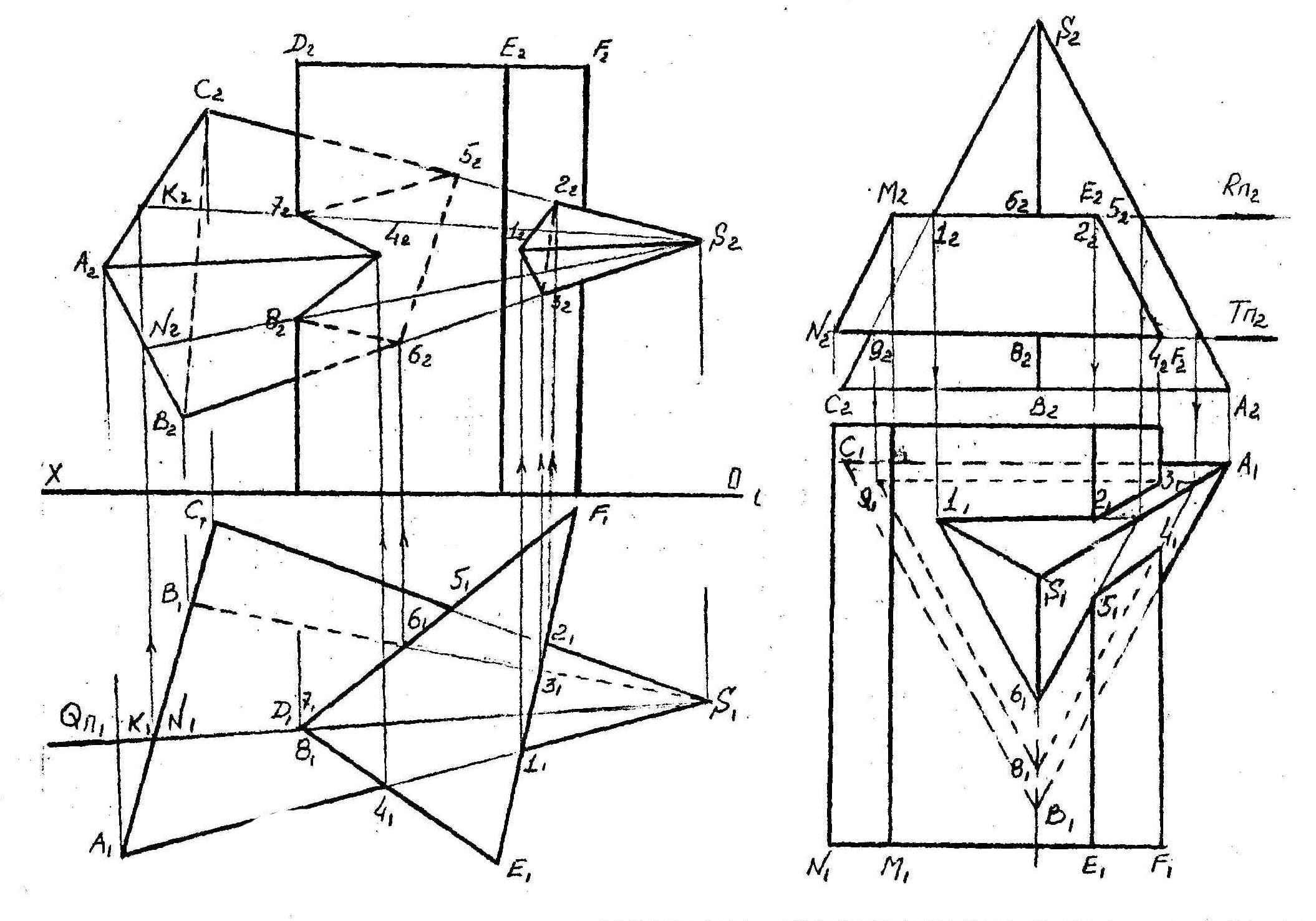
Во втором примере достаточно провести секущие плоскости R и Т и определить точки встречи ребер призмы с вспомогательными сечениями (точки 3 и 4; 2 и 5).
Попутно легко определяются и точки пересечения ребер пирамиды с гранями призмы (точки 6 и 8; 1 и 9).
Лекция 12. ПЕРСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
Способ секущих плоскостей
При решении задач на определение линий пересечения поверхностей вращения следует:
ввести вспомогательную проецирующую плоскость, пересекающую оба тела и дающую «удобные» сечения каждой из поверхностей;
найти общие точки сечений;
с учетом видимости точек провести линию пересечения этих поверхностей.
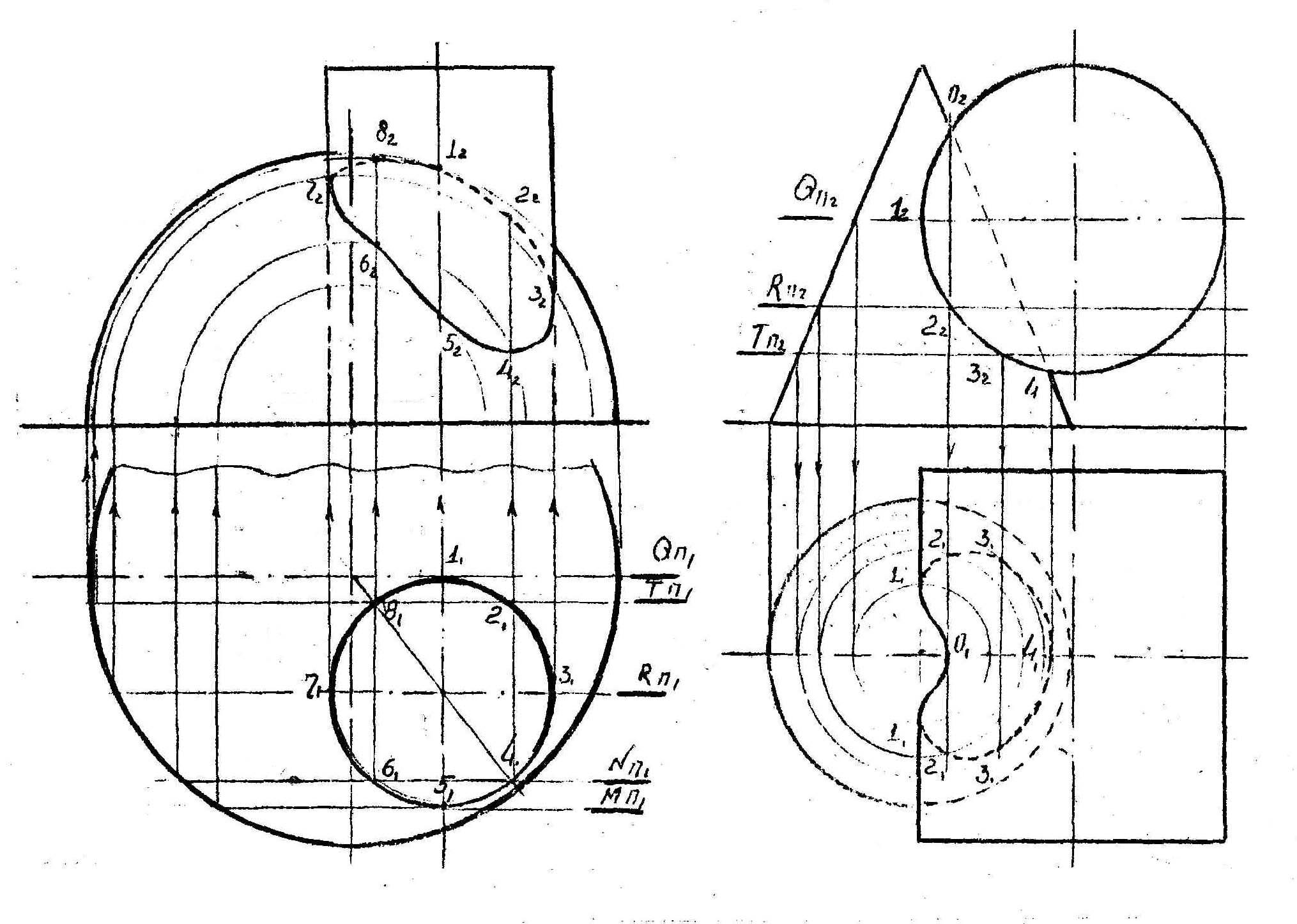
В первом примере использованы фронтальные плоскости проекций,«дающие» в сечении шара окружности и в сечении цилиндра – прямоугольники. Определены левая и правая крайние точки (7 и 3), передняя и задняя (5 и 1) и низшая и высшая (4 и 8).
Во втором примере использованы горизонтальные плоскости проекций, «дающие» в сечении конуса окружности и в сечении цилиндра– прямоугольники. Построение линии пересечения ясно из чертежа.
Способ сфер
Способ сфер применяется при построении линии пересечения поверхностей вращения при условии, что оси поверхностей пересекаются и параллельны одной из плоскостей проекций. В основу способа положено свойство сферы пересекать поверхность по окружности, когда сфера имеет свой центр, расположенный на оси поверхности вращения. Линия пересечения поверхностей будет изображаться на одной из плоскостей проекций в виде прямой, перпендикулярной к оси вращения тел.
В данном примере для определения линии пересечения конуса с цилиндром использованы две концентрические сферы, с помощью которых и определены общие точки, принадлежащие поверхностям вращения.
В частных случаях, когда два тела вращения описаны около одной сферической поверхности, пересечение происходит по двум плоским кривым – эллипсам, проецирующимся на заданную плоскость в виде прямых.
Лекции 13,14.ИЗОБРАЖЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ВЫРЕЗАМИ
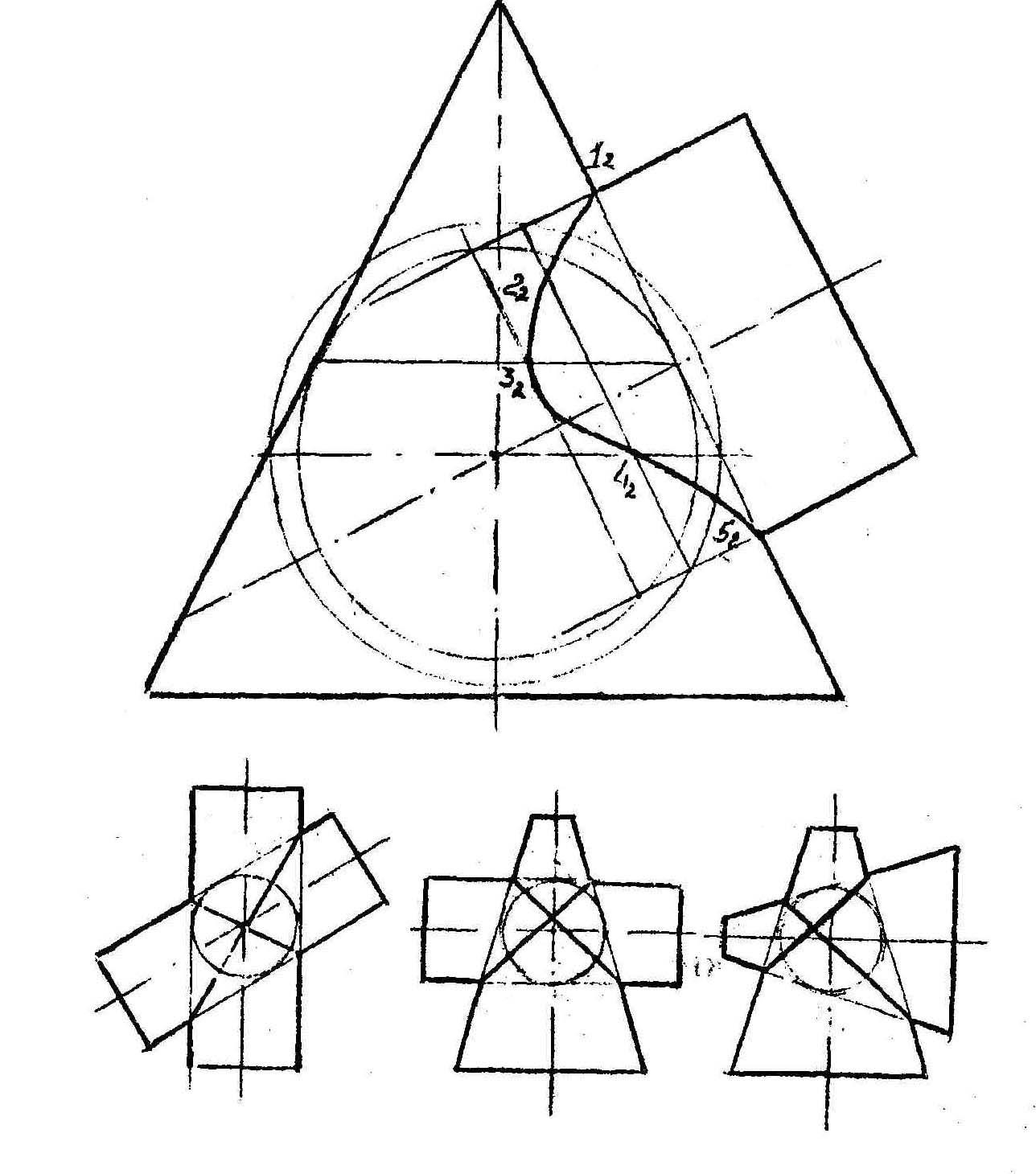
Решение задач на построение тел с вырезами сводится к определению линий пересечения геометрических тел проецирующими плоскостями и хорошо развивает пространственное воображение.
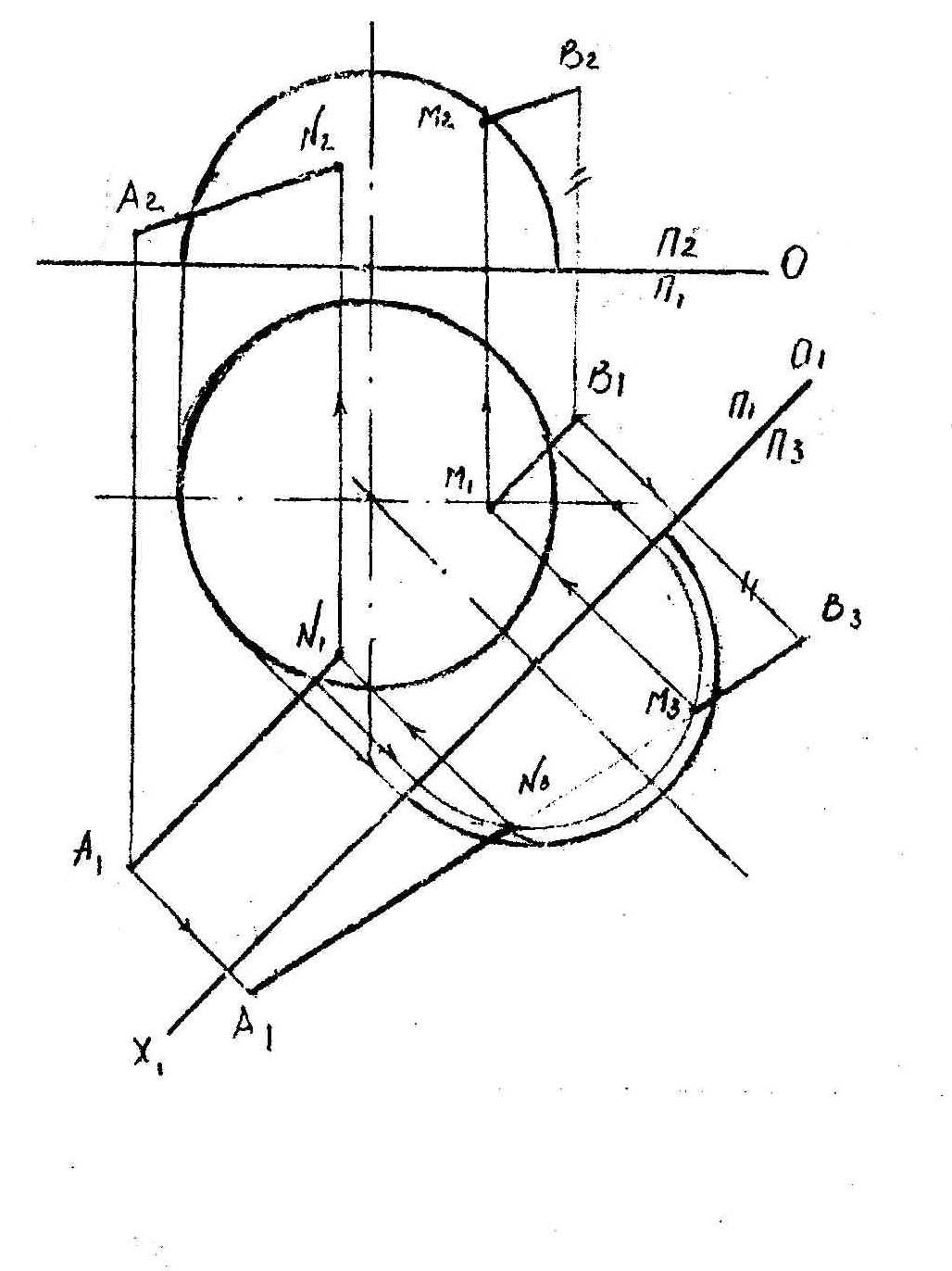
Решение задачи с шаром ясно из чертежа. Плоскости N и Т позволяют легко найти точки 7-К и 5-5, определяющие оси эллипса, в который проецируется «наклонная» окружность от секущей плоскости N.
Решение задачи с пирамидой легко понять из чертежа.
В нижеследующих примерах представлены тела с вырезами, линии, пересечения которых представляют собой кривые второго порядка. Контрольные точки этих сечений (А, В, С, К) хотя и лежат за пределами выреза, хорошо помогают выявлению характера кривых.
Лекции 15, 16. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Слово аксонометрия в переводе с греческого – измерение по осям. Сущность метода параллельного аксонометрического проецирования заключается в том, что предмет относят к системе координат и затем проецируют параллельными лучами на плоскость вместе с координатной системой.
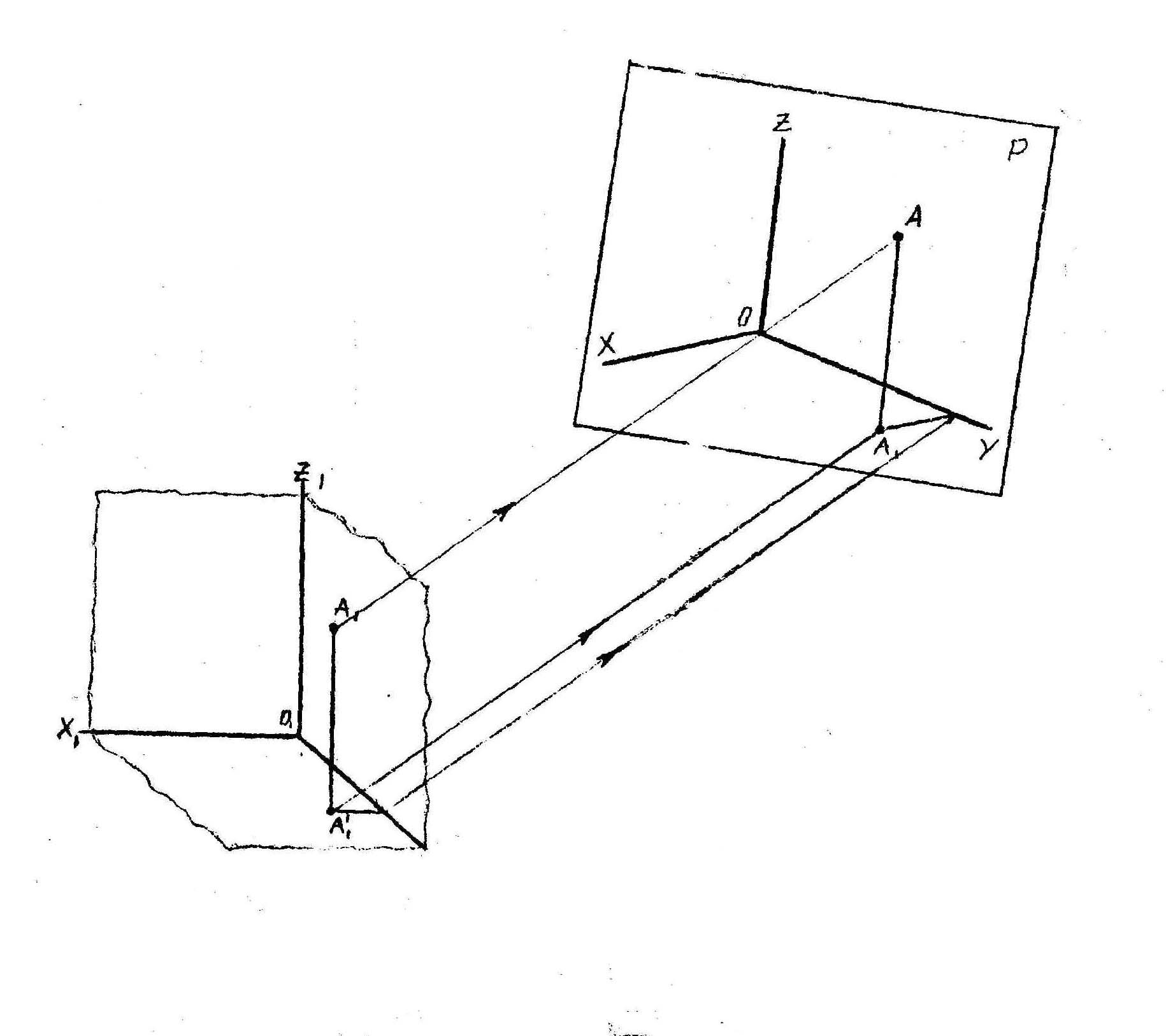
Р – аксонометрическая (картинная) плоскость проекций. Аксонометрическая проекция А и ее вторичная проекция А1определяют положение точки в пространстве.
Искажение отрезков осей координат при их проецировании на плоскость Р характеризуется показателями искажения. Показателем искажения называется отношение длины проекций отрезка оси на картине к его истинной длине.
Показатели искажения по отдельным осям:
I = OX ; I = OY I = OZ
По оси ОХ S O1X1 по оси ОYtO1Y1 по оси OZ U O1Z1
В зависимости от соотношения показателей искажения аксонометрические проекции могут быть:
1. Изометрическими – если показатели
искажения по всем трем осям равны между
собой ![]()
2. Диметрическими – по двум осям равны,
а третий отличается от первых двух
![]()
3. Триметрическими – все три показателя различны.
![]()
![]()
Аксонометрические проекции отличаются по тому углу , который образует проецирующий луч с плоскостью проекций Р:
при = 900– прямоугольная аксонометрия;
при 900– косоугольная аксонометрия.
Из бесчисленного множества аксонометрических изображений ГОСТ рекомендует следующие:
Прямоугольная изометрия
Углы между осями 1200и коэффициент
искажения![]() ,т.е. все размеры при проецировании
сокращены в 0,82 раза.
,т.е. все размеры при проецировании
сокращены в 0,82 раза.
ГОСТ рекомендует к применению увеличенную аксонометрию.
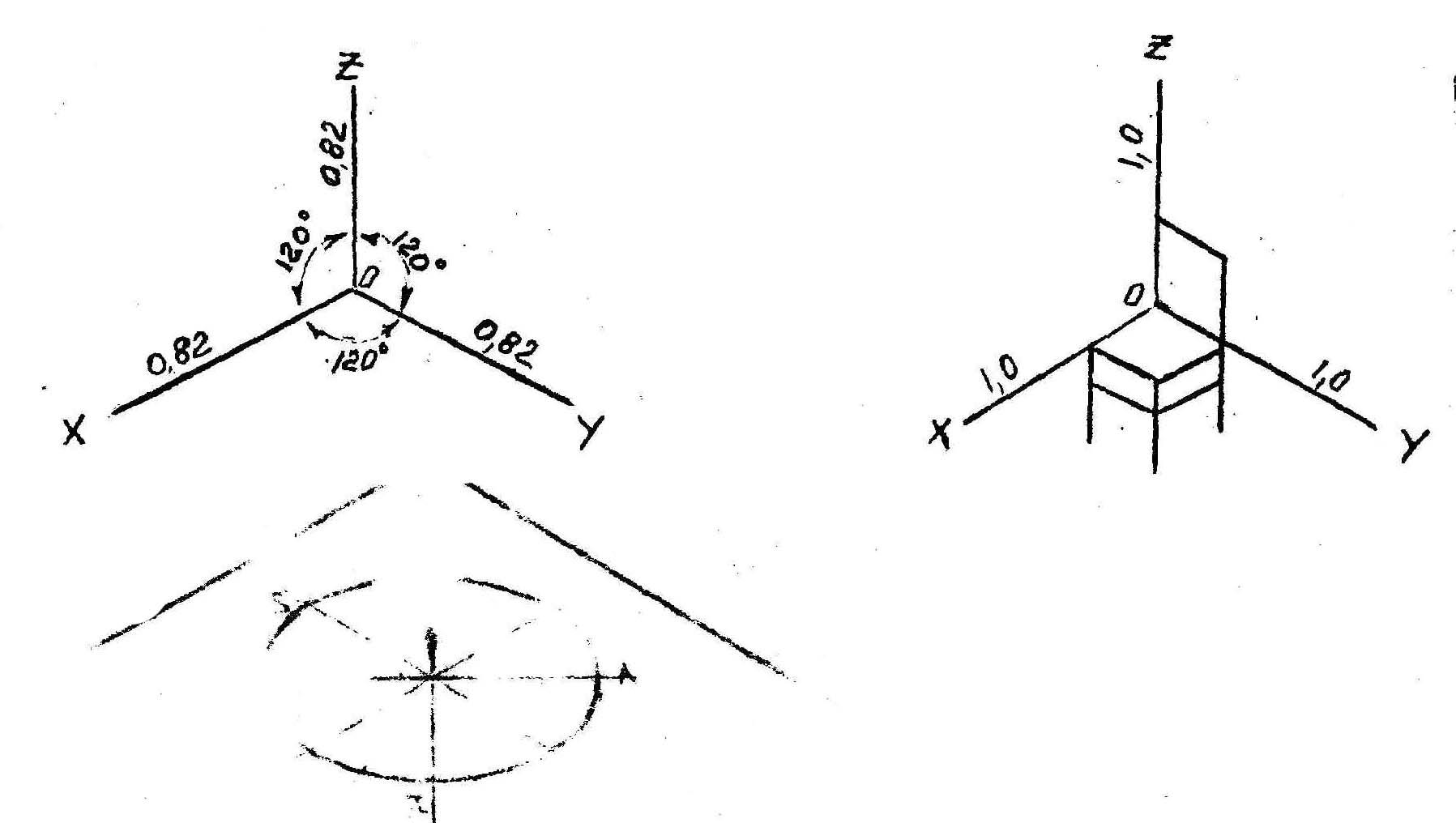
Теоретическая Практическая
(нормальная) ( увеличенная)
Прямоугольная диметрия
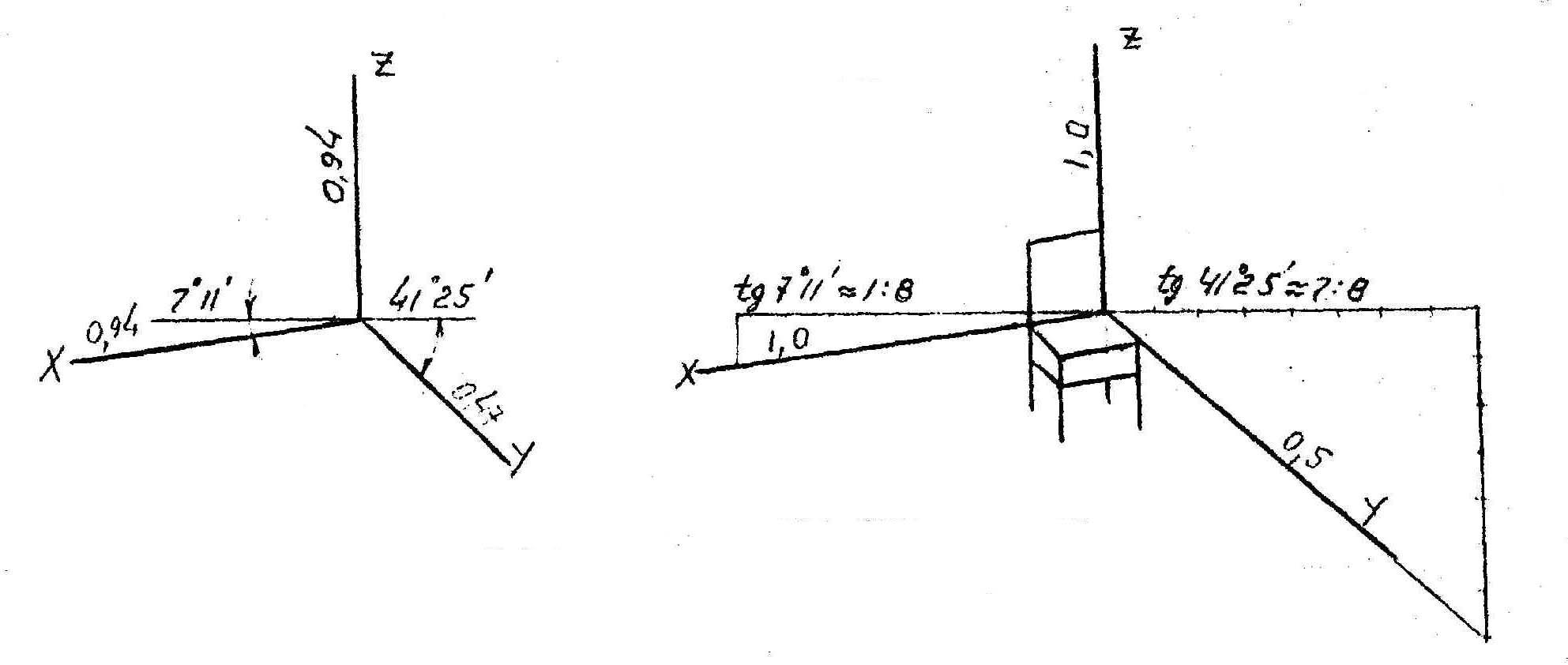
Теоретическая Практическая
(нормальная) (увеличенная)
Косоугольная (фронтальная) диметрия
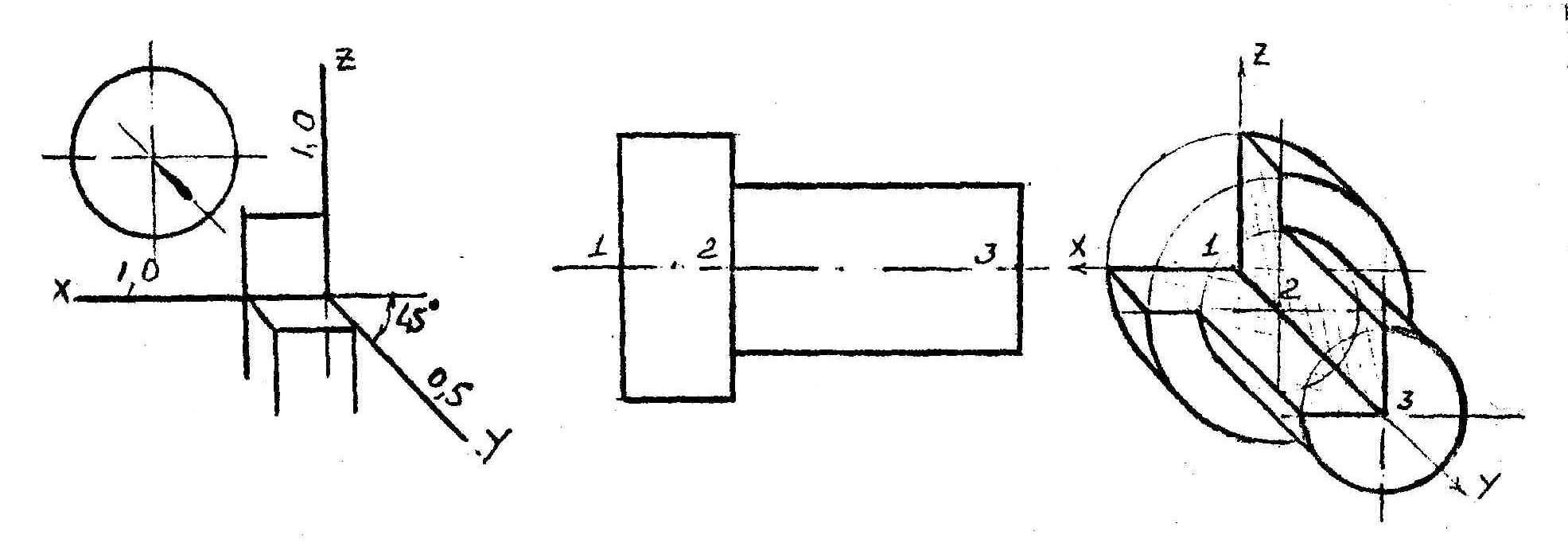
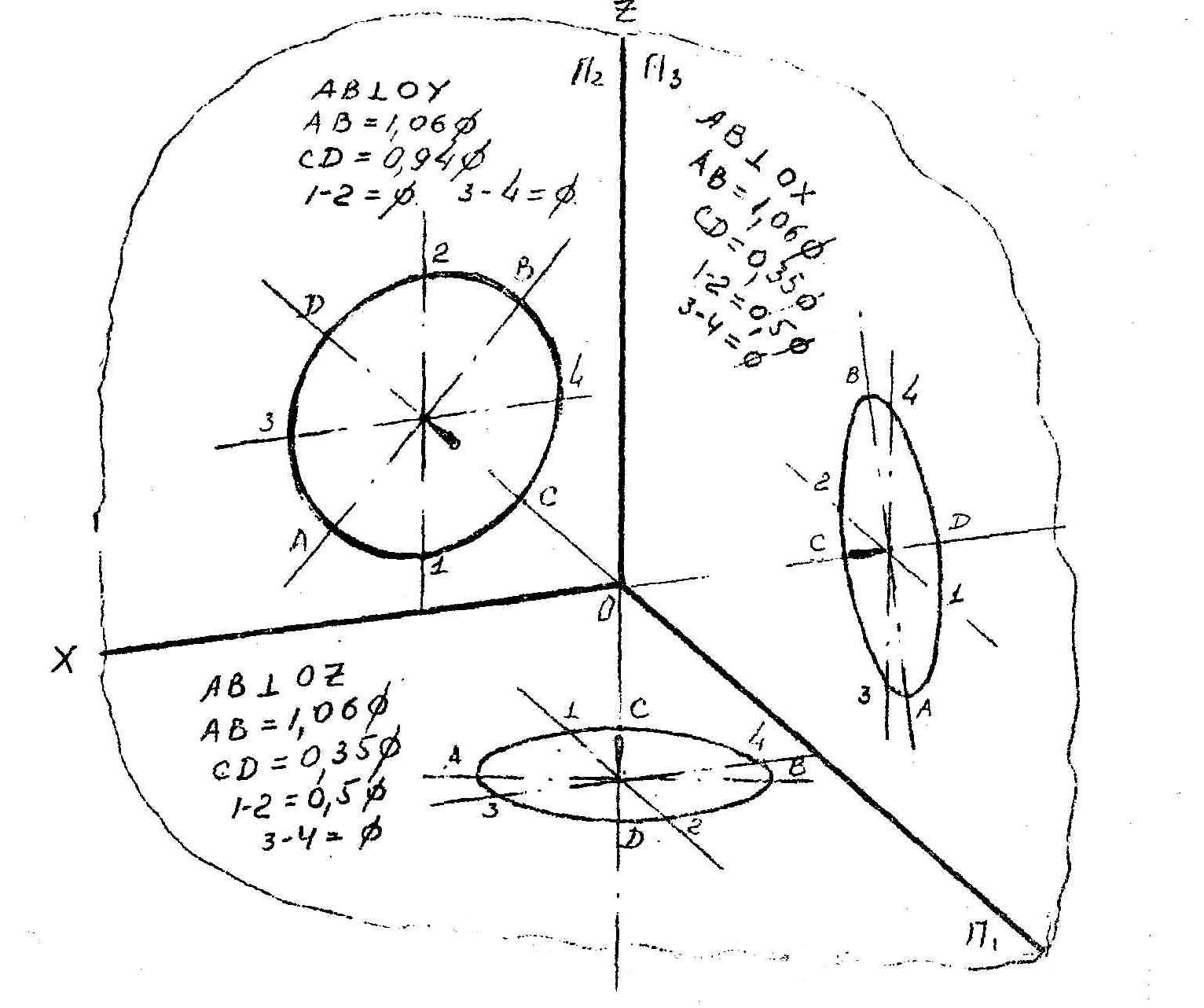
Окружность в прямоугольной изометрии
На чертеже в увеличенной изометрии представлена окружность 30 мм, плоскости которой параллельны соответствующим плоскостям проекций П1, П2, П3.
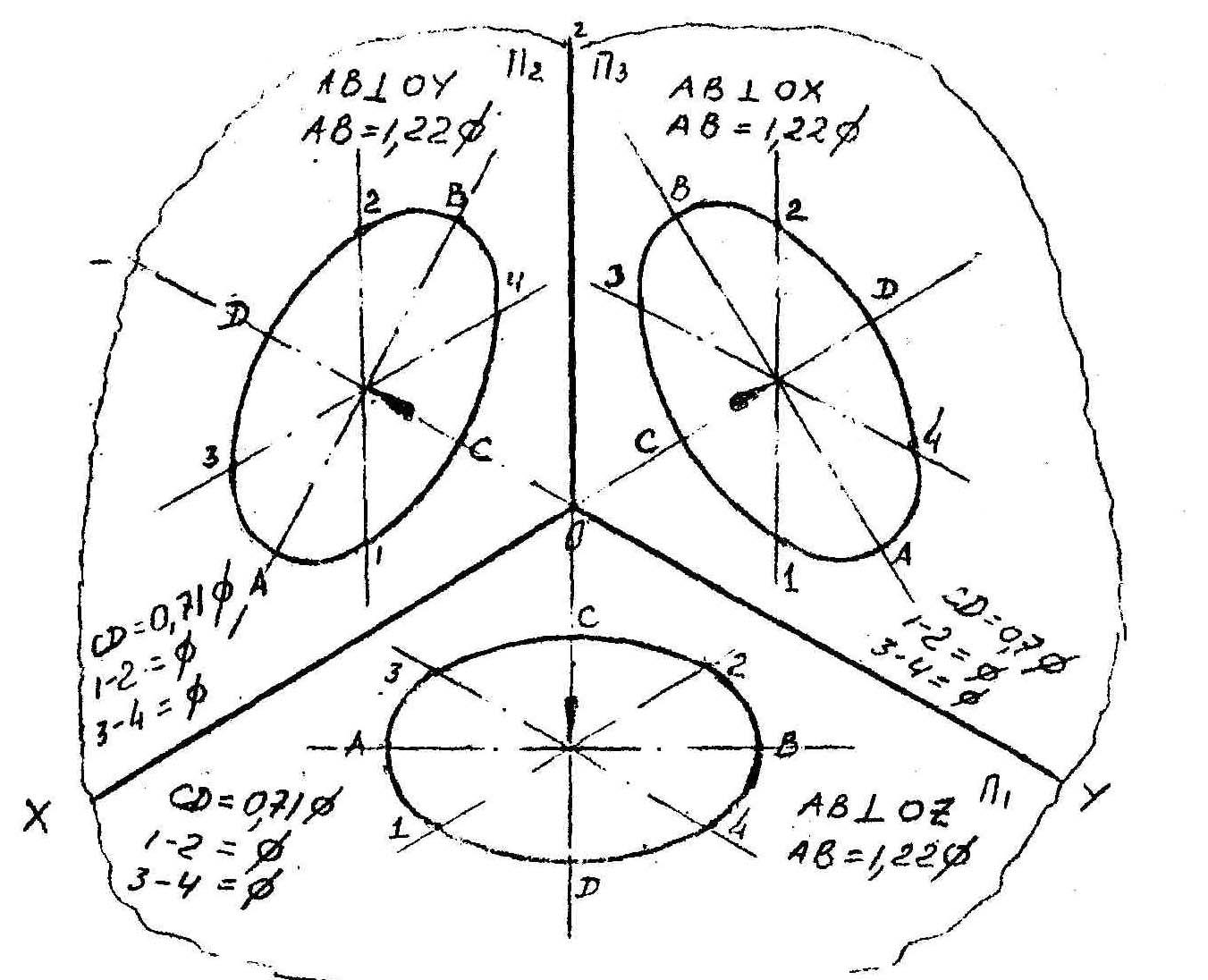
Окружность в прямоугольной диметрии
На чертеже в увеличенной диметрии представлена окружность 30 мм, плоскости которой параллельны соответствующим плоскостям проекции П1, П2, П3.
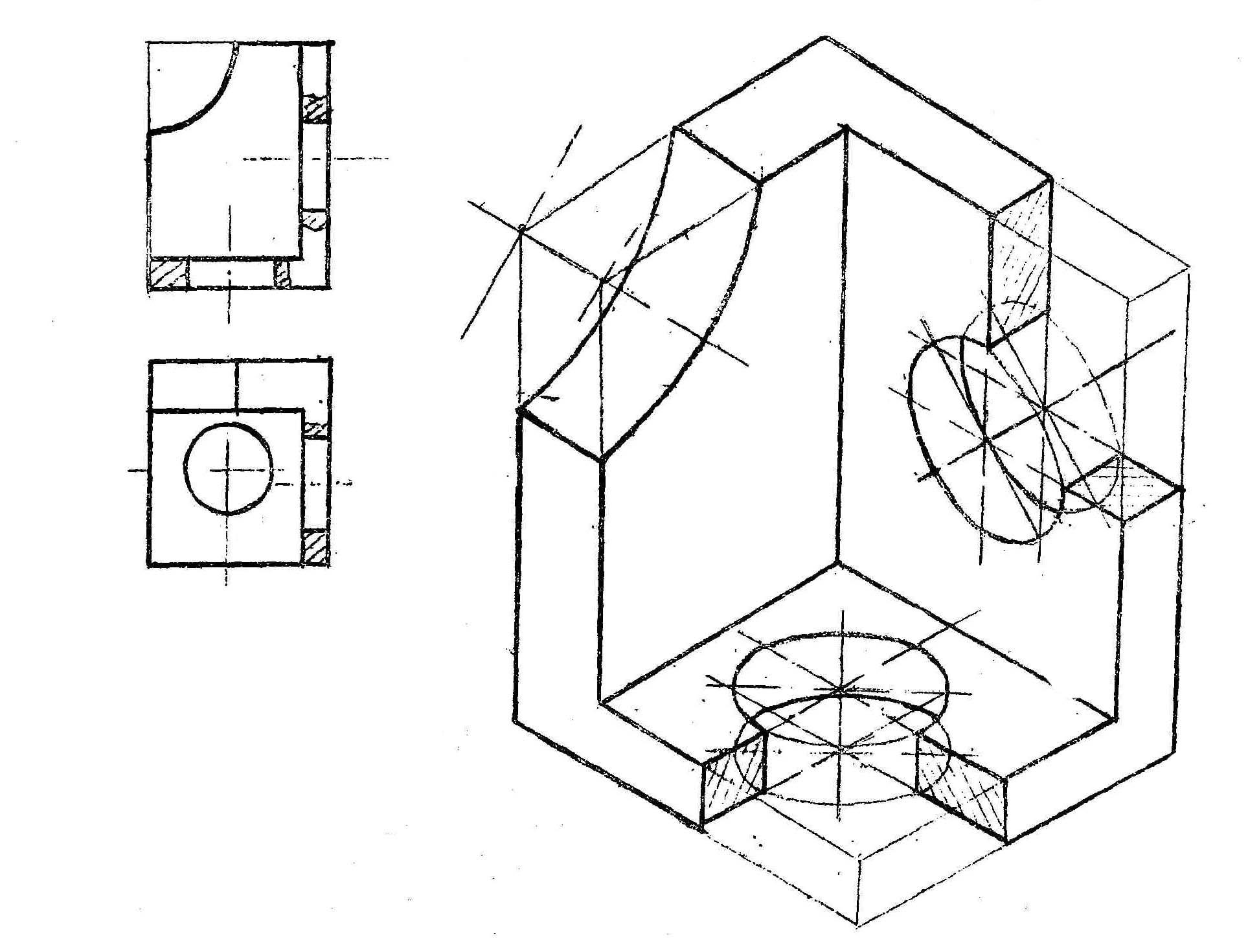
Для примера представлена фигура в практической изометрии с вырезами для усиления объемности изображения.
Учебное издание