10, 11, 12 вопрос

7

Вопрос 10

Химический потенциал

1)Для закрытых систем, в которых совершается только механическая работа, свободная энергия системы (энергия Гиббса G и энергия Гельмгольца F) зависит только от внешних условий. Если в системе протекают химические реакции или происходит обмен с окружающей средой веществом, сопровождающиеся изменением состава системы, то G и F будут зависеть и от состава системы:

G = f(p, T, n₁, n₂, …, n_k),

F = f(V, T, n₁, n₂, …, n_k),

где n₁, n₂, …, n_k – число моль 1-го, 2-го, …, k-го компонентов.

При р, Т = const изменение энергии Гиббса (полезная работа) системы обусловлено только изменением состава системы:

(1)

Введем обозначение:

,

где μ_i – химический потенциал i-го компонента.

Аналогично,

.

Таким образом, химический потенциал характеризует изменение свободной энергии системы (G или F) при изменении количества i-го компонента на бесконечно малую величину при постоянстве соответствующих внешних параметрах и количествах всех остальных компонентов.

Свободная энергия – это общее свойство системы, химический потенциал характеризует свойства отдельного компонента, входящего в систему.

При р, Т = const уравнение (1) запишется:

,

. (2)

Это уравнение выражает связь между общим свойством системы и свойствами каждого ее компонента. Проинтегрируем уравнение, приняв _i = const:

.

Для индивидуального вещества

G = n или , Дж/моль,

т.е. химический потенциал индивидуального вещества – это мольная энергия Гиббса.

При равновесии dG = 0, следовательно,

. (3)

Уравнение (3) – общее условие равновесия в системе с переменным составом при р, Т = const.

2) Выражения для химического потенциала компонента

Система	Уравнение	Примечание
Индивидуальный идеальный газ		0 – стандартный химический потенциал (при р = 1 атм), 0 = f(T); R – универсальная газовая постоянная, R = 8,31 Дж/(мольК); Т – температура, К; p – давление газа
Смесь идеальных газов		рi – парциальное давление газа, рi = xip; xi – мольная доля компонента; p – общее давление газовой смеси, p = рi; ;
	,
Идеальный жидкий раствор		xi – мольная доля компонента в растворе – стандартный хим. потенциал компонента (при xi0),
Смесь реальных газов		fi – парциальная фугитивность, или летучесть – фиктивное давление, подбираемое таким образом, чтобы сохранялась форма термодинамических уравнений (fiV = niRT);
Реальный жидкий раствор		ai – активность компонента, связана с концентрацией через коэффициент активности : В бесконечно разбавленных растворах γ → 1, аi → ci (хi или mi). – химический потенциал компонента реального жидкого раствора в стандартном состоянии.

Существует два основных способа выбора стандартного состояния компонента реального жидкого раствора – симметричный и несимметричный.

Симметричный способ. Выбирается одинаковое стандартное состояние для растворителя и растворенного вещества – состояние чистого компонента при температуре раствора. Способ чаще применяется для растворов неэлектролитов.

Несимметричный способ. Выбирается различное стандартное состояние для растворителя и растворенного вещества. Для растворителя – как и в симметричном способе. Для растворенного вещества за стандартное выбирается состояние вещества в бесконечно разбавленном растворе. Способ наиболее часто используется в термодинамике растворов электролитов.

Вопрос 11

химическое равновесие

1)Протекание самопроизвольного процесса в термодинамической системе сопровождается уменьшением свободной энергии системы (dG < 0, dF < 0). При достижении системой минимума свободной энергии устанавливается химическое равновесие, при котором dG = 0 и dF = 0.

Химическое равновесие является динамическим, т.е. соответствует одновременному протеканию процесса в противоположных направлениях с одинаковой скоростью.

Химическое равновесие подвижно – любое бесконечно малое внешнее воздействие на равновесную систему вызывает бесконечно малое изменение ее состояния.

2) Уравнение изотермы химической реакции

Рассмотрим условную реакцию, протекающую в идеальной газовой фазе при p, T = const:

аА + bВ = eЕ + lL.

Пусть в реакцию вступило бесконечно малое количество вещества А (dn_A моль); с ним прореагировало dn_B моль вещества В и образовалось dn_E моль вещества E и dn_L моль L. Изменения количества исходных веществ и продуктов реакции составили: –dn_A, – dn_B (количество исходных веществ уменьшается, поэтому знак «–»), dn_E и dn_L.

В результате этого самопроизвольного процесса изобарный потенциал системы G изменился на величину

,

. (1)

Выразим dn_A, dn_B, dn_E, и dn_L через коэффициенты уравнения реакции. Согласно уравнению:

с а моль вещества А реагирует b моль вещества В

с dn_A моль dn_B,

тогда

.

Аналогично,

; .

Подставим в (1):

.

Умножим левую и правую часть уравнения на а и разделим на dn_A:

.

Так как химический потенциал равен мольной энергии Гиббса , то

. (2)

Применим выражение для химического потенциала компонента идеальной газовой смеси:

.

Химический потенциал вещества А равен

,

и т.д. для других компонентов.

Подставим в (2):

,

, (3)

где – изменение энергии Гиббса в стандартных условиях

Уравнение (3) – уравнение изотермы химической реакции.

При равновесии ΔG = 0, парциальные давления компонентов становятся равновесными и из уравнения изотермы (3) следует, что

. (4)

Так как правая часть уравнения (4) зависит только от температуры и природы реагентов, то и левая часть есть постоянная величина при Т = const.

Введем обозначение:

, (5)

где К_р – термодинамическая константа равновесия. Нижний индекс «р» означает, что константа равновесия выражена через парциальные давления компонентов.

Уравнение (5) выражает известный закон действия масс: отношение произведения равновесных парциальных давлений продуктов реакции, взятых в степенях, равных стехиометрическим коэффициентам к аналогичному произведению для исходных веществ при данной температуре есть величина постоянная.

Тогда

.

Подставим в (3):

. (6)

Если известна константа равновесия реакции и парциальные давления (или концентрации) реагентов с помощью уравнения (6) можно оценить знак G и сделать вывод о направлении самопроизвольного процесса: реакция будет протекать самопроизвольно, если

,

т.к. при этом G < 0.

В зависимости от вида системы, в которой протекает реакция (идеальная, реальная) константу равновесия выражают через парциальные давления K_p, концентрации K_c, мольные доли K_x, активности K_a, фугитивности K_f:

, и т.п.

Парциальное давление газа p_i связано с его мольной долей x_i и молярной концентрацией c_i соотношением

,

где p – общее давление реакционной смеси, p = p_i.

Тогда

,

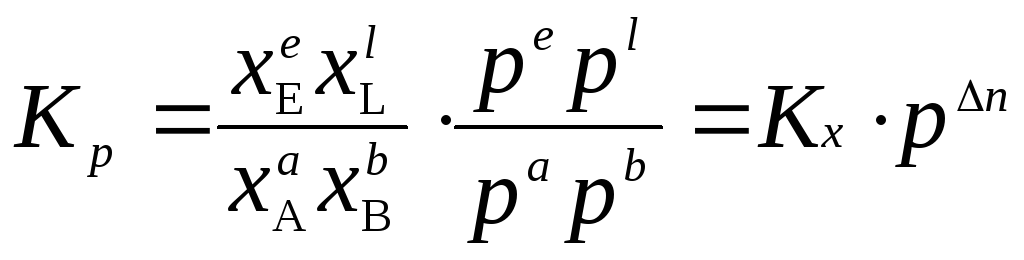где n = e + l – (a + b) – разность между стехиометрическими коэффициентами газообразных продуктов реакции и исходных веществ.

Аналогично,

.

Таким образом,

.

Если n = 0, то

.

K_p, K_c = f(T), а K_x = f(T, p).

Если химическая реакция протекает с участием конденсированных веществ (твердых или жидких), то закон действия масс записывается только для газообразных участников реакции. Например, для реакции

СаСО_3(тв) = СаО_(тв) + СО_2(г)

.

Вопрос 12

Влияние условий проведения реакции

на смещение химического равновесия

При постоянстве внешних условий система может находиться в состоянии равновесия сколь угодно долго. Если оказать на систему какое-либо внешнее воздействие, равновесие нарушается; в системе возникает самопроизвольный процесс, продолжающийся до установления равновесия уже при новых условиях.

- Влияние концентрации реагирующих веществ.

Если в равновесную реакционную смесь добавить исходное вещество, начнется самопроизвольный процесс, направленный в сторону его расходования и образования продуктов реакции. Такой же процесс будет протекать, если уменьшить концентрацию продуктов реакции, например, удалять их из реактора.

- Влияние давления (для реакций, идущих в газовой фазе).

Давление влияет на положение равновесия только для реакций, протекающих с участием газообразных веществ. Направление смещения равновесия будет определяться знаком Δn:

– если реакция идет с увеличением объема, т.е. Δn > 0, повышение давления сместит равновесие в сторону исходных веществ, выход продуктов сократится;

– для реакций, протекающих с уменьшением объема (Δn < 0), повышение давления будет способствовать увеличению выхода продуктов реакции.

Влияние давления на равновесные системы, в составе которых нет газов, пренебрежимо мало.

- Влияние температуры на химическое равновесие

Воспользуемся уравнениями:

,

.

Совместным решением этих уравнений получим:

,

.

Полученное выражение продифференцируем по температуре:

(7)

Уравнение (7) – уравнение изобары Вант-Гоффа – характеризует влияние температуры на константу химического равновесия.

Анализ уравнения.

Для экзотермических реакций Н < 0, следовательно,

.

Это означает, что с повышением температуры константа равновесия экзотермической реакции уменьшается и равновесие смещается в сторону образования исходных веществ. Выход продуктов реакции сокращается.

Для эндотермических реакций H > 0, следовательно,

.

Это означает, что с повышением температуры константа равновесия эндотермической реакции возрастает и равновесие смещается в сторону увеличения выхода продуктов реакции.

Действие рассмотренных факторов обобщает принцип смещения равновесия, называемый также принципом Ле Шателье – Брауна:

Если на систему, находящуюся в состоянии истинного равновесия, оказывается внешнее воздействие, то в системе возникает самопроизвольный процесс, компенсирующий данное воздействие.