Теоретическая механика

Теоретическая механика – есть наука об общих законах механического движения и взаимодействия материальных тел.

Теоретическая механика является базой для всех технических дисциплин.

По характеру рассматриваемых задач она подразделяется на статику, кинематику и динамику.

1. Статика

Статикой называется раздел теоретической механики, в котором излагается общее учение о силах, и изучаются условия равновесия тел, находящихся под действием сил.

Основные определения

Абсолютно твердое тело – это такое тело, расстояние между двумя любыми точками которого всегда остается постоянным.

Сила – есть количественная мера механического взаимодействия тел.

Сила – величина векторная, она определяется тремя параметрами: линией действия, направлением вдоль линии и величиной (модулем). Сила – это скользящий вектор, который можно перемещать вдоль линии действия.

Прямая, вдоль которой направлена сила, называетсялинией действия силы.

Вся совокупность сил, действующих на твердое тело, называется системой сил.

Равнодействующая сила – это такая сила, которая заменяет действие системы сил на твердое тело (сила эквивалентна системе).

Уравновешенной называется система сил, под действием которой тело находится в состоянии равновесия.

Под состоянием равновесия в механике понимают состояние покоя или равномерного и прямолинейного движения.

Сила равная по модулю равнодействующей, противоположно ей направленная вдоль той же линии действия называется уравновешивающей силой.

Аксиомы статики

Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без доказательств и называемых аксиомами или принципами статики.

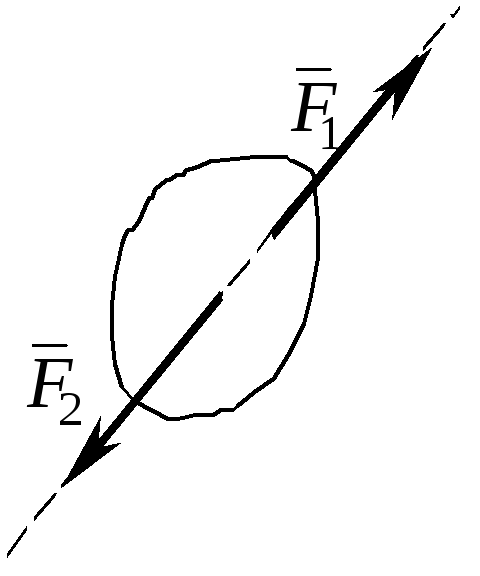
Аксиома 1. Если тело находится в равновесии под действием двух сил, то эти силы имеют общую линию действия, противоположны по направлению и равны по величине.

, (1.1)

Аксиома 2. Действие системы сил на тело не изменится, если к этой системе добавить или от нее отнять уравновешенную систему сил.

,

(1.2)

Следствие (из аксиом1 и 2): Действие силы на абсолютно твердое тело не изменится, если силу перенести в любую точку тела по линии действия.

Пусть есть сила F в точке A. В точку B на линии действия силы F помещаем уравновешенную систему сил F₁ и F₂, так чтобы . Но тогда- также уравновешенная система, ее можно убрать. В итоге остаетсяв точкеB.

Аксиома 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах как на сторонах.

,

. (1.3)

Пользуясь аксиомой 3 можно не только складывать любое количество сил, но и раскладывать на любое число направлений.

Аксиома 4. Всякому действию одного тела на другое существует равное по величине, но противоположное по направлению противодействие.

Силы, возникающие при взаимодействии, не образуют уравновешенную систему, так как приложены к разным телам.

Аксиома 5. Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать мгновенно отвердевшим (абсолютно твердым).

Аналитическое задание и сложение сил

Силы можно задавать и складывать аналитически с помощью их проекций на оси координат.

Проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца вектора силы.

,.

Проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.

Пусть сила F задана через свои проекции на координатные оси F_x, F_y, F_z. По приведенному выше определению проекции определяются выражениями

(1.4)

Углы в (1.4) удовлетворяют уравнению

. (1.5)

Возводя в квадрат (1.4) и складывая, с учетом (1.5) получим модуль силы

(1.6)

и направляющие косинусы

. (1.7)

Направляющие косинусы указывают положение вектора силы в пространстве по отношению к координатным осям.

Зная проекции сил на координатные оси, их можно складывать аналитически.

Проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось

. (1.8)

Модуль равнодействующей и направляющие косинусы определяются по (1.6) и (1.7)

, (1.9)

. (1.10)