1.2. Модификации формулы включения и исключения

2.а. Формулу (2.1) можно обобщить для определения числа элементов, обладающих в точности k свойствами (0  k  n):

N(k) = + …+ (– 1)^s–k+ …

+ (–1)^n–k N(1, 2, … , n). (3.4)

Пример 3.2. В отделе НИИ каждый сотрудник владеет хотя бы одним иностранным языком. Известно, что английским языком владеют 6 человек, немецким – 6, французским – 7, английским и немецким – 4, немецким и французским – 3, английским и французским – 2, все три языка знает 1 человек. Определить, сколько всего человек в отделе, сколько человек владеют только английским, только немецким, только французским, и сколько человек знает только 1 иностранный язык.

Решение. Согласно условиям задачи N(0) = 0, т.к. в отделе нет сотрудников, не владеющих иностранными языками. Следовательно, по формуле (3.1) получаем:

N = – + N(1, 2, 3) (3.5)

N = 6 + 6 + 7 – 4 – 3 – 2 + 1 = 11 человек всего в отделе.

Для вычисления остальных показателей также воспользуемся формулой (3.5). Найдем, например N(только А) – число человек, не владеющих никаким другим языком, кроме английского. Для этого формулу (3.5) надо применить только к множеству людей, владеющих английским языком. В этом случае n = 2. Тогда N = N(A), N(1) и N(2) – число людей, владеющих помимо английского еще немецким и французским, соответственно, N(1, 2) – число людей, владеющих помимо английского еще одновременно немецким и французским. Отсюда

N(только A) = N(A) – N(А и Н) – N(А и Ф) + N(А и Н и Ф) =

6 – 4 – 2 + 1 = 1.

Аналогично

N(только Н) = N(Н) – N(А и Н) – N(Н и Ф) + N(А и Н и Ф) =

6 – 4 – 3 + 1 = 0.

N(только Ф) = N(Ф) – N(Ф и А) – N(Ф и Н) + N(А и Н и Ф) =

7 –2 – 3 + 1 = 3.

Вычислим теперь N(1) – число людей, владеющих только 1 языком. Воспользуемся формулой (3.4) при k = 1.

N(1) = N(А) + N(Н) + N(Ф) + (–1)^2–1 [N(А и Н) + N(Н и Ф) + N(А и Ф)] + (–1)^3–1 N(А и Н и Ф) = 6 + 6 + 7 – 2(4 + 3 + 2) + 31 = 4.

Такой же результат получим, если сложим N(только A) + N(только Н) + N(только Ф).

2.б. Формулу (3.1) можно также интерпретировать, как подсчет мощностей пересечений различных множеств, т.е. дать теоретико-множественное представление принципа включения и исключения. Пусть имеем некоторое конечное множество А и его подмножества А_j, j = 1,…, n. Тогда теоретико-множественный аналог формулы (3.1) будет иметь вид:

= |A| – + + …

+ (– 1)^k+ …+ (–1)ⁿ .

2. Формулы обращения

2.1. Теорема обращения. Пусть имеем два семейства комбинаторных чисел {a_n,k} и {b_n,k}, зависящих от целочисленных параметров n, k, причем 0  k  n.

Теорема 3.1. Пусть для любых n и k, 0  k  n справедливы зависимости и пусть существуют такие числа_n,k,i, что для любых k  n и m  n выполняются равенства

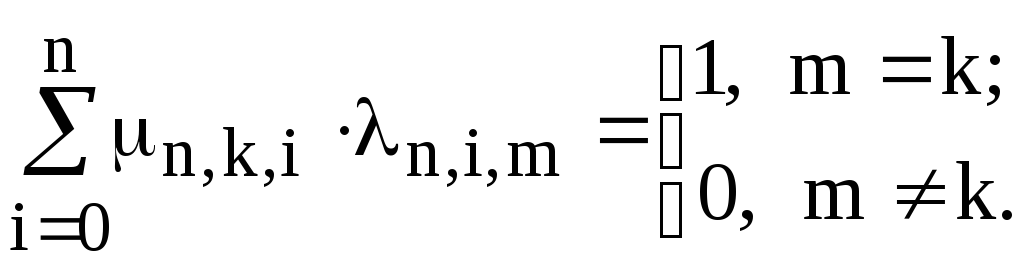
Тогда для всех k  n имеет место формула обращения:

.

Доказательство.

= ==b_n,k,

что и требовалось доказать.

2.2. Примеры использования формулы обращения. Зависимость между числами _n,k,i и _n,k,i, фигурирующая в условиях теоремы 3.1, по сути означает, что эти числа образуют систему взаимно обратных матриц, т.е. смысл теоремы весьма прост, если не сказать – тривиален. Для произвольных чисел a_n,k и b_n,k она не дает никакой ценной информации, поскольку найти требуемые числа _n,k,i в общем случае столь же трудно, как и решить исходную систему уравнений относительно b_n,k. Однако, для многих специальных случаев, в частности, комбинаторных чисел, удается найти _n,k,i в явном виде. В этом особенность данной формулы. Рассмотрим ее применение для обращения биномиальных коэффициентов.

Лемма 3.1.

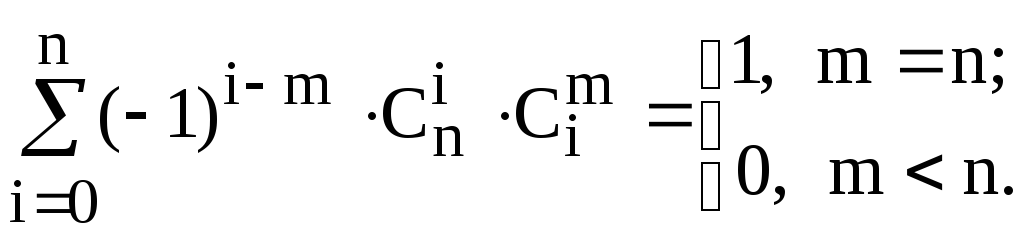
Доказательство. Имеем:

= =

= =.

Следовательно,

= = В.

Так как при k < 0 и при k > n , то в полученном выражении можно суммировать не отi = 0, i = m. То есть

В = =.

Но при m < n имеем:

= = 0.

Последнее равенство следует из свойства 5 чисел сочетания.

А при m = n имеем:

= = 1,

что и требовалось доказать.

Теорема 3.2. Если , то.

Доказательство. Здесь и. Приk  n, m  n имеем:

= ===

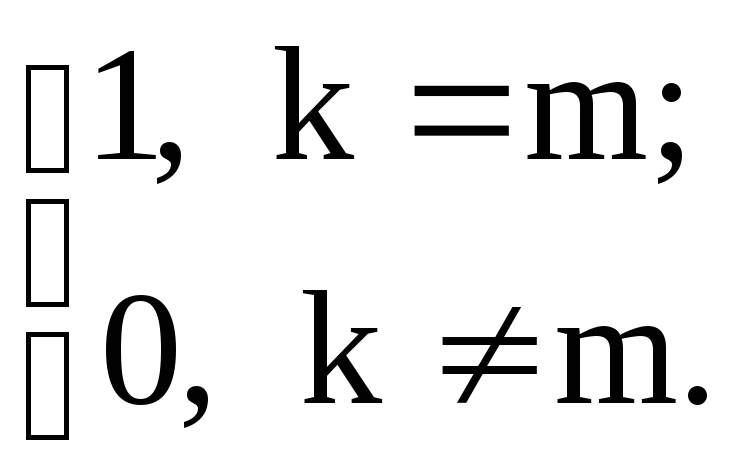
Это означает, что выполнены условия теоремы 3.1, а, следовательно, теорема доказана.

Теорема 3.3. Если , то.

Доказательство аналогично.