2.6. Свойства чисел сочетаний

1. =. Это свойство вытекает из формулы числа сочетаний.

2. =+.

Доказательство. Разобьем все r-сочетания на два класса. К первому классу отнесем сочетания, содержащие объект a_n, ко второму классу – не содержащие a_n. Так как в первом классе меняются только r – 1 элементов из n – 1 возможных, то он содержит r – 1-сочетания из n – 1-множества, следовательно, в нем элементов. Второй класс содержит всеr-сочетания из n – 1-множества, т.к. в них нет одного элемента – a_n. Следовательно, в нем элементов. Общее число сочетаний, согласно правилу суммы равно+, что и требовалось доказать.

Данное свойство позволяет легко построить рекуррентный процесс вычисления всех чисел сочетаний. Положим по определению для любого n  0 (ноль элементов из любого множества, в том числе – пустого, можно выбрать 1 способом, кроме того, по определению 0! = 1 – см. формулу из 2.4) и(отрицательное количество элементов выбрать невозможно). Организуем двойной цикл для вычисления всех,r  m  n:

for m := 1 to n do

for r := 0 to m do := +

Описанный процесс удобно представить в виде таблицы, называемой треугольником Паскаля:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…………………….

В таблице каждая m-я строка состоит из чисел ,r = 0, … m, каждый элемент равен сумме двух элементов, расположенных над ним (пустое место считается нулем).

3.

Доказательство. Пусть имеем последовательность из n двоичных разрядов, содержащих 0 или 1. Очевидно, что каждую такую последовательность можно рассматривать, как n-размещение с повторениями из элементов 2-х типов, значит, количество этих размещений равно 2ⁿ.

Теперь рассмотрим некоторое множество из n объектов – а₁, … а_n, из которого будем образовывать все возможные сочетания без повторений, включая: 0-сочетания (не выбирается ни один объект), 1-сочетания и т.д., n-сочетания. При этом любую из упомянутых выше последовательностей из 0 и 1 можно интерпретировать, как перечень элементов, отбираемых в сочетание – если на k-м месте последовательности стоит 1 – элемент а_k отобран, если 0 – не отобран. Очевидно, что таким образом будут перечислены все бинарные n-последова-тельности. По правилу суммы общее число таких сочетаний, а, значит – и бинарных последовательностей равно Свойство доказано.

Замечание. Каждая отбираемая в сочетание группа элементов представляет собой некоторое подмножество исходного множества из n объектов. Следовательно, число всех подмножеств (включая пустое) множества из n элементов равно 2ⁿ.

3. Комбинаторные конфигурации в алгебре и анализе

Многие важные формулы алгебры и математического анализа (и других разделов математики) имеют наглядную комбинаторную интерпретацию или доказываются с использованием правил комбинаторики.

3.1. Бином Ньютона. – формулабинома Ньютона. В частности, (х + у)² = х² + 2ху + у²; (х + у)³ = х³ + 3х²у + 3ху² + у³ и т.д.

Доказательство. Раскроем скобки выражения (х + у) ⁿ = (x + y)(x + y)…(x + y). В результате получим сумму членов вида . Например (х + у) ³ = ххх + хху + хух + хуу + ухх + уху + уух + ууу. Приведем подобные члены, подсчитав число таких произведений при каждом k = 0,…, n. Каждое такое выражение – не что иное, как перестановка повторениями из 2-х элементов. Полагая n₁ = k, n₂ = n – k, получим, что число этих перестановок равно Р(k, n – k) = (см. пп. 2.3, 2.4), т.е. множитель при х^kу^{n – k} совпадает с ,что и требовалось доказать.

С помощью формулы бинома легко получить новые свойства чисел сочетаний.

5. . Доказать легко с использованием бинома Ньютона на основе тождества (1 – 1)ⁿ = 0.

6. .

Доказательство. Имеем: n2^n–1 = n(1 + 1)^{n –1} = . В свою очередь при любом р выполняется равенство:

= =.

Следовательно, . Переобозначим индекс суммирования, положивp + 1 = k. Имеем:

,

что и требовалось доказать. В последнем равенстве формально введено равное нулю слагаемое при k = 0.

3.2. Полиномиальная формула. Формулу бинома можно обобщить на случай нескольких слагаемых: (х₁ + х₂ + … + х_k)ⁿ.

Запишем эту формулу в виде произведения одинаковых сомножителей и перемножим. Получим все возможные n-размещения с повторениями из объектов х₁, х₂ , … , х_k. Приведем подобные, сосчитав число повторений каждого слагаемого вида . Для этого надо определить число слагаемых, в которых символ х₁ повторяется n₁ раз, х₂ – n₂ раз, и т.д., х_k повторяется n_k раз. Каждое такое слагаемое – это перестановка с повторением n_j раз элемента х_j, j = 1,…k. Число таких перестановок равно Р(n₁, n₂ ,…, n_k),  n_j = n. Следовательно

(х₁ + х₂ + … + х_k)ⁿ = .

Выражение n₁ + … + n_k = n в значке суммы означает, что перебираются все (целые неотрицательные) значения n₁,…, n_k, удовлетворяющие данному условию.

Например: (x + y + z)⁴ = P(4, 0, 0)x⁴ + P(0, 4, 0)y⁴ + P(0, 0, 4)z⁴ + P(3, 1, 0)x³y + P(3, 0, 1)x³z + P(2, 2, 0)x² y² + P(2, 1, 1)x² y z + P(2, 0, 2)x² z² + P(1, 3, 0)x y³ + P(1, 0, 3)x z³ + P(1, 1, 2)x y z² + P(1, 2, 1)x y² z + P(0, 3, 1)y³ z + P(0, 1, 3)y z³ + P(0, 2, 2)y² z².

Напоминаем, что здесь Р(a, b, c) = , например Р(2, 1, 1) == 12.

3.3. Ряд Ньютона. Формулу бинома можно обобщить на случай нецелой степени, в результате получим выражение:

(у + х)^ = у^ +  у^–1х + + … + ++…

При целом значении  формула содержит конечное число слагаемых, т.к. для k >  коэффициенты при у^–kх^k обращаются в ноль. При нецелом  получается бесконечный степенной ряд. Найдем радиус его сходимости. Представим бином в виде:

(у + х)^ = = у^ (1 + z)^ =

у^ .

Воспользуемся формулой Даламбера:

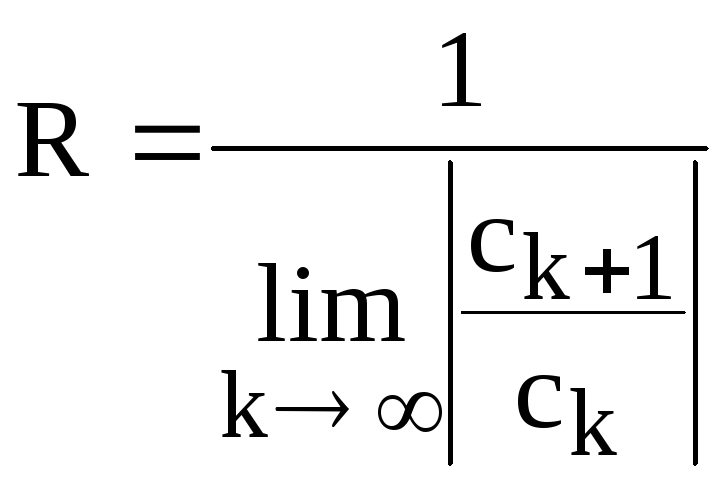, где .

Имеем: = –1 + – 1. Отсюда R = 1. Следовательно, ряд сходится при |z| < 1, т.е. при |x| < |y|. Если разложение в ряд происходит по степеням у, то ряд сходится при |у| < |х|.

Пример 1.8. = (1 – х)^–1 = 1 + ( – 1)( – х) +

+ = 1 + х + х² +…

– формула бесконечно убывающей геометрической прогрессии, которая сходится при |x| < 1.