Уравнение Гиббса – Гельмгольца

Рассмотрим изохорно-изотермическую систему (Т = const; V = const) и воспользуемся для характеристики этой системы функцией F = U – T·S. Так как , то, подставив это значение в уравнение функции свободной энергии, получим.

Рассмотрим изотермический переход системы из начального состояния в конечное, для которых ;.

Но

и ,

поэтому (1)

или .

Анализируя протекание процесса в изобарно-изотермических условиях (Т = const; р = const), путем аналогичных рассуждений придем к выводу, что(2)

или .

Уравнения (1) и (2) выражают величину максимальной работы через тепловой эффект реакции и называются уравнениями Гиббса-Гельмгольца.

Из уравнений видно, что теплота может служить мерой химического сродства только при Т = 00 К или при , т. е. при независимости величины работы от температуры.

8. Применение второго закона термодинамики к фазовым превращениям. Вывод дифференциальной формы уравнения Клаузиуса - Клапейрона для процесса кипения. Интегрирование уравнения Клаузиуса - Клапейрона и его анализ.

Применение второго закона термодинамики к фазовым превращениям.

Процессы перехода системы из одной фазы в другую называется фазовыми превращениями. К ним относятся процессы плавления, кристаллизации, испарения, кипения, конденсации, сублимации (возгонки) и полиморфные превращения.

Температура фазового превращения не зависит от количества равновесных фаз и является величиной постоянной (Т = const). Зависимость температуры фазового перехода от давления была установлена Клапейроном (1834 г.) и обоснована Клаузиусом (1850 г.).

Дифференциальная форма уравнения Клапейрона-Клаузиуса имеет вид:

,

где Н _ф.пр. - теплота (энтальпия) фазового превращения, Дж/моль; Т _ф.пр. - температура фазового превращения; V₁, V₂ - объёмы разных фаз.

Уравнения Клапейрона-Клаузиуса для частных случаев фазовых превращении:

1) Для процессов испарения и конденсации:

,

где Н_исп.- теплота испарения , Дж/моль; V_п - объём пара, л.; V_ж - объём жидкости, л. ; Т_кип - температура кипения, град.

2) Для процесса плавления и кристаллизации:

,

где Н_пл.- скрытая теплота плавления, Дж/моль; V_тв- объём твердого тела , л.; Т_пл.- температура плавления, град ;

3) Для процесса (сублимации) возгонки:

.

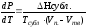где Н_субл. - теплота возгонки, Дж/моль; Т_субл. - температура сублимации, град.

4) Для процесса полиморфного превращения:

,

где Н_ - теплота полиморфного превращения, Дж/моль;

Т_ - температура полиморфного превращения, град.

Вывод дифференциальной формы уравнения Клаузиуса - Клапейрона для процесса кипения.

Рассмотрим процесс фазового превращения на примере кипенияжидкости.

Испарение - это фазовый переход на границе раздела жидкость пар или жидкости.

Кипение - это процесс, когда парообразование происходит не только с поверхности но внутри жидкости путём образования пузырьков пара жидкости и их выделения. При этом давление в пузырьках пара, находящихся в равновесии с жидкостью, равно давлению пара над жидкостью.

Температура кипения - это температура, при которой давление насыщенного пара жидкости равно внешнему давлению:

Р_{насыщ. пара} = Р_внеш.

Нормальнойназывается температура кипения жидкости, измеренная при нормальном давлении.

Уравнение Клапейрона-Клаузиуса (5.2.) можно преобразовать, приняв следующие приближения:

1. Поскольку V_п >> V_ж (например для воды мольный объем в парообразном состоянии при нормальных условиях равен V_п =22400 см³, а в жидком состоянии V_ж = 18 см³), то в уравнении можно пренебречь величинойи принять, что;

2. При невысоких давлениях и температурах (вдали от критических) можно применять уравнение состояния идеального газа (уравнение Клапейрона-Менделеева ) и к реальным системам. Тогда

,

где R - универсальная газовая постоянная.

Подставив уравнениев уравнение К-К, получим:

.

Это уравнение после преобразования:

принимает вид: .

Теплота испарения  зависит от температуры: c повышением температуры она понижается, а с понижением - повышается; при критической температуре теплота испарения равна нулю.

При температурах, далёких от критической, изменения теплоты испарения малы и поэтому в небольшом интервале температур, теплоту испарения можно считать величиной постоянной: =const.