Расчет изменения энтропии при различных термодинамических процессах и при протекании химических реакций.

1) Изохорический процесс V=const

->

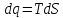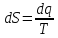
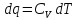
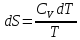
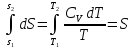
Получаем: ,

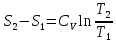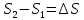
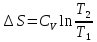
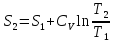
Если ν≠1 моль, то

,

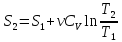
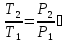
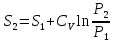
2) Изобарический процесс P=const

->

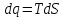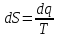
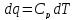
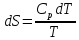
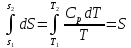
Получаем: ,

,

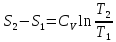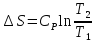
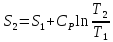для ν≠1 моль, то

,

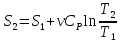
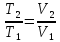
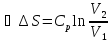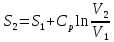
Все вышеприведенные уравнения справедливы для случая, что теплоемкость является величиной постоянной. Однако, известно, что C_p=f(t) и эта зависимость определяется интегральным рядом.

C_p=a+bT+cT²+c’T^-2

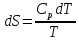
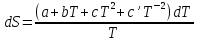
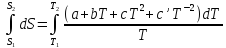
Интеграл суммы – сумма интегралов

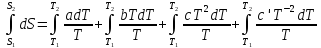
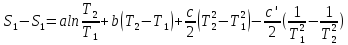
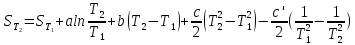
Если требуется определить энтропию при некоторой температуре, а зменение этропии при стандартных условиях известно, то уравнение для химических уравнений будет иметь вид

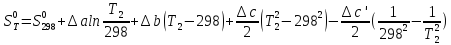
3) Изотермический процесс T=const

,

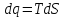
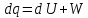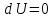
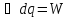
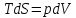
pV=RT

,

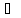
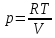
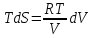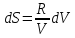
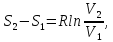
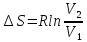
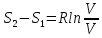
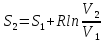
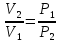
То

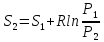
Свободная и связанная энергия.

Свободная энергия Гиббса (G)есть та работа, которую могло бы совершить тело в обратимом изотермическом процессе, или свободная энергия есть максимальная возможная работа, которую может совершить система, обладая каким-то запасом внутренней энергии.

G=U+PV-TS

Существует полезное соотношение, связывающее изменение свободной энергии Гиббса ΔGв ходе химической реакции с её константой равновесия K:

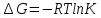
Cвязанная энергия – та часть внутренней энергии, которая не может быть превращена в работу, – это обесцененная часть внутренней энергии.

Внутренняя энергия системы Uравна суммесвободной(F) исвязанной энергии(TS):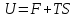

При одной и той же температуре связанная энергия тем больше, чем больше энтропия.

При любом необратимом процессе энтропия увеличивается до того, пока не прекратятся какие-либо процессы, т.е. пока не станет F = 0. И это произойдет при достижении замкнутой системой равновесного состояния, т.е. когда все параметры состояния системы (Р, Т) во всех точках системы станут одинаковыми. Вывести систему из этого равновесного состояния, можно только затратив энергию извне.

7. Основные соотношения между термодинамическими функциями. Уравнение Гиббса-Гельмгольца.

Соответствующие дифференциалы термодинамических потенциалов: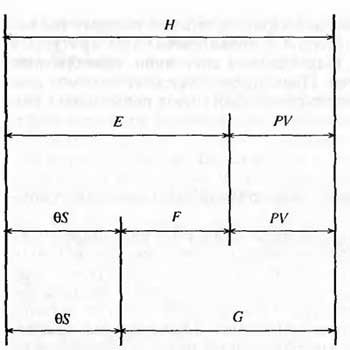

• для внутренней энергии

,

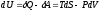• для энтальпии

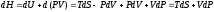
• для свободной энергии Гельмгольца

_,

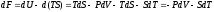• для потенциала Гиббса

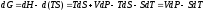
Изохорно-изотермический потенциал. Функции внутренняя энергия U и энтальпия Н редко применяются в химической термодинамике, т.к. условия при которых они характеризуют процесс (V = const, S = const и р = const, S = const) практически неосуществимы. Наибольшее значение имеют характеристические функции: свободная энергия Гельмгольца

F = U - T·S - изохорно-изотермический потенциал и свободная энергия Гиббса

G = H - T·S - изобарно-изотермический потенциал.

Для вывода этих функций воспользуемся обобщенным уравнением I и II законов термодинамики

;

;

;

.

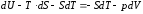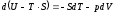Величину U – T ·S обозначим через 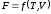, т. е.F=U – T· S. Тогда 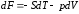. Так какF =f (Т,V) выражается через U и S, то дифференциал её будет полным, т. е.

.

Сравнивая это уравнение с уравнением (2.39), получим:

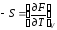и .

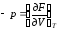Как видно, функция F = U - TS, называемая изохорно-изотермическим потенциалом, также является характеристической.

Изобарно-изотермический потенциал обычно обозначается через G (иногда через Z). Она имеет вид:

Или 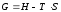, причемG=f(T, р).

Уравнение 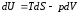и переписываем его в виде:.

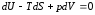К правой и левой частям этого уравнения прибавляем – SdT + Vdp:

.

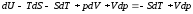В результате 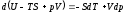. Выражение в скобках естьG=f(T, р), откуда

.

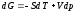Полный дифференциал G=f(T, р)будет

.

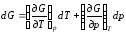Из сравнения этого уравнения с уравнением (2.42) следует, что

; .

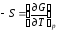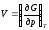Функция 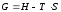называется изобарно-изотермическим потенциалом. Как и все предыдущие функции, она является функцией состояния, т.е. изменение ееΔG = G₂ - G₁ не зависит от пути процесса. Из четырех функцийU=f·(V,S),H= f·(p,S),F= f·(T,V)иG= f·(T,p)в термодинамических расчетах наиболее часто используются функцииF иG, так как они вычисляются по легко измеряемым параметрам (Т,V,p).