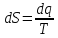Цикл Карно

Сущность ограничений, налагаемых вторым законом на превращение теплоты в работу, можно пояснить на примере действия идеальной машины (машина работает без трения и без потерь тепла, а под рабочим телом подразумевается идеальный газ), работающей по принципу обратимого цикла С. Карно (1824 г).

Рассматриваемый цикл состоит из четырех процессов:

1) изотермического расширения;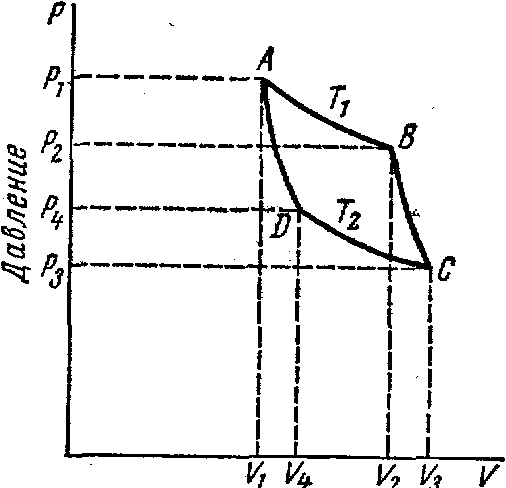

2) адиабатического расширения;

3) изотермического сжатия;

4) адиабатического сжатия газа.

Все процессы проводятся обратимо, в результате чего газ возвращается в исходное состояние. Пусть количество газа равно 1-ому молю. Начальное состояние характеризуется температурой Т₁, давлением p₁, объемом V₁ (точка А на рис.).

В первом процессе газ изотермически и обратимо расширяется от объема V₁ до объема V₂. Допустим, что теплоотдатчик так велик, что его температура заметно не изменяется. В таком процессе газ производит работу расширения А₁ цели­ком за счет поглощения теплоты Q₁.

Тогда .

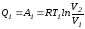Прекратив в точке В подачу тепла, дадим газу адиабатически расшириться. Работа А₂, совершаемая при таком расширении, происходит целиком за счет уменьшения внутренней энергии газа, т. е. понижения его температуры. Последняя падает от Т₁ до Т₂. Объем газа в точке С будет 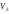. Изменение внутренней энергии в этих условиях

.

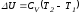Работа в этом процессе в точности равна убыли внутренней энер­гии 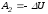, откуда

.

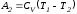От точки С до точки D проводим изотермическое сжатие (теплота отводится в холодильник). При изотермическом сжатии внутренняя энергия газа не изменяется, ибо температура Т₂ постоянна. Вся работа А₃, затрачиваемая на сжатие, переходит в теплоту Q₂, которая и отводится в холодильник. Таким образом,

.

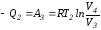Последний процесс - адиабатическое сжатие газа - проведем следующим образом: отсоединим газ от теплоприемника и сожмем его до объема 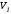, т. е. вернем

газ в исходное состояние. В этом процессе внутренняя энергия газа возрастет на величину, равную затрачен­ной работе сжатия А₄:

; ,

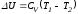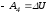т.е. .

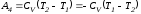Так как процесс в целом является круговым, то внутренняя энер­гия газа в конечном состоянии равна таковой в начальном состоянии, и общее количество теплоты, полученное газом, равно общему количеству произведенной им работы

.

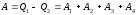А₂ и А₄ равны по абсолютному значению, но противоположны по знаку. Учитывая это, получим: 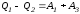. Подставив вместо А₁ и А₃ соответствующие им значения, получим:

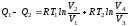или

.

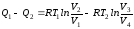Используя уравнение адиабаты 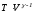= соnst, где 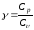, можно доказать, что

,

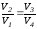тогда .

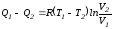Разделив левую и правую части этого равенства на уравнение (2.1), будем иметь:

; ,

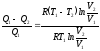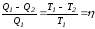где η – коэффициент полезного действия (К.П.Д.) тепловой машины.

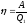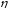Отсюда видно, что коэффициент полезного действия цикла зависит только от разности температур нагревателя и холодильника. Так какТ₂<Т₁, то <1. Следовательно, даже в идеальном случае существует предел превращения теплоты в работу.

Можно доказать, что тепловая машина, работающая по любому реальному циклу, будет иметь коэффициент полезного действия меньше, чем работающая по циклу Карно.

6. Энтропия как мера неупорядоченности системы. Свободная и связанная энергия. Расчет изменения энтропии при различных термодинамических процессах и при протекании химических реакций.

Энтропия как мера неупорядоченности системы.

Энтропия (S)–это мера неупорядоченности движения материи или мера деградации (рассеянности) энергии.

Всякая система со временем переходит из неравновесного состояния в равновесное, в процессе такого перехода энтропия всегда увеличивается, а в состоянии равновесия имеет малое значение.

Размерность энтропии совпадает с размерностью теплоемкости, однако, теплоемкость и энтропия – не одно и тоже. Теплоемкость характеризует количество теплоты, необходимо для нагревания тела на 1 град, а энтропия характеризует количество рассеянной энергии, приходящийся на 1 град. Энтропия является величиной экстенсивной.