5. Обратимые и необратимые, самопроизвольные и несамопроизвольные процессы. Второй закон термодинамики, его формулировки и математическое выражение. Цикл Карно. Обратимые и необратимые процессы

Все процессы, в которых один вид энергии преобразуется в другой, строго подчиняются первому закону термодинамики. Однако этот закон ничего не говорит о направлении процесса. Так первому закону не противоречит переход теплоты от горячего тела к холодному и наоборот. Однако, на опыте наблюдается только самопроизвольный переход теплоты от горячего тела к холодному. Точно также происходит диффузия молекул в направлении от более высокой концентрации к низкой. Все эти процессы протекают самопроизвольно. Такие процессы называются необратимыми или естественными.

После протекания необратимого процесса систему можно вернуть в исходное состояние только путем каких-либо изменений в ней самой или окружающей среде. Во время течения процесса происходят невосполнимые потери энергии в виде теплоты, поэтому работа, произведенная системой при самопроизвольном (естественном) процессе, меньше работы, затраченной на возвращение системы в исходное состояние. Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.

Обратимыми называются процессы, которые могут идти как в прямом, так и в обратном направлениях при бесконечно малом изменении действующих на систему сил и без изменения работоспособности системы в обоих направлениях.

Второй закон термодинамики, его формулировки

Все процессы, происходящие в окружающем нас мире, можно разделить на три группы:

• процессы, для совершение которых требуется затрата работы извне;

• процессы, для совершения которых не требуется затрата работы извне и в результате которых не может быть получена работа против внешних сил;

• процессы, которые могут протекать самопроизвольно, т. е. без затраты работы извне, причем в результате их может быть получена работа против внешних сил.

Второй закон термодинамики определяет:

• какие из процессов в системе при данных условиях (Т, р, С и пр.) могут протекать самопроизвольно (без затраты работы извне);

• каково количество работы, которая может быть получена при этом;

• каков предел возможного самопроизвольного течения процесса (т. е. каково состояние равновесия в данных условиях).

Второй закон термодинамики, также как и первый, был установлен как постулат, обоснованный большим опытом, накопленным человечеством. Он формулируется по-разному. В качестве одной из формулировок принят постулат Клаузиуса (1850):

- теплота не может переходить сама собой от менее нагретого тела к более нагретому;

- невозможен процесс, единственным результатом которого является превращение теплоты в работу;

- невозможно построить такую периодически действующую машину (вечный двигатель второго рода), все действия которой сводились бы к производству работы и соответствующему охлаждению теплового источника.

В теории интегралов доказывается, что если интеграл по замкнутому контуру равен нулю, то подынтегральное выражение является полным дифференциалом некоторой функции от параметров, определяющих состояние системы. Такой функцией является энтропия S, введенная Клаузиусом (1850).

Математической записью второго закона термодинамики для обратимых процессов является:

.
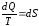