
- •Дисциплина: Физическая химия
- •Работа расширения идеального газа.
- •Теплоемкость при постоянном давлении и объеме и связь между ними.
- •Температурная зависимость теплоемкости от температуры.
- •Применение первого закона термодинамики к химическим процессам.
- •Связь между qp и qv.
- •Расчет тепловых эффектов химических реакций по теплотам образования и теплотам сгорания веществ (на примере реакции).
- •4. Зависимость теплового эффекта от температуры. Уравнение Кирхгоффа в дифференциальной и интегральной форме. Зависимость теплового эффекта от температуры.
- •5. Обратимые и необратимые, самопроизвольные и несамопроизвольные процессы. Второй закон термодинамики, его формулировки и математическое выражение. Цикл Карно. Обратимые и необратимые процессы
- •Второй закон термодинамики, его формулировки
- •Цикл Карно
- •Расчет изменения энтропии при различных термодинамических процессах и при протекании химических реакций.
- •Свободная и связанная энергия.
- •7. Основные соотношения между термодинамическими функциями. Уравнение Гиббса-Гельмгольца.
- •Уравнение Гиббса – Гельмгольца
- •Вывод дифференциальной формы уравнения Клаузиуса - Клапейрона для процесса кипения.
- •Интегрирование уравнения Клаузиуса - Клапейрона и его анализ.
- •Признаки равновесных состояний.
- •Закон действующих масс. Вывод константы равновесия для гомогенной реакции.
- •Связь между различными формами выражения констант равновесия.
- •Химическое сродство как мера реакционноспособности системы. Изотерма Вант-Гоффа.
- •Нормальное химическое сродство.
- •11. Зависимость константы равновесия от температуры. Уравнение изобары Вант-Гоффа в дифференциальной и интегральной формах. Уравнение изохоры Вант-Гоффа в дифференциальной и интегральной формах.
- •Метод Темкина–Шварцмана
- •13. Термодинамика и законы разбавленных растворов. Понижение давления пара растворителя над раствором. Закон Рауля.
- •14. Растворимость газов в жидкостях. Закон Генри. Зависимость растворимости газов от различных факторов.
- •15. Замерзание и кипение растворов. Криоскопия и эбуллиоскопия.
Теплоемкость при постоянном давлении и объеме и связь между ними.
Теплоёмкость не является функцией состояния, она определяется характером процесса. В зависимости от условий проведения процесса различают изохорную (Сv) и изобарную (Ср) теплоёмкости. Для идеального газа:
Сν
=
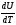 ;
Ср =
;
Ср =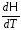 .
.
Для других систем используются частные производные:
Сν
=
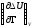 ; Ср =
; Ср =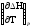 .
.
Связь между Ср и Сv определяется уравнением Р. Майера.
Ср - Сν = R.
где R – универсальная газовая постоянная.
В теплотехнике широко применяется отношение теплоемкостей k = Ср/Сν, которое носит название коэффициента Пуассона (показателя адиабаты).
Температурная зависимость теплоемкости от температуры.
Температура значительно влияет на величину теплоёмкости и это влияние различно в различных температурных интервалах. Температурную теплоёмкость можно схематично рассмотреть на графике.
Рис.
Зависимость теплоёмкости от температуры.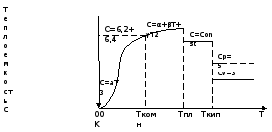
Ткомн – стандартная температура, 298 К.
I область. (0К–298К) зависимость описывается уравнением Дебая:
С = аТ3
При Т0=298К теплоёмкость определяется правилом Дюлонга-Пти: Атомная теплоёмкость элементов в твёрдом состоянии есть величина приблизительно одинаковая для всех элементов и в среднем равная
Сат = 6,2 6,4 кал/ г-атомград.
или Сат = 25,9 26,7 Дж/г-атомград.
Для молекул Нейманом и Коппом сформулировано правило аддитивности: молярная теплоёмкость равна сумме теплоёмкости атомов, входящих в состав вещества.
См = Сат.
См = М·Суд = n·(25,9 26,7) Дж/ моль·град.
II область: (298 К – Тпл) Зависимость теплоёмкости от температуры выражается степенным рядом:
Ср = а + вТ + сТ2;
Ср = а + вТ + с’ Т-2;
Ср = а + вТ + сТ2 + dТ3.
где а, в, d, с, с’ – эмпирические температурные коэффициенты теплоёмкости.
III область: (Тпл-Ткип) Для жидкого состояния теплоёмкость характеризуется в целом величиной меньшей, чем для твёрдого состояния и остаётся величиной постоянной во всем интервале температур.
IV область: (выше Ткип) В этом случае теплоёмкость газообразного состояния вещества также остаётся величиной постоянной и ещё меньшей, чем в жидком состоянии. Для одноатомных металлов в газообразном состоянии теплоёмкость определяется величинами:
Сv = 3 кал / г-атомград = 12,54 Дж/ г-атомград,
Ср = 5 кал / г-атомград = 20,9 Дж/ г-атомград.
3. Закон Гесса и следствия из него. Применение первого закона термодинамики к химическим процессам. Связь между qp и qv. Расчет тепловых эффектов химических реакций по теплотам образования и теплотам сгорания веществ (на примере реакции).
Закон Гесса
В 1836 г. Г. И. Гесс открыл основной закон термохимии, который является частным случаем первого закона термодинамики применительно к химическим реакциям, протекающим в изохорных или изобарных условиях. Закон Гесса устанавливает: если из данных исходных веществ можно получить заданные конечные вещества различными путями, то суммарная теплота на одном каком-нибудь пути равна суммарной теплоте процесса на другом пути, т.е. тепловой эффект химических реакций зависит только от начального и конечного состояния системы, но не зависит от пути перехода.
Из закона Гесса выводится ряд следствий:
I следствие:Тепловой эффект разложения какого-либо соединения равен по величине, но противоположен по знаку тепловому эффекту образования этого соединения.
Н разл. = - Н обр.
6Сграфит+ 3Н2(газ)= С6Н6 (жид.)+ 49 кДж
Теплотой разложенияхимического соединения называется тепловой эффект разложения одного моля сложного вещества на простые вещества вих устойчивых соединениях при стандартных условиях
С6Н66С + 3Н2- 49 кДж
II следствие:Тепловой эффект химической реакции равенразностиалгебраических сумм теплот образования продуктов реакции и исходных веществ.
Так для реакции общего типа:
аА + bBсС +dД
Тепловой эффект рассчитывается по уравнению:
Нхр = [сНобр. (С) +dНобр.(D)] - [a Нобр. (A) + b Нобр. (B)].
Если энтальпия (теплота образования) измеряется при стандартных условиях:
Р = 101 325 Па и Т = 25 0С = 2980К, то обозначаетсяН0298.
III следствие: Тепловой эффект химической реакции равен разности сумм теплот сгорания исходных веществ и продуктов реакции.
Для вышеуказанной реакции общего типа тепловой эффект равен:
Нхр = [аНсгор. (А) + вНсгор. (В)] - [сНсгор. (С) +dНсгор. (D)].
2С6Н6 + 15О212 СО2 + 6Н2О
С6Н6 + 15/2О26 СО2 + 3Н2О +Нсгор.
Теплоту сгорания с точностью до (0,01 %) можно определить калориметрическим методом или рассчитать по формуле Д. П. Коновалова:
Qсг. = 204,2n+ 44m+x,
где n– число атомов кислорода необходимых для полного сгорания 1 моля вещества; m – число молей воды;x– термическая характеристика, является функцией связей или групп атомов.
IV следствие:Если две реакции имеют одинаковое начальное состояние, но различное конечное, то разность их тепловых эффектов равна тепловому эффекту перехода из одного конечного состояния в другое.
С + 1/2 О2СО - Н1
С + О2СО2 - Н
Для СО + 1/2 О2СО2 - Н2
Н2 = Н - Н1
V следствие: Если две реакции из различных начальных состояний переходят к одному конечному состоянию, то разность их тепловых эффектов равна тепловому эффекту перехода одного начального состояния в другое.
С + О2СО2 - Н
СО + 1/2 О2СО2 - Н2
С + 1/2 О2СО - Н1
Н1 = Н - Н2
