
- •Дисциплина: Физическая химия
- •Работа расширения идеального газа.
- •Теплоемкость при постоянном давлении и объеме и связь между ними.
- •Температурная зависимость теплоемкости от температуры.
- •Применение первого закона термодинамики к химическим процессам.
- •Связь между qp и qv.
- •Расчет тепловых эффектов химических реакций по теплотам образования и теплотам сгорания веществ (на примере реакции).
- •4. Зависимость теплового эффекта от температуры. Уравнение Кирхгоффа в дифференциальной и интегральной форме. Зависимость теплового эффекта от температуры.
- •5. Обратимые и необратимые, самопроизвольные и несамопроизвольные процессы. Второй закон термодинамики, его формулировки и математическое выражение. Цикл Карно. Обратимые и необратимые процессы
- •Второй закон термодинамики, его формулировки
- •Цикл Карно
- •Расчет изменения энтропии при различных термодинамических процессах и при протекании химических реакций.
- •Свободная и связанная энергия.
- •7. Основные соотношения между термодинамическими функциями. Уравнение Гиббса-Гельмгольца.
- •Уравнение Гиббса – Гельмгольца
- •Вывод дифференциальной формы уравнения Клаузиуса - Клапейрона для процесса кипения.
- •Интегрирование уравнения Клаузиуса - Клапейрона и его анализ.
- •Признаки равновесных состояний.
- •Закон действующих масс. Вывод константы равновесия для гомогенной реакции.
- •Связь между различными формами выражения констант равновесия.
- •Химическое сродство как мера реакционноспособности системы. Изотерма Вант-Гоффа.
- •Нормальное химическое сродство.
- •11. Зависимость константы равновесия от температуры. Уравнение изобары Вант-Гоффа в дифференциальной и интегральной формах. Уравнение изохоры Вант-Гоффа в дифференциальной и интегральной формах.
- •Метод Темкина–Шварцмана
- •13. Термодинамика и законы разбавленных растворов. Понижение давления пара растворителя над раствором. Закон Рауля.
- •14. Растворимость газов в жидкостях. Закон Генри. Зависимость растворимости газов от различных факторов.
- •15. Замерзание и кипение растворов. Криоскопия и эбуллиоскопия.
Метод Темкина–Шварцмана
Для практических целей приходится константу равновесия вычислять при температурах более высоких, чем стандартные. Для этого необходимо знать ΔGТ0, ΔНТ0 и ΔST0.
Значительные сокращения математических операций при подсчете указанных величин достигаются методом, предложенным М. И. Темкиным и Л. А. Шварцманом. Возьмем определенный интервал из уравнения Кирхгофа (1.33) в пределах от 298 до Т К, при этом получим
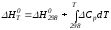 .
(1)
.
(1)
Для
расчета изменения энтропии химической
реакции проинтегрируем в тех же пределах
уравнение
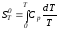 ,
где вместо теплоемкости одного вещества
следует подставить изменение теплоемкости
ΔСр
системы:
,
где вместо теплоемкости одного вещества
следует подставить изменение теплоемкости
ΔСр
системы:
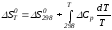 .
(2)
.
(2)
Значения
(1) и (2) подставляем в уравнение
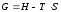 :
:
ΔGT0 = ΔНТ0 -Т ΔST0.
При этом получим
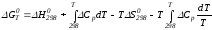 .
.
Подставим в подынтегральные выражения эмпирический степенной ряд:
ΔСр = Δа + Δв Т + ΔсТ2,
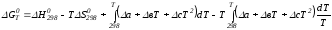 .
.
Интегрируя, получим
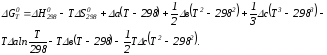
Раскроем скобки:
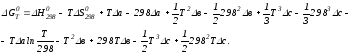
Сгруппируем члены относительно температурных коэффициентов Δа; Δв и Δс:

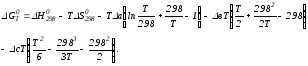
Обозначим:
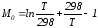 ;
;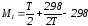 ;
;
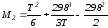 ;
;
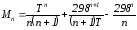 .
.
Подставив Мi в уравнение (4.22), получим
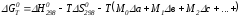 .
.
Выражение для Мn справедливо, начиная с М1. Коэффициенты М0… Мnзависят только от температуры. Они рассчитаны и представлены в справочной литературе.
13. Термодинамика и законы разбавленных растворов. Понижение давления пара растворителя над раствором. Закон Рауля.
Среди растворов особенно интересны
такие, для которых во всей области
концентраций соблюдается простейшая
линейная зависимость парциальных и
общего давлений пара от концентрации.
Если концентрацию выражать в мольных
долях, то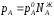 ;
;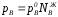 ;
(1)
;
(1)
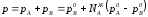 ;
;
где
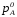 и
и
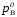 -
давления насыщенного пара чистых
компонентов А и В при данной температуре;
-
давления насыщенного пара чистых
компонентов А и В при данной температуре;
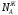 и
и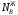 - мольные доли компонентов в жидкой
фазе.
- мольные доли компонентов в жидкой
фазе.
Уравнения (1) являются математическим выражением закона Рауля, согласно которому при постоянной температуре парциальное давление napа каждого компонента равно давлению пара этого компонента в чистом виде, помноженному на его мольную долю в растворе.
Для бинарного раствора, состоящего из компонентов А и В (А - растворитель) удобнее использовать другую формулировку: Относительное понижение парциального давления пара растворителя над раствором не зависит от природы растворённого вещества и равно его мольной доле в растворе.
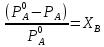
Растворы
двух летучих веществ, подчиняющиеся
закону Рауля во всей области концентраций
от
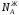 =
0 до
=
0 до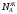 =
1,называются
идеальными
растворами.
Этот тип растворов встречается редко.
Идеальные растворы могут образовывать
вещества, молекулы которых сходны по
полярности, строению, химическому
составу и, следовательно, взаимодействуют
между собой с такой же силой FА-В,
с какой взаимодействуют молекулы в
чистых компонентах (FА-В
=
FА-А=
FВ-В).
Именно этим можно объяснить зависимость
давления насыщенного пара над идеальным
раствором только от концентрации, а
также тот факт, что
идеальные
растворы
образуются из жидких компонентов без
выделения и поглощения теплоты (
=
1,называются
идеальными
растворами.
Этот тип растворов встречается редко.
Идеальные растворы могут образовывать
вещества, молекулы которых сходны по
полярности, строению, химическому
составу и, следовательно, взаимодействуют
между собой с такой же силой FА-В,
с какой взаимодействуют молекулы в
чистых компонентах (FА-В
=
FА-А=
FВ-В).
Именно этим можно объяснить зависимость
давления насыщенного пара над идеальным
раствором только от концентрации, а
также тот факт, что
идеальные
растворы
образуются из жидких компонентов без
выделения и поглощения теплоты (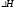 =0)
и без изменения объема (υ=0), т. е. объем
полученного раствора равен сумме объемов
компонентов.
=0)
и без изменения объема (υ=0), т. е. объем
полученного раствора равен сумме объемов
компонентов.
Растворы, образованные без изменения объема и энтальпии компонентов, близких по свойствам, часто называют совершенными.
Изотермическая
диаграмма х,
р
для идеальных растворов изображена на
рис. В соответствии с уравнениями
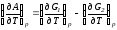 и
и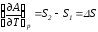 она
состоит из трех прямых.
она
состоит из трех прямых.
Т=const
Рис.1. Зависимость парциальных и общего давлений пара от состава для идеального раствора
Для реальных растворов данные зависимости являются криволинейными. Если молекулы данного компонента взаимодействуют друг с другом сильнее, чем с молекулами другого компонента, то истинные парциальные давления паров над смесью будут больше, чем вычисленные по первому закону Рауля (положительные отклонения). Если же однородные частицы взаимодействуют друг с другом слабее, чем разнородные, парциальные давления паров компонентов будут меньше вычисленных (отрицательные отклонения). Реальные растворы с положительными отклонениями давления пара образуются из чистых компонентов с поглощением теплоты (ΔНраств > 0), растворы с отрицательными отклонениями образуются с выделением теплоты (ΔНраств < 0).
Рис.
2. Зависимость
парциальных и общего давлений пара
идеальных (штриховая линия) и реальных
(сплошная линия) бинарных растворов от
состава при положительных (слева) и
отрицательных (справа) отклонениях от
закона Рауля.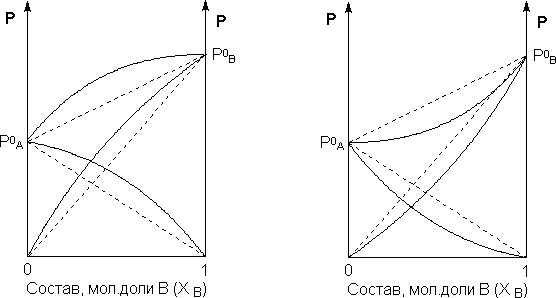
Второй закон Рауля является следствием из первого. Второй закон Рауля можно в наиболее общем виде сформулировать следующим образом: Понижение температуры замерзания и повышение температуры кипения разбавленного раствора нелетучего вещества прямо пропорционально моляльной концентрации раствора и не зависит от природы растворенного вещества.
Данный
закон справедлив только для бесконечно
разбавленных растворов. Коэффициенты
пропорциональности в уравнениях
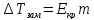 и
и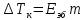 – криоскопическая и эбулиоскопическая
константы – имеют физический смысл
соответственно повышения температуры
кипения и понижения температуры
замерзания растворов с моляльной
концентрацией, равной 1 моль/кг. Однако,
поскольку такие растворы не являются
бесконечно разбавленными, эбулиоскопическая
и криоскопическая константы не могут
быть непосредственно определены и
относятся поэтому к числу т.н.
экстраполяционных констант.
– криоскопическая и эбулиоскопическая
константы – имеют физический смысл
соответственно повышения температуры
кипения и понижения температуры
замерзания растворов с моляльной
концентрацией, равной 1 моль/кг. Однако,
поскольку такие растворы не являются
бесконечно разбавленными, эбулиоскопическая
и криоскопическая константы не могут
быть непосредственно определены и
относятся поэтому к числу т.н.
экстраполяционных констант.
Зависимость растворимости газов в жидкости определяется законом Генри:
Растворимость газа в жидкости прямо пропорциональна парциальному давлению газа при постоянной температуре
C=Г·P
где P - давление пара растворенного вещества,C - мольная доля его, Г - постоянная Генри.
