Нормальное химическое сродство.

Для того, чтобы можно было сравнивать сродство различных веществ, было введено понятие нормального химического сродства. К уравнению нормального химического сродства легко перейти из уравнения изотермы Вант-Гоффа, если предположить, что исходные концентрации или исходные парциальные давления всех участников реакции равными единице, тогда уравнения изотермы Вант-Гоффа упростятся и убыль нормальной свободной энергии примет вид:

G⁰=W_р=RTlnK_p,

F⁰=W_v=RTlnK_c.

где G⁰иF⁰–нормальное химическое сродство или мера химического сродства. Сравнивая W_vи W_pразличных веществ, можно получить характеристику степени их удалённости от состояния равновесия при концентрации каждого из них С_i= 1 моль/л или парциальном давлении Р_i= 1атм.

11. Зависимость константы равновесия от температуры. Уравнение изобары Вант-Гоффа в дифференциальной и интегральной формах. Уравнение изохоры Вант-Гоффа в дифференциальной и интегральной формах.

Зависимость константы химического равновесия от температуры выводится, во-первых, из уравнения нормального химического сродства:

- G⁰=W_р=RTlnKp,

и, во- вторых, из уравнения Гиббса-Гельмгольца:

G⁰_Т = H⁰_Т –TS⁰,

G⁰_Т=H⁰_Т–T,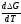

удобно сочетающих первый и второй законы термодинамики применительно к обратимым изотермическим процессам, где Н⁰_Т– тепловой эффект реакции, Дж/моль,S⁰– изменение энтропии, Дж/мольК.

Для нахождения зависимости константы химического равновесия от температуры возьмём производную по температуре из уравнения изотермы и подставив значение G и её производной по температуре в уравнение (4.22), получим уравнение:

- RTlnKp=H⁰_Т–RTlnKp–RT².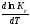

Сократив одинаковые члены уравнения и сделав соответствующие преобразования, получим:

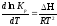, (1)

где 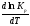– температурный коэффициентконстанты химического равновесия.

Выражение (1) называется уравнением изобары Вант-Гоффа в дифференциальной форме.

Если процесс протекает при постоянном объёме, то зависимость константы равновесия от температуры определяется уравнением изохоры Вант-Гоффа, которое выводится аналогичным образом:

,

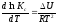где U– стандартное изменение внутренней энергии системы.

Для реакций, протекающих в неидеальных растворах, в уравнении изохоры К_сзаменяется на К_а(концентрация (с) заменяется на активность (а)), при этом получается:

.

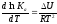Анализ уравнений изобары и изохоры показывает, если реакция протекает с выделением теплоты (H < 0,U < 0), то температурный коэффициент константы равновесия меньше нуля:

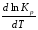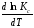< 0;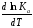< 0;< 0.

Следовательно, с повышением температуры константа равновесия экзотермических реакций уменьшается и равновесие смещается в сторону обратной реакции.

Если Н > 0 иU> 0 реакция протекает с поглощением тепла, т. е. является эндотермической, то:

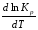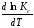> 0;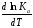> 0;> 0.

Это означает, что с ростом температуры константа равновесия эндотермической реакции всегда увеличивается и равновесие смещается в сторону прямой реакции (вправо). Отсюда вывод: экзотермические реакции необходимо проводить при пониженной, а эндотермические – при повышенной температуре, так как наибольшая полнота эндотермических реакций достигается при возможно более высоких температурах, а наибольшая полнота экзотермических реакций – при более низких температурах. И наконец, еслиН = 0, то константа равновесия Кр не зависит от температуры. Эти же выводы получаются изпринципа смещения равновесия Ле-Шателье-Брауна(1885-1886 гг.):

Если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя какое-либо из условий, определяющих состояние равновесия, то в системе усилится то из направлений процесса, течение которого ослабляет влияние произведённого воздействия, и положение равновесия сместится в том же направлении.

Так в реакции 3Н₂+N₂ 2NH₃ H⁰₂₉₈= - 46,2 кДж/моль

при понижении температуры и повышении давления усиливается экзотермическая реакция синтеза аммиака, сопровождающаяся уменьшением объёма, так как только таким путём может быть ослаблен эффект внешнего воздействия.

Для использования уравнений Вант-Гоффа для практических расчётов следует проинтегрировать дифференциальные уравнения изобары и изохоры в пределах двух температур с учётом того, что тепловой эффект реакции в небольшом температурном интервале изменяется незначительно и его можно считать условно постоянным. При таком допуске интегрирование уравнения (1)

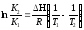. (2)

Уравнение (2) называется интегральной формой изобары Вант-Гоффа, оно позволяет: Во-первых, вычислить стандартный тепловой эффект реакцииН⁰по экспериментально найденным при двух температурах константам равновесия; Во-вторых, вычислить константу равновесия при заданной температуре, если известный стандартный тепловой эффект реакции и константа равновесия при стандартной температуре.

Интегральная форма изобары Вант-Гоффа аналогично:

Более точное значение теплового эффекта реакции, учитывающее его зависимость теплоёмкости от температуры Т, рассчитывается по закону Кирхгофа:

Н⁰_Т=Н⁰₂₉₈+,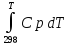

где H⁰₂₉₈- стандартная энтальпия, Дж/моль;Ср – изменение теплоёмкости веществ в процессе реакции.

Неопределённое интегрирование уравнения изобары Вант-Гоффа (4.27) даёт линейное уравнение:

. (3)

При переходе к десятичному логарифму получим:

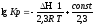. (4)

Обозначим постоянные слагаемые буквами А и В, тогда уравнение примет вид:

lnKp =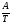+ B. (5)

Выражения (3)-(5) удобны для графического анализа процессов, так как зависимость в координатах lnK_p=f(1/T) представляет собой прямую линию, где А = -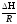- угловой коэффициент прямой, а В =const- отрезок ординаты, отсекаемой этой прямой и равныйlnK_pпри 1/Т = 0.

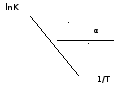
Рис. Зависимость логарифма константы равновесия от величины обратной температуры.

Из уравнения (5) и рисунка видно, что логарифм константы равновесия линейно зависит от обратного значения температуры, при этом, если Н < 0, реакция является экзотермической, прямая на графикеlnK=f(1/T) образует тупой угол и константа равновесия с ростом температуры увеличивается. И, наоборот, еслиН > 0, реакция является эндотермической, угол оказывается острым, константа равновесия увеличивается с понижением температуры.

12. Расчет равновесных состояний с помощью таблиц стандартных термодинамических величин и по методу Тёмкина-Шварцмана

Расчет химического равновесия с помощью таблиц стандартных термодинамических величин

В настоящее время при расчетах химических равновесий широко используют таблицы термодинамических величин, где приведены вычисленные с большой точностью термодинамические характеристики веществ в стандартном состоянии. Газы и растворы в стандартном состоянии считаются идеальными.

Расчет ΔG и К_р целесообразно разделить на два этапа:

1) Сначала вычисляют изменение изобарного потенциала реакции для условий, принятых за стандартные (температура 298, 15⁰К; давление, под которым находится каждое из чистых веществ – 1 атм). Стандартные изменения энтальпии, изобарного потенциала и стандартную энтропию принято обозначать ΔН₂₉₈⁰, ΔG₂₉₈⁰ и ΔS₂₉₈⁰. По величине и знаку ΔG₂₉₈⁰ определяют возможность реакции. Если ΔG₂₉₈⁰ >0 и абсолютное значение ΔG₂₉₈⁰ очень велико, то реакция в стандартных условиях неосуществима и, следовательно, все другие расчеты не имеют смысла.

Обычно в таблицах представлены теплоты образования ΔН⁰ соединений из простых веществ. Очевидно, что ΔН⁰ простых веществ, находящихся в стандартном состоянии, равны нулю.

В таблицах приводится также - ΔG⁰ – убыль энергии Гиббса при образовании одного киломоля вещества из элементов, находящихся в стандартном состоянии. Для элементов в стандартном состоянии ΔG⁰ =0.

В термодинамических таблицах приводятся еще абсолютные значения энтропии ΔS⁰ веществ в стандартном состоянии.

Для иллюстрации рассчитаем в общем виде ΔН₂₉₈⁰, ΔG₂₉₈⁰ и ΔS₂₉₈⁰ реакции.

NH₃ + HCl ↔NH₄Cl;

,

,

.

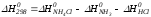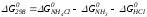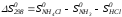2) Затем от найденного значения ΔG₂₉₈⁰ переходят к значению ΔG_Т⁰ при температуре, отличной от температуры 298⁰ К; далее определяют константу равновесия, состав равновесной смеси и выход продуктов реакции.

В соответствии с уравнением (2.41) ΔG_Т⁰ = ΔН_Т⁰ - ТΔS ⁰ для перехода от ΔG₂₉₈⁰ к ΔG_Т⁰ необходимо пересчитать ΔН₂₉₈⁰ на ΔН_Т⁰ и ΔS₂₉₈⁰ на ΔS_Т ⁰для заданной температуры.

Чтобы определить значения термодинамических характеристик при других температурах и давлениях, надо использовать выведенные ранее соотношения.