Интегрирование уравнения Клаузиуса - Клапейрона и его анализ.

Интегрирование уравнения Клапейрона-Клаузиуса в пределах температур Т₁ и Т₂, которым соответствуют давления P₁ и P₂ при =const, дает:

,

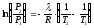После преобразования последнего получают аналитическую форму уравнения Клапейрона-Клаузиуса:

.

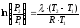Полученное выражение даёт возможность определить:

- неизвестное давление по известным температурам, другому давлению и

теплоте кипения и известному давлению: ;

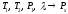- неизвестное температуру кипения, по известным давлениям, теплоте кипения и другой температуре: ;

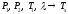- теплоту кипения , если известны при двух давлениях насыщенного пара температуры кипения :

.

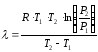
Неопределённое интегрирование уравнения (5.9) с учётом того, что теплота кипения не зависит от температуры даст уравнение:

или .

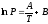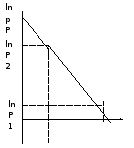
Выражения представляют уравнения прямой линии с угловым коэффициентом А в координатах 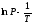(рис.).

Рис. Зависимость давления насыщенного пара от температуры.

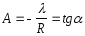
По тангенсу угла наклона прямой можно определить теплоту испарения:

_граф =  Rtg.

Чем больше угол , тем больше теплота испарения, и следовательно, тем быстрее испаряется жидкость. Тангенс угла находят из соотношения:

.

Определив теплоту кипения вещества аналитически и графически, можно рассчитать приращение энтропии в процессе кипения:

.

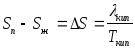9. Химическое равновесие. Классификация равновесных состояний. Признаки равновесных состояний. Закон действующих масс. Вывод константы равновесия для гомогенной реакции. Связь между различными формами выражения констант равновесия.

Химическое равновесие. Классификация равновесных состояний.

Химическая система находится в равновесии, если её состояние при заданных внешних условиях (например, температуре и давлении) во времени не изменяется. Различают три вида равновесия:

- стабильное (устойчивое или истинное);

- лабильное (неустойчивое);

- метастабильное (относительно устойчивое).

Стабильное равновесие характеризуется абсолютным минимумом энергетических характеристических функций. При таком равновесии система, выведенная из равновесия достаточно малым воздействием, самопроизвольно возвращается в исходное состояние после прекращения воздействия на неё.

Лабильное равновесие характеризуется тем, что при любом бесконечно малом воздействии система претерпевает такие изменения, в результате которых она переходит в стабильное состояние.

Метастабильное равновесие характеризуется относительным минимумом характеристических функций. В этом случае воздействие на систему может привести к конечному изменению в направлении стабильного равновесия, однако, некоторые бесконечно малые изменения вызывают настолько малые изменения в системе, что после прекращения этих воздействий система возвращается в исходное состояние.

Равновесие не означает полного покоя в системе. Напротив, при равновесии в системе идут процессы очень энергично, но в противоположных направлениях. С этой точки зрения химическое равновесие является динамичным (подвижным) равновесием.

Таким образом, истинное химическое равновесное состояние характеризуется неизменностью состава, подвижностью (динамичностью) и абсолютным минимумом значений характеристических термодинамических функций: G, F.

Пределом самопроизвольного протекания реакции при определённых условиях является достижение химического равновесия.

Теоретически все химические реакции в большей или меньшей степени обратимы, т. к. в одних и тех же условиях могут протекать в противоположных направлениях. Реакции, сопровождающиеся образованием вещества, выбывающего из участников реакции (образование осадков, газов, малодиссоциируемых веществ, комплексных соединений) называются практически необратимыми, так как скорость обратной реакции столь мала, что не поддаётся измерению.

Обратимые реакции никогда не доходят до конца, т. е. до полного исчезновения исходных веществ и превращения их в продукты.