Решение

1. Определим реакции на опорах, считая, что усилие Qприложено статически

; ,

,,

; , ,.

Проверим правильность определения реакций:

, , 50– 100 + 50 = 0, 0 = 0.

2. Определим опасное сечение в балке (случай статического нагружения, см. рис. 39).

1-й участок: 0 ≤х≤ ℓ/2,, .

При х = 0; ;М = 0.

При х=ℓ/2; ; .

2-й участок: 0 ≤ х ≤ℓ/2, , .

При х= 0; ;М= 0.

При x=ℓ/2; , .

Построим эпюры QиМ. Опасное сечение –С(рис. 38).

,

Тогда .

3. Определим коэффициент динамичности из выражения:

.

Определим статическое перемещение точки соударения С, используя метод Максвелла–Мора.

Реакции на опорах грузовой и единичной схемы равны (рис. 40):

, .

.

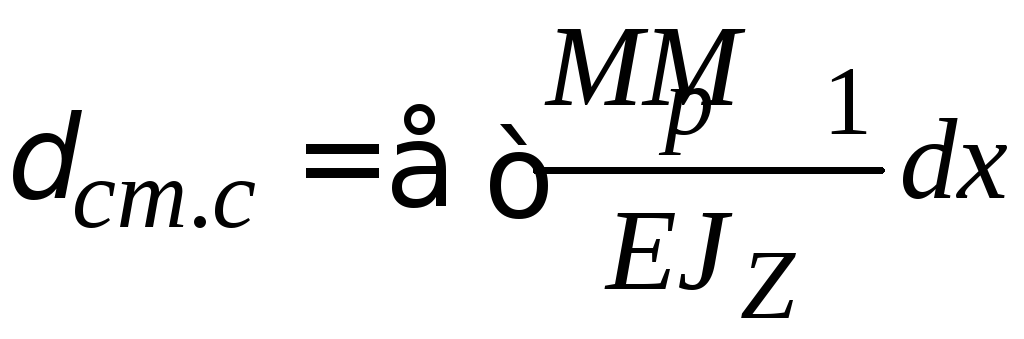1-й участок: 0 ≤ х≤ℓ/2; , .

2-й участок: 0 ≤ х≤ℓ/2 ,

Так как ,

Тогда статическое перемещение точки контакта падающего груза (точка С, рис. 40) определяется из уравнения:

.

Здесь учтено, что для двутавра № 10I_z = 198 см⁴.

Коэффициент динамичности: , то есть величины статических прогибов и напряжений при ударном приложении нагрузки возрастут в 86,9 раза.

Динамический прогиб в точке удара: δ_дин = δ_статичК_д= 0,0053 ×86,9 = 0,46 мм.

Проверим прочность балки в опасном сечении.σ_max≤ [σ].

86,9×50/(39,7×10^-6) = 109×10⁶Па = 109 МПа ≤ 160 МПа.

Условие прочности выполняется.

З А Д А Ч А № 11

Расчет на прочность вращающегося вала

Таблица 10
№ варианта	d, мм	l, мм	[σ], МПа
1	30	240	80
2	32	250	85
3	35	260	90
4	38	270	95
5	40	280	100
6	42	290	105
7	45	300	110
8	48	310	115
9	50	320	120
10	52	330	125
11	55	35	130
12	30	260	90
13	35	270	95
14	40	300	150
15	42	260	90
16	45	320	120
17	50	300	110
18	52	320	120
19	48	300	110
20	52	300	100

С круглым стальным валом (рис. 41) жестко соединен ломаный стержень такого же диаметра (d). Сила тяжести единицы объема материала вала и стержня γ= 0,078 н/см³. Требуется:

1. определить силы инерции, действующие на отдельные участки ломаного стержня и на вал при равномерном вращении вала;

2. построить эпюру изгибающих моментов для всех участков ломанного стержня и вала и определить опасное сечение;

3. найти допускаемую угловую скорость вращения вала (ω) из условия прочности на изгиб, если допускаемое напряжение для материала вала равно [σ].

Исходные данные взять из табл. 10.

Пример выполнения задачи № 11

Определить допустимую угловую скорость вращения вала ω (рис. 42). Исходные данные: [σ] = 120МПа; γ = 78кН/м³; d = 60мм; l = 400мм.

Решение:

Определим инерционные нагрузки и построим эпюру изгибающих моментов.

Инерционная нагрузка будет складываться из изгибающих моментов участков АВ, ВС, CD, CE и растягивающей нагрузки участка ВС.

При вращении участка АВ будет равномерно распределена по его длине с интенсивностью , здесь (рис. 43):

- масса единичной длины;

- площадь поперечного сечения;

- радиус вращения;

;

- центростремительное (нормальное) ускорение.

Растягивающая сила участка ВС может быть определена интегрированием:

.

Для построения изгибающих моментов (растягивающими усилиями и напряжениями растяжения – сжатия можно пренебречь) достаточно выделить 3 участка АВ, ВС,CD (в конце участка DE в точке Е момент равен 0) с движением со свободного конца (рис. 44).

; ; ;

; .

;

;

;

;

.

З А Д А Ч А № 12

Расчет на усталость

Стальной ступенчатый вал диаметрами D и d и радиусом галтели r (рис. 45) испытывает переменный изгиб с кручением: нормальные напряжения  изменяются от _max до _min; касательные  – от _max до _min ; вал подвергнут тонкой обточке; материал – сталь. Исходные данные согласно варианту приведены в табл. 11.

Определить запас прочности вала.