Пример выполнения задачи № 9

Дано: расчетная схема на рис. 29.

Решение:

1. Построение эпюр ВСФ.

1-й участок:

Рис. 29

.

2-й участок: .;

при

при

.

Эпюры построены на рис. 30.

Опасное сечение по - в заделке .

.

Выбираем двутавр № 24:

масса 1м = 27,3кг.

Проверим прочность по τ_max. Опасное сечение в заделке .

Проверим прочность с учетом продольного усилия N. Опасное сечение – где М и N одновременно имеют значительную величину. Приоритет отдается величине М.

В данном примере N = 0 на всех участках, поэтому проверка не производится.

2. Определим вертикальное перемещение в точке А. Для этого прикладываем в точке А единичную силу (рис. 31), записываем выражения для моментов от действия единичной силы на каждом участке и вычисляем интеграл Мора 1-й участок:

2-й участок:

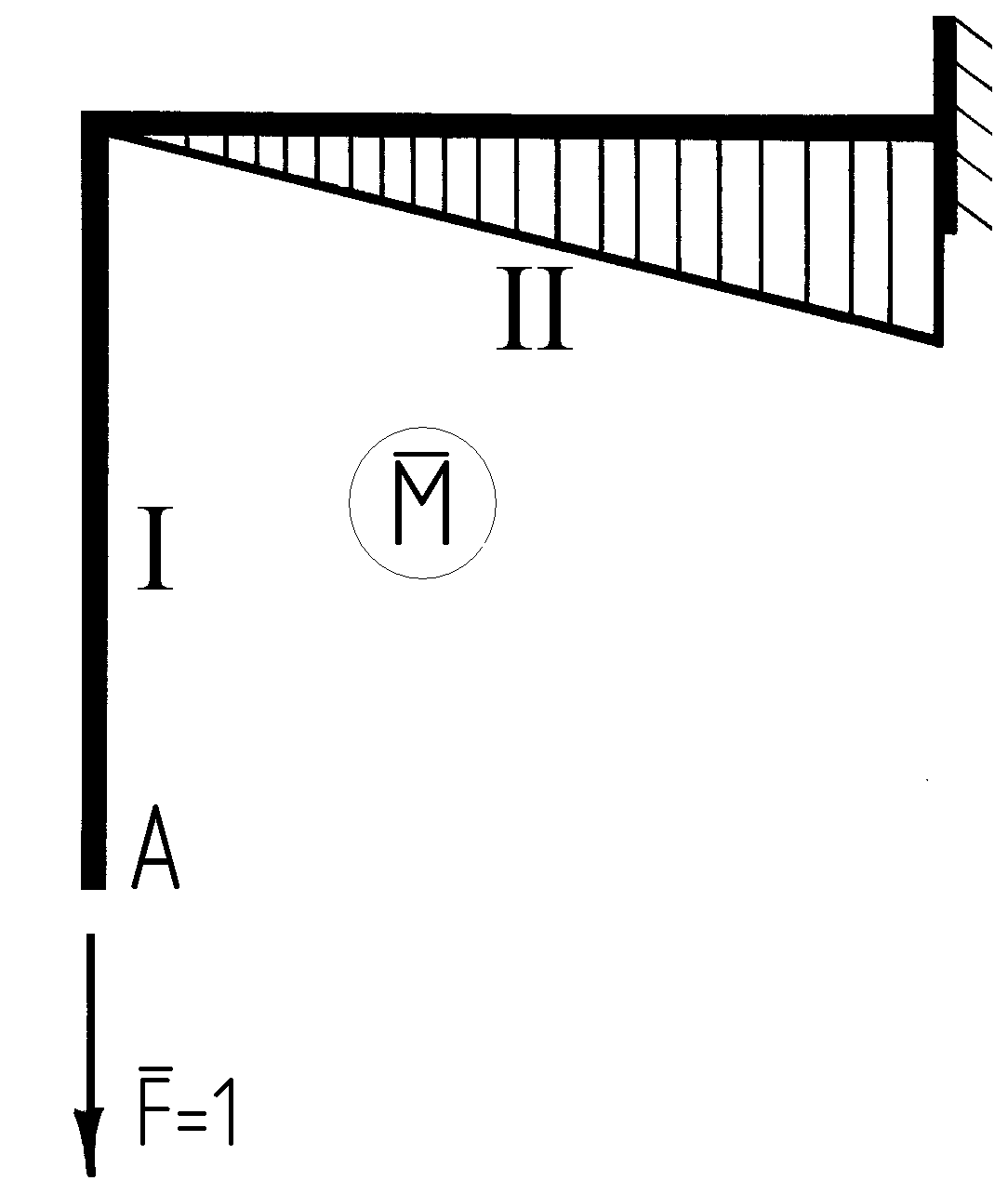
Рис. 31

. Определим угол поворота в точке С. для этого в точке С прикладываем единичный момент (рис. 32).

1-й участок:

2-й участок:

3. Преобразуем статически определимую систему в статически неопределимую. Для этого поставим дополнительную опору (2 связи) (рис. 33). Обращаем внимание на то, что в учебном задании достаточно добавить одну дополнительную связь.

Рис. 33

Эпюры ВСФ от внешней нагрузки в основной системе уже построены для статически определимой системы.

Строим эпюры в основной системе от действия (см. рис. 34).

1-й участок:

2-й участок:

1-й участок:

2-й участок:

Канонические уравнения метода сил:

Вычисляем коэффициенты и свободный член:

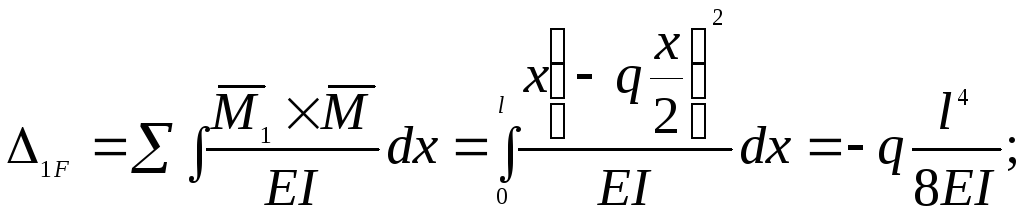
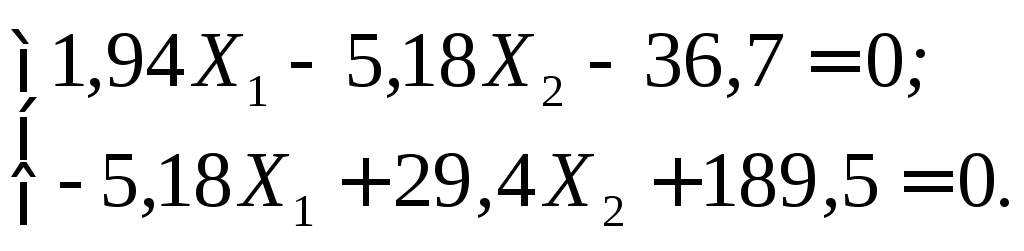
Проверка правильности решения:

а) каждое уравнение системы должно тождественно удовлетворяться при подстановкеX_i .

Для последующей проверки нужно построить результирующие эпюры ВСФ для эквивалентной системы с известными величинами реакций опоры X₁, X₂ (рис. 35).

1-й участок: эпюры на рис. 36.

2-й участок:

Определим

б) продолжаем проверку правильности вычислений. Перемещения в направлении X_i должны быть равны нулю.

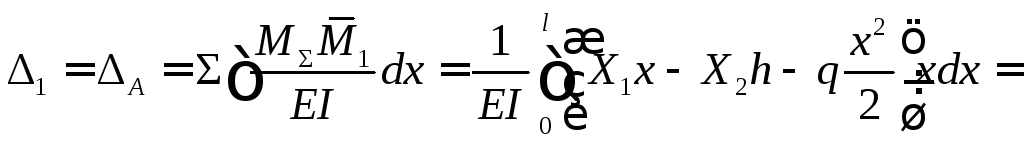
Аналогично для допускается одна суммарная проверка вместо двух представленных выше:

Подбор сечения двутавра производится в опасном сечении по величине изгибающего момента:

Выбираем двутавр № 18:

масса 1м = 18,4кг.

Угол поворота в точке С:

4. Конструкция	Перемещения		Материалоемкость
   	yA, мм	θС, рад	масса 1 м	облегчение
   СОС	5,31		27,3	---
   СНС	0		18,4	33%

   сравнение спроектированных статически определимой и неопределимой систем:

З А Д А Ч А № 10

Расчет на удар

На незагруженную внешними силами упругую балку (рис. 37) с высоты H падает груз Q. Проверить прочность балки при допускаемых напряжениях [σ] = 160 МПа. Определить динамический прогиб в точке удара. Балка изготовлена из двутавра № 10. Массу упругой системы не учитывать.

Расчетная схема выбирается по рис. 37, исходные данные из табл. 9

Пример выполнения задачи № 10

Таблица 9

№ варианта	Q,H	а, м	в, м	h, см	Схема по рис. 37
1	100	1	1,5	2	а
2	50	2	1	3	б
3	60	1	0,5	1	а
4	70	1	1,5	2	б
5	80	2	0,5	3	а
6	90	1	1	2	б
7	120	1	1,5	3	а
8	110	2	1	1	б
9	100	1	0,5	2	а
10	50	1	1,5	3	б
11	60	2	0,5	2	а
12	70	1	1	3	б
13	80	1	1,5	1	а
14	90	2	1	2	б
15	120	1	0,5	3	а
16	110	1	1,5	2	б
17	90	2	0,5	3	а
18	120	1	1	1	б
19	110	1	3	2	а
20	50	2	1	2	б

Дано: Q = 100Н,Н = 0,02м,ℓ =2,0 м. Рис. 38.