Предмет и содержание курса сопротивления материалов

Задачи и методы сопромата.

Все элементы конструкции обладают прочностью и жесткостью.

Задачи сопромата: создание методов оценки прочности.

Сопромат характеризуется приближенными приемами расчета.

1)Объект, модель (расчетная схема), математическая модель

Математическая модель — это математическое представление реальности.

Расчетная схема - это упрощенная, идеализированная схема, которая отражает наиболее существенные особенности объекта, определяющие его поведение под нагрузкой.

Математическое моделирование — это процесс построения и изучения математических моделей.

Все естественные и общественные науки, использующие математический аппарат, по сути, занимаются математическим моделированием: заменяют объект его математической моделью и затем изучают её. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования.

2)Внутренние силовые факторы, уравнения равновесия

В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и передают друг другу их действие.

Внутренние силовые факторы

В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы. По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих сил применяют метод сечений: надо мысленно рассечь брус, находящийся в равновесии, на две части и рассмотреть равновесие одной из них.

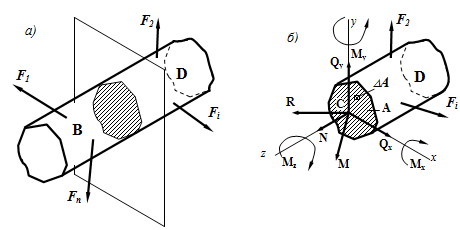
Под действием внешних нагрузок в поперечном сечении бруса возникают следующие внутренние силовые факторы (рис. 2.1):

N_z = N - продольная растягивающая (сжимающая) сила

M_z = T - крутящий (скручивающий) момент

Q_x (Q_y) = Q  - поперечные силы

M_x (M_y) = M - изгибающие моменты

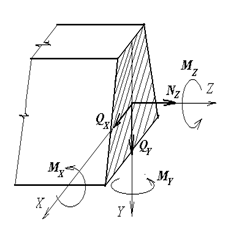
Рис. 2.1

Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):

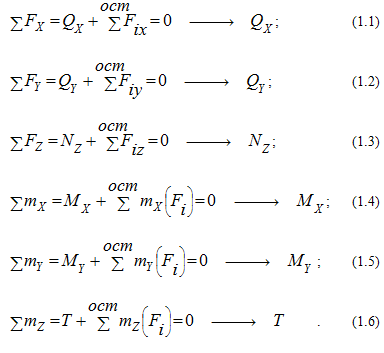
Уравнения равновесия системы сил

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия:R=0, M_o=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

∑x_i =0,      ∑M_ix=0;

∑y_{i =0},      ∑M_iy=0;                 (1.20)

∑z_i =0,      ∑M_iz=0.

При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

∑x_i =0;

∑M_o=0. (1.24)

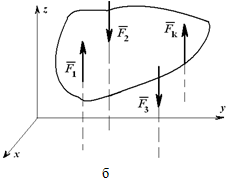
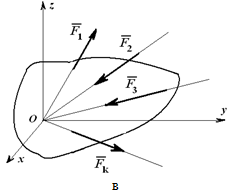
Рисунок 1.26

Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

∑z_i =0;

∑M_ix=0; (1.25)

∑M_iy=0.

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

∑x_i =0;

∑y_{i =0}; (1.26)

∑z_i =0

и два уравнения для плоской системы:

∑x_i =0;

∑y_{i =0}. (1.27)

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.