1. Исходные данные для выполнения лабораторной работы Лабораторная работа «Кинематический анализ механизма»

Схема кривошипно-ползунного механизма приведена на рис. 1. Точка С является центром масс шатуна и расположена посередине его длины, т.е. .

Требуется:

• построить траектории движения точек,,за один полный поворот кривошипа;

• определить скорости и ускорения заданных точек механизма;

• исследовать изменение скоростей и ускорений заданных точек механизма.

• Механизм обязательно имеет неподвижные1, 5,ведущее2 иведомые3, 4 звенья (рис. 1).

• 

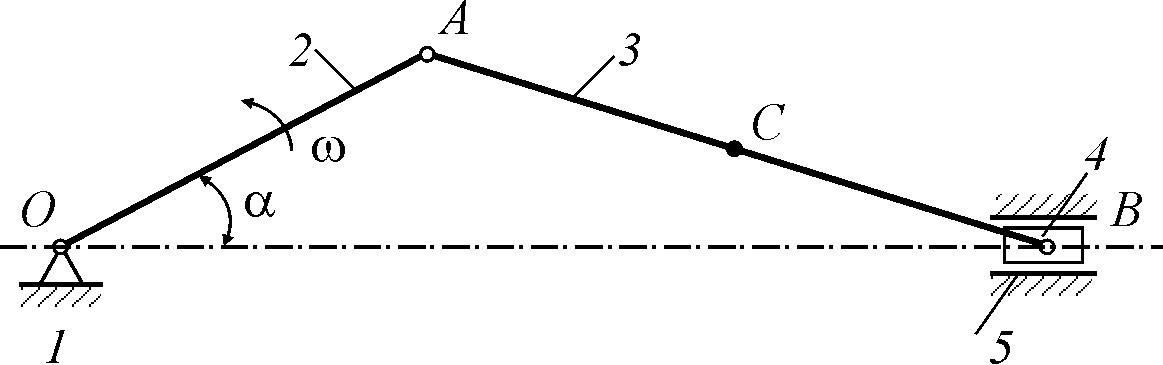
• Рис. 1.Кривошипно-ползунный механизм

Исходными данными являются:

 – угол поворота кривошипа в исходном положении, град;

–длина кривошипа, м;

–отношение длины кривошипа к длине шатуна;

 – угловая скорость вращения кривошипа, с^-1.

Исходные данные выбираются из табл. 1 в соответствии с учебным шифром, которым является набор из трех последних цифр студенческого билета (зачетной книжки). Например, для студенческого билета № 22041/06, учебный шифр – число 041, где цифры 0, 4 и 1 составляют соответственно первую, вторую и третью цифру учебного шифра. Для рассматриваемого учебного шифра исходными данными для выполнения лабораторной работы будут являться следующие величины:

; м;;с^-1.

Таблица 1.

Первая цифра шифра	, град	Вторая цифра шифра	, м	Третья цифра шифра		, с-1
0	30	0	0,08	0	0,27	30
1	45	1	0,10	1	0,31	35
2	60	2	0,16	2	0,34	40
3	120	3	0,18	3	0,26	45
4	150	4	0,13	4	0,32	50
5	135	5	0,15	5	0,40	55
6	210	6	0,20	6	0,35	25
7	225	7	0,12	7	0,30	20
8	240	8	0,22	8	0,25	15
9	300	9	0,24	9	0,28	10

2. Методические указания к выполнению лабораторной работы

2.1. Построение траектории движения точек за один полный поворот кривошипа

На листе миллиметровой бумаги формата А4 в масштабе строится механизм в заданном положении (рис. 2), а затем в 8 или 12 положениях ведущего звена в зависимости от исходных данных.

Если заданный угол кратен, то строитсяположений точки(через каждые). Если заданный угол кратен, то строитсяположений точки(через каждые).

Поскольку длина шатуна величина постоянная, а точка всегда перемещается по горизонтальной оси, то для каждого положения точки графическим путем определяется соответствующее положение точки .На рис. 2 показано построение первых двух положений механизма при заданном угле.

Приработе механизма траекторией точкибудет окружность радиуса, а траекторией движения точки– прямая, совпадающая с осью.

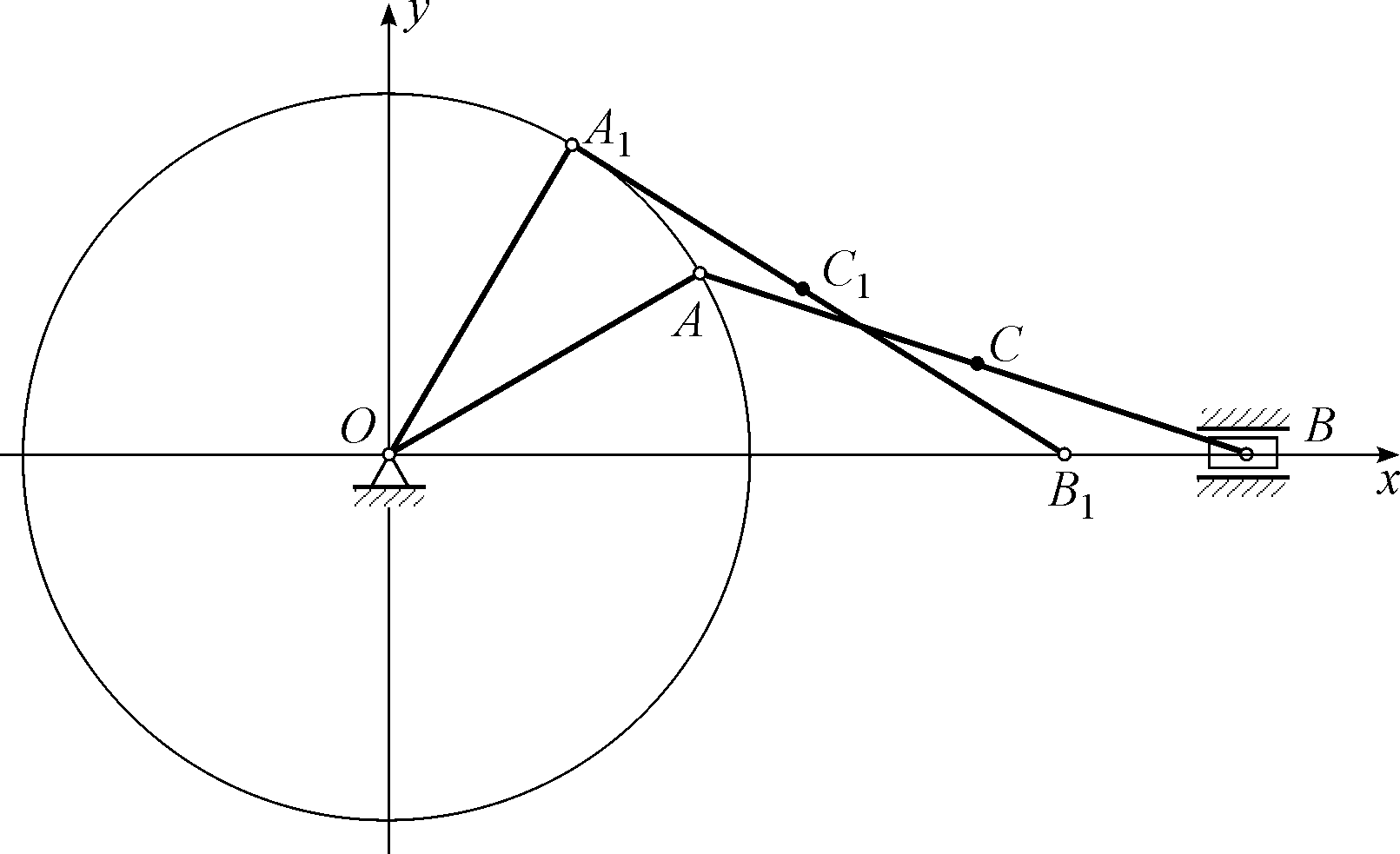
Рис. 2.Построение траектории точек,,за один полный поворот кривошипа

Поскольку точка находится по середине длины шатуна , то ее местоположение для каждого угла поворота кривошипа также определяется при графическом построении положения шатуна. Получившиеся соответственно 12 или 8 точек соединяют плавной кривой и устанавливают траекторию движения точкиза один полный оборот кривошипа. Получающаяся замкнутая кривая должна иметь вид эллипса. Уравнение эллипса:

, (1)

где ,– полуоси эллипса (рис. 3).

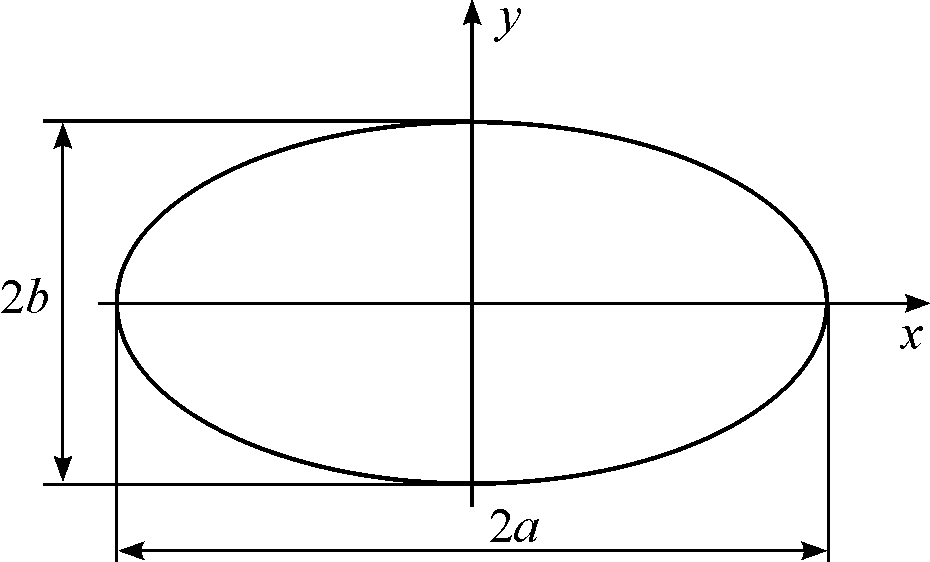
Рис. 3.К определению траектории движения точки

Измеряя получившиеся полуоси эллипса в масштабе, принятом для построения траектории, определяют величины ,и записывают уравнение движения точки.

Построив траектории движения точек ,,за один полный оборот кривошипа следует заполнить соответствующие столбцы табл. 2:,.

Таблица 2.

Точка	, град	, м	, м		, м	, м