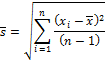Лабораторная работа №1

ОСНОВЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ

ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

I. ЦЕЛЬ РАБОТЫ

Ознакомиться с методами статистической обработки результатов испытания или обследования строительных конструкций.

ЗАДАЧИ:

1. Освоить процедуру нахождения закона распределения случайной величины;

2. Освоить процедуру построения парной зависимости по экспериментальным данным;

3. Научиться производить оценку статистической значимости полученных зависимостей и распределений.

II. ОБЩИЕ СВЕДЕНИЯ

1. Одномерные случайные величины.

При обследовании и испытании строительных конструкций, проведении других экспериментальных работ исследователю постоянно приходится сталкиваться с величинами, значения которых имеют случайный характер. Случайными величинами являются геометрические размеры конструкций, механические характеристики материалов, значения нагрузок и воздействий на конструкции и сооружения и др.

Случайные величины характеризуются некоторым разбросом значений, обусловленным различными факторами, учесть которые в эксперименте не представляется возможным (или необходимым) ввиду сложного характера влияния их на исследуемую величину. Чтобы иметь возможность оперировать изучаемой случайной величиной в расчетах, необходимо произвести математическую обработку результатов испытания или наблюдений.

Обработка экспериментальных данных производится методами математической статистики. Она включает в себя вычисление характеристики эмпирического распределения, отсев грубых погрешностей, определение закона распределения случайной величины и оценку достоверности принятого распределения.

Результатом исследования какой-либо случайной величины является ограниченный ряд значений , , … , , которые она принимает в ходе наблюдений – выборка. Основными характеристиками (выборочными оценками) эмпирического распределения являются:

а) выборочное среднее

(1)

представляющее собой среднее значение выборки;

б) выборочное среднеквадратическое отклонение

(2)

характеризующее плотность распределения случайных значений вокруг математического ожидания;

в) коэффициент вариации

(3)

являющийся мерой относительной изменчивости наблюдаемой случайной величины.

При выборках небольшого объема () исключение грубых погрешностей, появившихся либо из-за серьезной ошибки в ходе измерений или расчетов, либо в результате весьма редкого сочетания факторов, влияющих на результат эксперимента, производится методом вычисления максимального относительного отклонения:

(4)

где – крайний (наибольший или наименьший) элемент выборки;

– табличное значение статистики , вычисленное при доверительной вероятности (табл. 1).

Проверка осуществляется, как правило, при уровне значимости (доверительная вероятность ). Если неравенство не выполняется, то проверяемый элемент исключается, после чего характеристики распределения вычисляются для сокращенной выборки. Процедура повторяется до тех пор, пока не будет удовлетворено неравенство (4).

Для того чтобы графически представить эмпирическое распределение, выборка разбивается на равные интервалы. Количество интервалов принимается обычно в пределах 10-20. При слишком большом числе интервалов (больше 20) ощущается влияние даже небольших случайных колебаний. Если число интервалов меньше 10, то построение теоретической кривой по эмпирическим данным может быть затруднено /16. С.26/. Подсчитывается частота попадания случайных значений в каждый из интервалов. По результатам вычислений строится гистограмма.

Следующим этапом статистической обработки данных является определение закона распределения случайной величины. Существует большое количество теоретических распределений, некоторые из них представлены в таблице 2. График распределения представляет собой кривую или ломаную линию, называемую плотностью распределения вероятностей. Площадь фигуры, образуемой линией распределения, осью абсцисс и двумя вертикальными линиями и , представляет собой значение вероятности попадания случайной величины в интервал (A, B). Определение закона распределения осуществляется в следующем порядке:

а) принимается гипотеза о том или ином виде распределения;

б) вычисляется параметры проверяемого распределения;

в) проверяется неравенство

(5)

где – объем выборки;

- количество значений выборки, попадающее в -й интервал;

- теоретическая вероятность попадания случайной величины в -й интервал, ;

- значение функции распределения в центре интервала;

- величина интервала;

- табличное значение хи-квадрат критерия (табл. 3)

- количество интервалов в гистограмме;

– число параметров распределения;

- уровень значимости.

Шаг интервала: , (6)

где (7)

При этом необходимо выполнение условия /16. С.293/. Если в некоторых интервалах это условие не выполняется, то они объединяются с соседними. В случае выполнения неравенства (5) при уровне значимости гипотеза о теоретическом законе распределения принимается, в других случаях – отвергается. Чем меньше величина , тем лучше соответствует принятый теоретический закон эмпирическому распределению.

Таблица 1

Квантили распределения максимального относительного отклонения

n	Уровень значимости			n	Уровень значимости			n	Уровень значимости
	0,10	0,05	0,01		0,10	0,05	0,01		0,10	0,05	0,01
5	1,79	1,87	1,96	12	2,23	2,39	2,66	19	2,43	2,60	2,93
6	1,89	2,00	2,13	13	2,26	2,43	2,71	20	2,45	2,62	2,96
7	1,97	2,09	2,27	14	2,30	2,46	2,76	21	2,47	2,64	2,98
8	2,04	2,17	2,37	15	2,33	2,49	2,80	22	2,49	2,66	3,01
9	2,10	2,24	2,46	16	2,35	2,52	2,84	23	2,50	2,68	3,03
10	2,15	2,29	2,54	17	2,38	2,55	2,87	24	2,52	2,70	3,06
11	2,19	2,34	2,61	18	2,40	2,58	2,90	25	2,54	2,72	3,07

Таблица 2

Законы распределения случайных величин

№№ п/п	Распределение		Формула	Параметры распределения
1	Нормальное (Гаусса)
2	Лапласа
3	Рэлея
4	Показатель-ное
5	Равномерное

Таблица 3

Квантили хи-квадрат распределения

	Уровень значимости α				Уровень значимости α
	0,10	0,05	0,01		0,10	0,05	0,01
1	2,706	3,841	6,635	6	10,645	12,592	16,812
2	4,605	5,991	9,210	7	12,017	14,067	18,475
3	6,251	7,815	11,345	8	13,362	15,507	20,990
4	7,779	9,488	13,277	9	14,684	16,919	21,666
5	9,236	11,070	15,086	10	15,987	18,307	23,209

Пример 1. Нахождение и проверки закона распределения стрелки искривления () стержней решетки стропильных ферм.

Таблица 4
Выборка
№№ п/п
1	3,2	75,69
2 3	4,4 5,6	56,25 39,69
4 5 6	6,1 6,9 7,5	33,64 25,00 19,36
7 8	8,3 9,2	12,96 7,29
9 10 11 12	10,3 10,8 11,6 11,7	2,56 1,21 0,09 0,04
13 14 15 16 17	12,1 12,4 13,0 13,5 13,9	0,04 0,25 1,21 2,56 4,00
18 19 20	14,4 14,8 15,6	6,230 8,41 13,69
21 22	16,7 17,2	23,04 28,09
23 24 25	18,4 19,4 20,7	42,25 56,25 77,44
	297,6	537,26

Выборочные оценки:

- математическое ожидание (1)

- среднеквадратическое отклонение (2)

Проверка совместимости данных (4):

(табл. 1)

Грубых ошибок нет.

Выборка разбивается на десять интервалов с шагом . Поочередно проверяются гипотезы о возможности описания выборки законами распределения (5):

а) Гаусса

б) Лапласа

15

Сравнение характеристик со значениями, приведенными в табл. 3, показывает, что данная выборка может быть удовлетворительно описана обоими законами распределения. Однако, распределение Гаусса дает меньшее значение и, следовательно, точнее описывает приведенную выборку. Таким образом, приведенная выборка подчиняется нормальному закону.

Таблица 5

Вычисление характеристики

№	середина интервала		Распределение Гаусса				Распределение Лапласа
1 2 3 4 5 6 7 8 9 10	3 5 7 9 11 13 15 17 19 21	1 2 3 2 4 5 3 2 2 1	0,0144 0,0291 0,0493 0,0699 0,0828 0,0821 0,0680 0,0472 0,0274 0,0133	0,029 0,058 0,099 0,140 0,166 0,164 0,136 0,094 0,056 0,027	0,73 1,45 2,48 3,50 4,15 4,10 3,40 2,35 1,38 0,68	0,308 0,109 0,643 0,005 0,198 0,047 0,052 0,429	0,0105 0,0190 0,0346 0,0628 0,1142 0,1076 0,0592 0,0325 0,0179 0,0098	0,021 0,038 0,069 0,126 0,228 0,215 0,118 0,065 0,036 0,020	0,53 0,95 1,73 3,15 5,70 5,38 2,95 1,63 0,90 0,50	2,425 0,420 0,507 0,027 0,001 1,981
		25		0,968	24,22	1,791		0,936	23,42	4,661

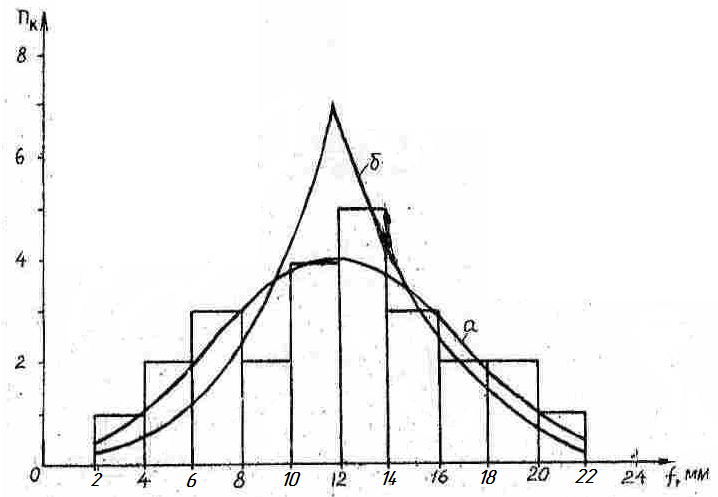
Рис. 1. Гистограмма и теоретические распределения:

а – Гаусса (нормальное), б – Лапласа

распределения с параметрами ,

Таблица 11

Исходные данные (время эксплуатации конструкций t и скорость коррозии v)

t год
	1	2	3	4	5	6	7	8	9	10
7	18	64	24	4	58	74	3	14	22	47
19	53	34	53	21	25	34	27	48	55	12
13	36	52	37	6	46	55	17	34	36	33
25	74	17	75	27	17	25	37	50	63	4
16	47	43	38	13	28	52	20	39	42	25
22	69	41	53	24	23	36	33	49	53	9
7	5	82	17	1	74	77	2	7	3	67
19	62	22	44	16	30	47	28	47	47	11
10	22	57	32	8	44	65	5	82	27	42
16	54	47	41	15	26	48	19	46	38	16
28	89	4	84	46	6	14	55	77	75	2
13	42	47	35	9	35	54	15	44	41	28
25	86	6	64	33	12	16	38	67	66	3
22	58	38	49	17	29	29	28	56	46	14
7	13	66	7	5	57	64	7	25	33	55
16	31	44	43	12	33	43	16	42	44	23
19	44	32	47	20	31	45	25	48	51	19
28	84	25	66	49	15	20	43	57	59	5
10	25	58	21	2	50	59	11	35	38	39
25	67	13	58	38	19	31	35	54	54	8
7	7	73	13	3	66	66	8	22	17	58
28	76	35	60	51	10	23	48	63	58	7
22	56	27	62	23	14	33	30	53	50	10
13	29	51	40	19	36	57	14	41	37	27
10	16	50	26	7	38	61	13	38	24	36