10,4 М/с.

Таким образом, значение коэффициента динамической нагрузки К_д=1,5 было принято правильно.

Пример 2

Рассчитать коническую эвольвентную прямозубую передачу по примеру (рис. 71). Согласно выше приведенных расчетов механизма получаем исходные данные: передаваемая мощность N=12,5 кВт; угловая скорость конического колеса соответствует скорости звездочки, т. е. рад/с; передаточное числоu=3,15; следовательно, получаем рад/с.

Решение

Поскольку передача открытая, то проектный расчет проводим по напряжениям изгиба (определяем средний модуль зацепления m_c), а проверочный расчет – на контактную прочность (для закрытой передачи порядок расчета обратный).

Материал и термообработку для зубчатых колес назначаем те же, как и в примере 1. Поэтому допускаемые напряжения для зубьев примем: на изгибную прочность [] = 146 МПа и на контактную прочность [] = 800 МПа. Учитывая, что передача тихоходная и открытая, то возьмем зубчатые колеса 8 степени точности.

Проектный расчет на изгиб проводим по формуле

,

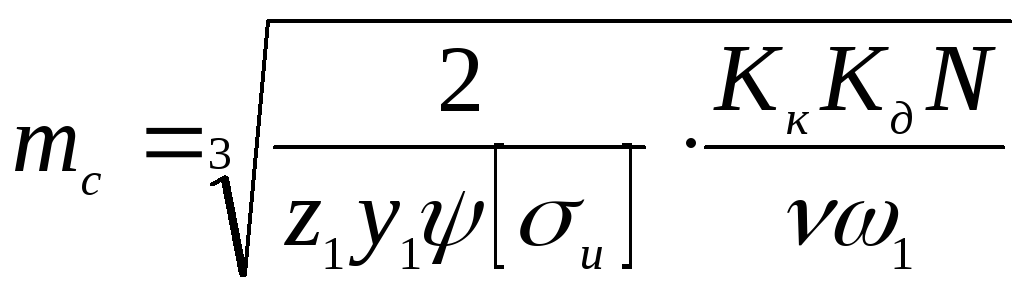где – коэффициент ширины венца конических зубчатых колес по среднему модулю, рекомендуется его значения брать в пределах, принимаем;– коэффициент снижения нагрузочной способности прямых зубьев конических передач, по рекомендациям;z₁ – число зубьев шестерни, принимаем z₁=20; y₁ – коэффициент формы зуба (прил. Е), для z₁=20 принимаем ; коэффициентыК_к и К_д устанавливаются по аналогии с примером 1. С учетом принятых значений средний модуль конической передачи равен

м =6,9 мм.

Вычисляем углы наклона образующих делительного конуса шестерни и колеса

,

Следовательно, и.

Ширина венца зубчатых колес мм.

Торцевой модуль определим как

мм.

Согласно ГОСТа (прил. Д) принимаем модуль m=8 мм.

Проверочный расчет прямых зубьев конических колес передач с углом пересечения осей, равным 90⁰ проводим по по следующей формуле:

,

где мм. Тогда

Па =

=87 МПа < МПа.

Контактная прочность обеспечена.

Для определения геометрических размеров зубчатых колес принимаем коэффициент высоты головок зубьев и коэффициент радиального зазора зубьев.

Высота головок зубьев

мм.

Высота ножек зубьев

мм.

Полная высота зубьев

мм.

Для каждого зубчатого колеса определяем делительный диаметр d, диаметр вершин d_а, диаметр впадин d_f:

для шестерни

мм,

мм,

мм,

для колеса

мм,

мм,

мм.

Окружная скорость передачи

м/с.

Следовательно, значения коэффициента динамической нагрузки К_д=1,3 было принято правильно.

Задача Д4

Вариант 1

По данным задачи 3 (см. рис. 61) рассчитать ведомый тихоходный вал зубчатого редуктора и подобрать для него подшипники качения. Недостающие данные принять конструктивно. Дать рабочий эскиз вала.

Вариант 2

По данным задачи 3 (см. рис. 61) рассчитать быстроходный вал трех­ступенчатого цилиндрического редуктора и подобрать для него под­шипники качения. Недостающие данные принять конструктивно. Дать рабочий эскиз вала.

Вариант 3

По данным задачи 3 (см. рис. 63) рассчитать быстроходный вал ре­дуктора и подобрать для него подшипники качения. Недостающие данные принять конструктивно, считая ориентировочно расстояние между подшипниками вала шестерни l=2b, где b – ширина шестерни. Дать рабочий эс­киз вала.

Вариант 4

По данным задачи 3 (см. рис. 64) рассчитать выходной тихоходный вал редуктора с одним зубчатым колесом и подобрать к нему подшипники качения. Недоста­ющие данные принять конструктивно. Дать рабочий эскиз вала.

Вариант 5

По данным задачи 3 (см. рис. 65) рассчитать вал тихоходной ци­линдрической ступени соосного двухступенчатого редуктора и подо­брать для него подшипники качения. Недостающие данные принять конструктивно. Дать рабочий эскиз вала.

Вариант 6

По данным задачи 3 (см. рис. 66) рассчитать быстроходный вал от­крытой конической зубчатой передачи и подобрать для него подшипники качения. Недостающие данные принять конструктивно, считая ориентировочно расстояние между подшипниками l=5d, где d – ди­аметр вала, определяемый по крутящему моменту, Дать рабочий эс­киз вала.

Вариант 7

По данным задачи 3 (см. рис. 67) рассчитать быстроходный вал ре­дуктора и подобрать для него подшипники качения. Недостающие данные принять конструктивно, считая ориентировочно расстояние между подшипниками вала конической шестерни l=5d, где d – ди­аметр вала, определяемый по крутящему моменту. Дать рабочий эс­киз вала.

Вариант 8

По данным задачи 3 (см. рис. 68) рассчитать быстроходный вал ци­линдрической зубчатой передачи и подобрать для него подшипники качения. Принять силу натяжение ремней 0,1F. Недостающие данные взять конструктивно. Дать рабо­чий эскиз вала.

Вариант 9

По данным задачи 3 (см. рис. 69) рассчитать быстроходный вал ре­дуктора и подобрать для него подшипники качения. Недостающие данные принять конструктивно, считая ориентировочно расстояние между подшипниками l=5d, где d – диаметр вала, определяемый по крутящему моменту. Дать рабочий эскиз вал

Вариант 10

По данным задачи 3 (см. рис. 70) рассчитать быстроходный вал ци­линдрической передачи редуктора и подобрать для него подшипники качения. Недостающие данные принять конструктивно. Дать рабо­чий эскиз вала.