3.6. Примеры решения задач д3
Пример 1
Приводная станция подвесного конвейера (рис. 71) состоит из электродвигателя 1, муфт 2 и 4, двухступенчатого редуктора 3, цилиндрической и конической зубчатых передач 5, 6 и звездочки для тяговой цепи 7. Подобрать электродвигатель, разбить общее передаточное число привода по ступеням и рассчитать быстроходную зубчатую передачу редуктора при условии, что окружное усилие на звездочке Ft=25 кН, скорость цепи V=0,5 м/c, шаг цепи t=32 мм, число зубьев звездочки z=20.
Рис. 71
Решение
Определяем полезную мощность Nп приводной станции, используя исходные данные
кВт.
Общий коэффициент полезного действия (к.п.д.) данного механизма составит
,
где
– к.п.д. цепной передачи;
– конической передачи;
– открытой зубчатой передачи;
– зубчатой передачи редуктора;
– к.п.д. одной пары подшипников качения.
С учетом числовых значений (табл 1, прил.
В) получаем
.
Используя полученные значения, определяем мощность электродвигателя, которая должна быть не менее
кВт.
Назначаем
асинхронный электродвигатель АО72-2
(прил. Г) мощностью Nэ
=
20 кВт с частотой вращения nэ=2940
об/мин или с угловой скоростью
рад/с.
Угловая
скорость звездочки
с радиусом
мм
составит
рад/с, и тогда получим общее передаточное
число привода
.
Это число разбиваем по ступеням механизма, учитывая рекомендации (табл. 2, прил. Д)
,
где u1, u2, u3, u4 – соответственно передаточные числа быстроходной и тихоходной ступени редуктора, открытой цилиндрической и конической передачи. Фактическое передаточное число (u=63) отличается от номинального (u=62,67) не более чем на 0,5 %, что вполне допустимо.
Согласно
условию примера рассчитываем быстроходную
зубчатую передачу редуктора. Исходные
данные для этого расчета: мощность,
передаваемая шестерней N1=Nэ=18,38
кВт; угловая скорость шестерни
рад/с; передаточное числоu1=2.
Учитывая,
что передаточное число незначительное,
материал для обоих зубчатых колес
назначаем одинаковый – сталь 45 с закалкой
и отпуском в масле. Механические свойства
этой стали (прил. А): предел прочности
МПа, предел текучести
МПа, твердостьHRC35
или НВ350.
Допускаемое контактное напряжение для зубьев колес (табл. 1, прил. Е) находим как
МПа.
Определяем
допускаемое напряжение для зубьев на
изгиб
с учетом коэффициента запаса прочности
и эффективного коэффициента концентрации
напряжений
у корня зуба (прил. Ж), предварительно
вычислив предел выносливости материала
зубьев как
=
,
приняв
МПа. Тогда при условии, что зубья работают
одной стороной, получаем
МПа.
Согласно
схеме пара зубчатых колес закрытая
(работает в масляной ванне), соответственно
проектный расчет проводим на контактную
прочность, определяя делительное
межосевое расстояние а
предачи. Исходные данные для расчета:
u=u1=
,
рад/с, следовательно,
рад/с;N=12,5
кВт или 12,5
Вт;
МПа или
Па.
Коэффициент
ширины венца зубчатых колес принимаем
.
Поскольку действующая на зубья нагрузка
постоянная и вал жесткий, то считаем,
что коэффициент концентрации нагрузки
равенКк=1.
Назначаем для передачи 7-ю степень
точности, и полагая, что окружная скорость
передачи V=12…18
м/с, в ссвязи с рекомендациями для
принятой твердости поверхности зуба
принимаем коэффициент динамической
нагрузки Кд=1,5.
При выборе коэффициентов использованы
рекомендации (табл. 1, 2, прил. Ж) .
Делительное межосевое расстояние определяем по формуле [1]
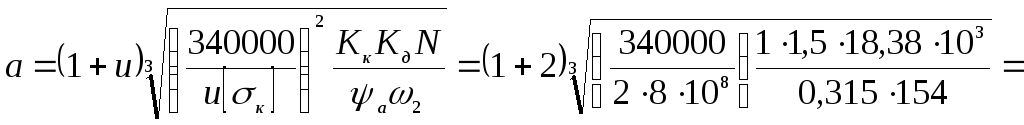
=0,086 м=86 мм.
Принимаем ближайшее большее значение по ГОСТ 16532-70, что соответствует а=100 мм.
Выбираем число зубьев шестерни z1, колеса z2 и модуль зацепления m, учитывая, что эти параметры в нормальных зубчатых передачах связаны зависимостью
.
Назначаем модуль зацепления m=2,5 мм, тогда при а=100 мм получаем (z1+z2)=80. Это число разбиваем, приняв z1=27, z2=53.
Тогда фактическое передаточное число
.
Отклонение
от заданного значения
%,
что по ГОСТу допустимо (см. прил. Д).
Проверим зубья на изгиб. Т.к. материал зубьев шестерни и колеса одинаковый, то этот расчет достаточно выполнить для зубьев шестерни. Ширина венца зубчатых колес
мм.
Коэффициент
формы зуба (табл.2, прил. Е)
.
Напряжение изгиба в зубьях шестерни определяем по формуле
Па = 92 МПа <
МПа.
Проведем
геометрический расчет передачи. В
соответствии с ГОСТ 13755-81 примем
коэффициент высоты головок зубьев
и коэффициент радиального зазора
.
Высота головок зубьев
мм.
Высота ножек зубьев
мм.
Полная высота зуба
мм.
Для каждого зубчатого колеса определяем делительный диаметр d, диаметр вершин – da, диаметр впадин – df:
для шестерни
мм,
мм,
мм;
для колеса
мм,
мм,
мм.
Окружная скорость передачи