2. Рассмотрим теперь матричную игру, платежная матрица которой является транспонированной к матрице задачи 1, т.Е. Игра задается матрицей

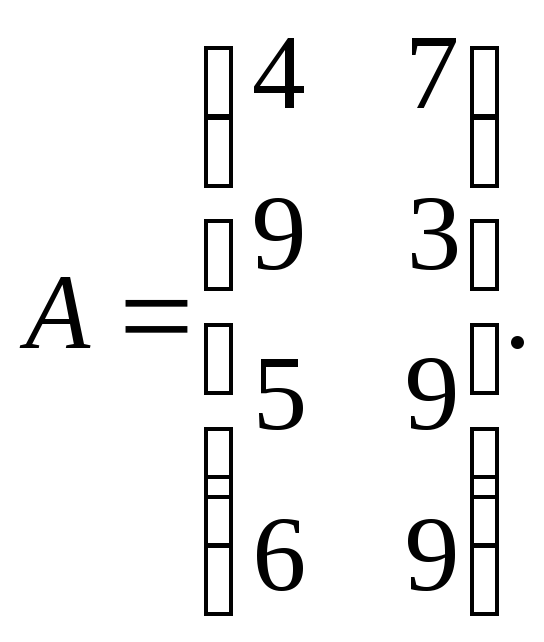
В новой игре первый игрок имеет четыре чистые стратегии, а второй − две. Нижняя цена игры а верхняя цена игры .

Так как , то у этой игры нет седловой точки, поэтому нужно искать ее решение в смешанных стратегиях. Пусть − вектор смешанных стратегий первого игрока, а − вектор смешанных стратегий второго игрока. Платежная функция данной игры равна:

Второй игрок имеет две чистые стратегии, поэтому графически будет решаться задача второго игрока. Построения выполняются аналогично п.1, если поменять местами первого и второго игроков (см. рисунок 1.4). Цель второго игрока, согласно его осторожному поведению, состоит в минимизации его возможного риска. Риск второго игрока (т.е. максимально возможный проигрыш второго игрока при применении им той или иной смешанной стратегии) на рисунке 1.4 показан жирной линией. Точка M обозначает минимальный риск второго игрока. Она лежит на пересечении отрезков, соответствующих второй и четвертой чистым стратегиям первого игрока.

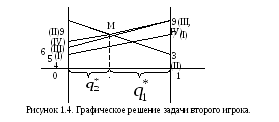
Обозначим оптимальную смешанную стратегию второго игрока . Для нахождения значений и воспользуемся утверждением 3. Активными стратегиями первого игрока являются вторая и четвертая. Тогда

1) , => .

2) , =>.

Приравняем эти значения к цене игры и добавим уравнение , получим систему уравнений:

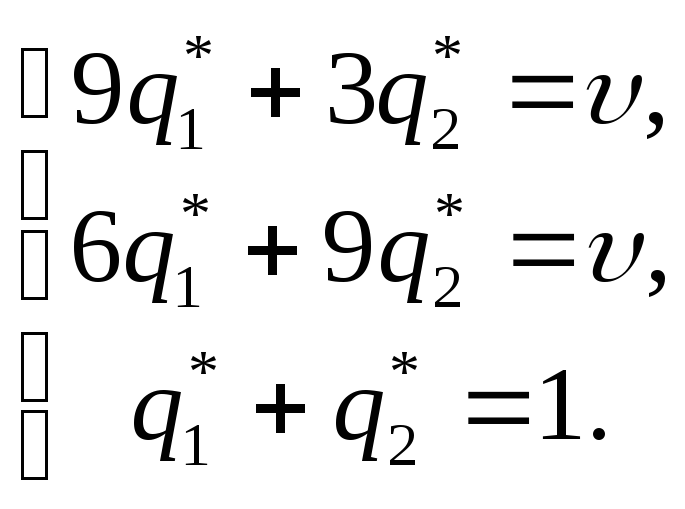Решив эту систему, получаем

Теперь найдем оптимальную смешанную стратегию первого игрока, . Так как его активные стратегии − вторая и четвертая, а первая и третья пассивные, то . Следовательно, . Применяя утверждение 1 и учитывая, что цена игры уже найдена, получим систему уравнений:

Решая эту систему, получаем

Итак, решение матричной игры задается векторами и ценой игры :

, .

Задача 2. Оптимальное распределение заказа между фирмами

Предприниматель должен принять решение о приобретении d единиц продук-ции, которую выпускают две фирмы. Известно, что если он закажет первой фирме х изделий, то ему придется заплатить ей

f₁(x) = a₀ + a₁x + a₂x² (руб.),

а при выполнении этого заказа второй фирмой его затраты составят

f₂(x) = b₀ + b₁x + b₂x² (руб.).

Нужно найти оптимальное распределение заказа между фирмами, при котором общие затраты будут минимальными, а также определить максимальный уровень затрат, соответствующий самому неудачному решению предпринимателя.

Исходные значения параметров представлены в таблице:

d	a0	a1	a2	b0	b1	b2
100	25	2	0.2	15	6	0.3

Требуется:

1)  составить математическую модель оптимального распределения заказа между фирмами;

2)  найти графическим методом распределения заказа с минимальными и макси-мальными затратами;

3)  определить оптимальное распределение заказа методом множителей Лагранжа; дать экономическую интерпретацию множителю Лагранжа.

Решение.

1. Построение математической модели

В данной задаче следует определить

х₁ — число изделий, заказанное первой фирме;

х₂ — число изделий, заказанное второй фирме.

Эти величины являются переменными модели. Ясно, что они должны принимать неотрицательные значения, т.е. х₁ ≥ 0 и х₂ ≥ 0; причем их сумма должна равняться общему числу заказанных изделий, т.е. х₁ + х₂ = 100.

Цель предпринимателя — минимизировать суммарные затраты на выполнение заказа. Так как стоимость х₁ изделий, заказанных первой фирме составляет

f₁(x₁) = 25 + 2 x₁+ 0.2,

а стоимость х₂ изделий, заказанных второй фирме, составляет

f₂(x₂) = 15 + 6 x₂+ 0.3,

то суммарные затраты Z на выполнение всего заказа равны

Z = f(x₁, x₂) = f₁(x₁) + f₂(x₂) = 25 + 2 x₁+ 0.2 + 15 + 6 x₂+ 0.3 (руб.).

Таким образом, целевая функция (ЦФ) имеет вид:

f(x₁, x₂) = 40 + 2 x₁+ 0.2 + 6 x₂+ 0.3.

Математическая модель задачи может быть записана в таком виде: найти неизвестные значения переменных х₁ и х₂, доставляющие минимальное значение ЦФ

Z = 40 + 2 x₁ + 0.2 + 6 x₂ + 0.3 → min (1)

и удовлетворяющие ограничениям

х₁ + х₂ = 100, (2)

х₁ ≥ 0, х₂ ≥ 0. (3)

2. Нахождение графическим методом распределений заказа с минимально и максимально возможными уровнями затрат.

а) Построение ОДР

ОДР состоит из точек плоскости с неотрицательными координатами, которые лежат на прямой, задаваемой уравнением (2). Следовательно, ОДР представляет собой отрезок прямой АВ (см. рис. 1).

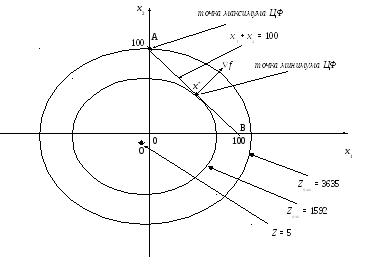
Рис. 1. Графическое решение задачи 1

б) Построение и анализ линий уровня ЦФ

Приведем ЦФ к более удобному для анализа виду, выделив полные квадраты по каждой ее переменной:

f(х₁, х₂) = 40 + 2 x₁ + 0.2 + 6 x₂ + 0.3 =

0.2( + 10x₁ + 25) + 0.3( + 20 x₂ + 100) + 5 = 0.2(х₁ + 5)² + 0.3(x₂ + 10)² + 5.

Пусть С — некоторое фиксированное число. Тогда линия уровня функции

f(х₁, х₂) = С

состоит из всех точек х = (х₁, х₂) плоскости, координаты которых удовлетворяют уравнению

0.2(х₁ + 5)² + 0.3(x₂ + 10)² + 5 = С

или 0.2(х₁ + 5)² + 0.3(x₂ + 10)² = С – 5. (4)

Так как левая часть этого уравнения неотрицательна при любых значениях х₁ и х₂, то ясно, что должно выполняться неравенство С ≥ 5, поскольку при С < 5 это уравнение не имеет решений.

Если С = 5, то линия уровня целевой функции содержит единственную точку О = (-5, -10), так как левая часть уравнения (4) равна нулю лишь при х₁ = -5 и х₂ = ‑10.

При С > 5 линии уровня являются эллипсами¹ с общим центром в точке О, размеры которых увеличиваются с ростом параметра С (см. рис. 1).

в) Нахождение точки минимума ЦФ

С ростом параметра С линии уровня ЦФ становятся все ближе к ОДР задачи — отрезку АВ. Сначала они не имеют с ним общих точек, но при определенном значении С = С_min линия уровня коснется этого отрезка в некоторой точке х^* = (). Эта точка соответствует наименьшему значению С, при котором линия уровня имеет общие точки с АВ. Значит, точка х^* является решением задачи, так как в ней ЦФ достигает минимума на этом отрезке.

Для определения ее координат воспользуемся следующим фактом. Если прямая

х₁ + х₂ = 100,

касается в некоторой точке линии уровня ЦФ, задаваемой уравнением

f(х₁, х₂) = С,

то градиент f = , вычисленный в точке касания, перпендикулярен этой прямой. Это означает, что координаты ее вектора нормали прямой, т.е. вектора а = (1, 1), пропорциональны координатам вектора f. Таким образом, выполняется соотношение

или .

Поскольку = 0.4х₁ + 2, а = 0.6х₂ + 6, то из равенства частных производных получаем, что координаты точки касания удовлетворяют уравнению

.

Значит, точку минимума ЦФ можно найти, решив систему уравнений

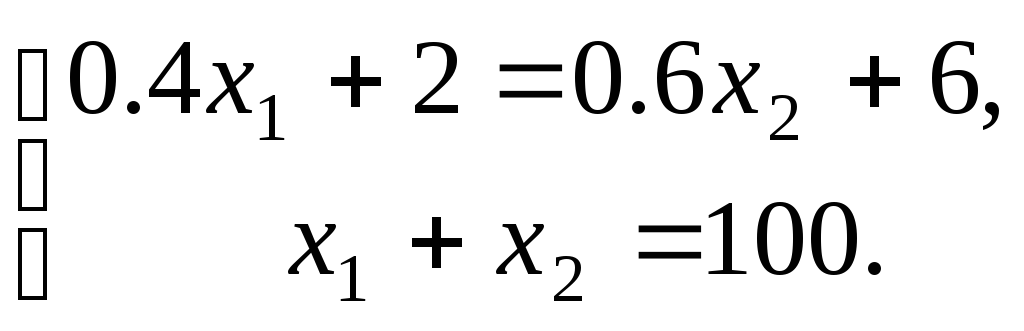
или (5)

Ее решение: = 64, = 36. Вычислим значение ЦФ в этой точке:

Z^* = f() = 0.2(64 + 5)² + 0.3(36 + 10)² + 5 = 1592 (руб.).

Итак, получено решение задачи (1) – (3): предприниматель должен заказать первой фирме 62 изделия, а второй фирме — 36 изделий. В этом случае его затраты будут минимальными и составят 1592 руб.

г) Нахождение точки максимума ЦФ

При дальнейшем увеличении параметра С линии уровня будут пересекать ОДР в точках, которым соответствуют все возрастающие значения ЦФ. Поэтому последняя точка пересечения является точкой максимума ЦФ на отрезке АВ. Из рис. 1 видно, что в нашей задаче ЦФ достигает максимума в точке А = (0, 100). В этой точке значение ЦФ равно

Z_max = f(0, 100) = 0.2(0 + 5)² + 0.3(100 + 10)² + 5 = 3635 (руб.).

Таким образом, самым неудачным решением предпринимателя будет выбор второй фирмы в качестве единственного исполнителя заказа. В этом случае его затраты будут максимальными и составят 3635 руб.

Замечание. Графический анализ показывает, что ЦФ достигает своего максимума в одной из крайних точек отрезка АВ. Поэтому для определения точки максимума проще всего сравнить значения ЦФ в точках А и В. Та точка, в которой это значение больше, будет искомой. Если же значения ЦФ в этих точках равны, то это означает, что обе они являются точками максимума.