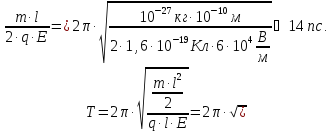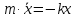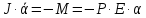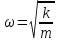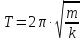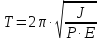- •Кафедра медицинской и биологической физики
- •Рекомендации к работе с пособием.
- •Приведём пример оформления решения задачи.
- •3. Колебания и волны, биоакустика
- •3.17. Гармонические колебания материальной точки массой 2 г происходят по закону:
- •4.28. Электронная поляризация в диэлектриках ..... От температуры.
- •4.45. Приведите примеры магнетиков, входящих в состав биологических систем.
- •4.46. Укажите тип магнетиков, к которому относятся свободные радикалы в биологических системах.
- •3.24. Уравнение затухающих колебаний в каноническом виде:
- •Для, учитывая, что при колебаниях, получаем, что соответствует максимуму знаменателя формулы:Значит, приговорить о резонансе не приходится.
- •3.27. В задаче 3.26 была найдена резонансная частота:
- •3.31. Ответ: 1) - в сторону уменьшения координаты х.
- •3.45. Интенсивность – это средняя по времени энергия, которую переносит волна через единичную площадку, ориентированную перпендикулярно направлению распространения волны.
- •3.46. Тепловая энергия, которая должна быть поглощена водой для того, чтобы вода нагрелась от начальной температуры до температуры кипения при нормальных условиях:
- •4.32. Решение. Речь идёт о дисперсии (зависимости от частоты переменного электрического поля) диэлектрической проницаемости биологических тканей. Общий ход такой зависимости представлен на рисунке
- •4.41. Решение. 1) Действующий фактор – электрический ток частотой 5 мГц, который является квазистационарным для электрических цепей длиной до
- •4.42. Решение. Выделим в объёме проводника малую область в виде цилиндра с площадью δs и высотой V:
- •4.51. Решение. Элемент работы при повороте объекта с магнитным моментом получим, если учтём, что и момент сил поля противоположны по знаку.
- •4.54. Решение. При параллельно соединённых элементах напряжение на каждом из элементов схемы одинаковое.
- •4.56. Решение. Для ответа на поставленный вопрос необходимо располагать данными о дисперсии импеданса живых и отмирающих биологических тканей. Эти данные представлены на рисунке.
- •4.65. Решение. При параллельно соединённых элементах напряжение на каждом из элементов схемы одинаковое.
- •Справочные материалы Фундаментальные постоянные
- •Наименования и обозначения приставок си для образования десятичных кратных и дольных единиц и их множители
- •Правила приближённых вычислений.
3.45. Интенсивность – это средняя по времени энергия, которую переносит волна через единичную площадку, ориентированную перпендикулярно направлению распространения волны.
Считая источник ультразвука точечным, изобразим схематически конус излучения:
I
– интенсивность, 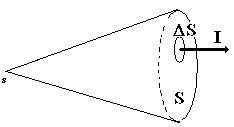
S – площадь поперечного сечения конуса излучения,
ΔS -единичная площадка,
s – источник излучения.
Пренебрегая
поглощением, запишем формулу для
интенсивности ультразвуковой волны:
![]() гдеP-
мощность излучателя.
гдеP-
мощность излучателя.
Далее,
воспользуемся модулем вектора Умова:
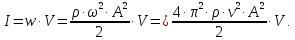 В
формуле для модуля вектора Умова (формуле
интенсивности волны):
В
формуле для модуля вектора Умова (формуле
интенсивности волны):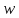 - объёмная плотность энергии,
- объёмная плотность энергии,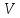 - скорость распространения звуковой
волны,
- скорость распространения звуковой
волны,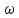 - круговая частота колебаний в звуковой
волне,
- круговая частота колебаний в звуковой
волне,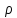 - плотность среды, в которой распространяется
волна,
- плотность среды, в которой распространяется
волна,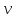 - частота колебаний,
- частота колебаний, -амплитуда смещения в звуковой волне.
Получим расчётную формулу из соотношения:
-амплитуда смещения в звуковой волне.
Получим расчётную формулу из соотношения: .
.
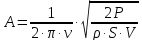 .
Подставим числовые значения в расчётную
формулу. Получим окончательный ответ:
.
Подставим числовые значения в расчётную
формулу. Получим окончательный ответ:
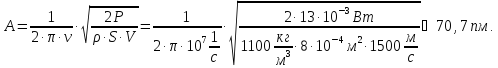
3.46. Тепловая энергия, которая должна быть поглощена водой для того, чтобы вода нагрелась от начальной температуры до температуры кипения при нормальных условиях:
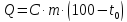 .
С другой стороны, эту энергию должна
принести поглощаемая водой звуковая
волна:
.
С другой стороны, эту энергию должна
принести поглощаемая водой звуковая
волна:
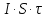 ,
где
,
где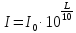 .
.
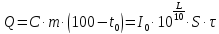 .
.
Откуда
получаем расчётную формулу для времени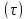 :
:
 .
.
Подставим
числовые значения в расчётную формулу.
Получим окончательный ответ:
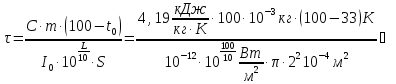
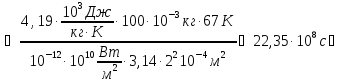
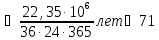 год.
год.
3.47.
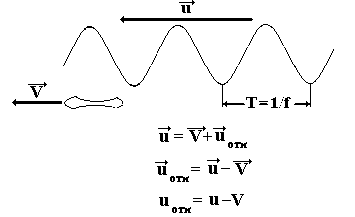
Частота «воспринимаемая» удаляющимся эритроцитом f':.
 .
.
Частота, приходящая на зонд от удаляющегося эритроцита:
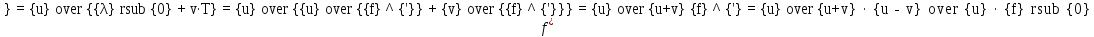 .
.
Выведем расчётную формулу, получим числовой ответ.
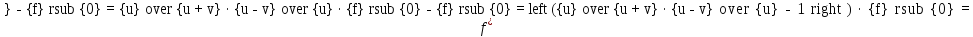
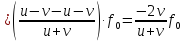 .
.
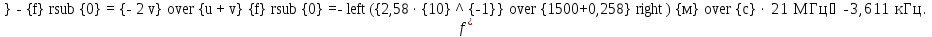
3.48.
Вспомним соотношение, связывающее длину
волны, скорость распространения волны
и частоту колебаний в волне:
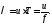 Для определения относительной скорости
волны используем правило сложения
скоростей классической механики:
Для определения относительной скорости
волны используем правило сложения
скоростей классической механики: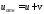
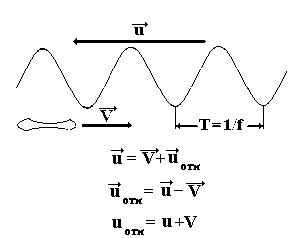
Определим
частоту ультразвука, которую «воспринимает»
эритроцит:
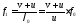
Определим частоту, отражённую движущимся эритроцитом:
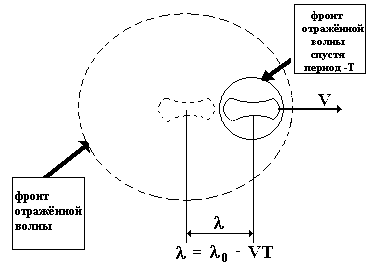
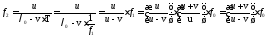
Выведем расчётную формулу, получим числовой ответ.
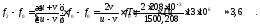
3.49. Угол α не может быть сделан меньше некоторого критического угла αкр из-за различия значений скорости распространения ультразвука в крови и в тканях стенки сосуда.

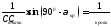

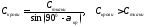

Ответ.
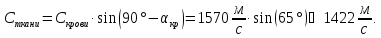
3.50. В национальном стандарте США в качестве одного из требований по безопасности при УЗИ вводится
тепловой
индекс:
 .
.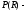 акустическая
мощность на глубинеR,
которую создаёт датчик,
акустическая
мощность на глубинеR,
которую создаёт датчик,
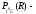 акустическая
мощность на глубинеR,
которая вызывает локальное повышение
температуры в тканях на
акустическая
мощность на глубинеR,
которая вызывает локальное повышение
температуры в тканях на
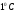 .
Используя условия задачи:
.
Используя условия задачи: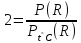 ,
,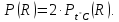
Ответ.
Зонд прибора создаёт
акустическую мощность на глубине R
в два раза превышающую акустическую
мощность, которая на той же глубине R
вызывает повышение температуры в тканях
на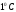 .
.
3.51.
Интервал времени между началом
зондирования и моментом прихода
эхо-сигнала затрачен ультразвуком на
прохождение до отражателя и обратно,
поэтому:
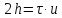 .
.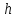 – глубина расположения отражателя.
– глубина расположения отражателя.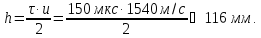
3.52. Частота допплеровского сдвига fd
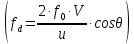 :
:
1)
пропорциональна частоте (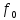 )
излучения;
)
излучения;
2)
пропорциональна скорости (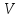 )
движения отражателя (рассеивателя);
)
движения отражателя (рассеивателя);
3)
обратно пропорциональна скорости (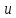 )
ультразвука в биологической ткани;
)
ультразвука в биологической ткани;
4)
зависит от углов
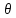 ,
образуемых вектором скорости с
направлениями излучения и приёма (в
частности, при θ = 90оfd
= 0).
,
образуемых вектором скорости с
направлениями излучения и приёма (в
частности, при θ = 90оfd
= 0).
3.53.
Увеличение затухания и возрастание
мощности рассеянного сигнала с ростом
частоты и ширины пучка делает оптимальным
выбор диапазона f0
2 -20 МГц. При этом частоты допплеровского
сдвига
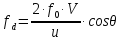 находятся практически в звуковом
диапазоне:
находятся практически в звуковом
диапазоне:
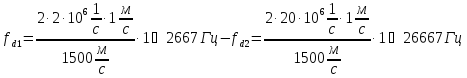 .
.
Ответ:
от
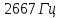 до
до .
.
4. ЭЛЕКТРОБИОЛОГИЯ
4.1. Решение. Согласно определению напряжённость электрического поля является характеристикой данной точки пространства. Электрическое поле считается заданным, если известна векторная величина (напряжённость электрического поля), однозначно определяющая силу, действующую на электрический заряд, помещённый в данную точку поля.
4.2. Решение. Термин напряжение означает разность электрических потенциалов, поэтому напряжение характеризует две точки поля. (Сам электрический потенциал, на самом деле, является разностью потенциалов потенциального электрического поля данной точки и точки, для которой потенциал выбран равным нулю.)
4.3.
Решение.
В качестве модели протонов примем
электрически заряженные шары. Учтём,
что протон является носителем элементарного
положительного заряда (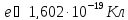 )
. Принятая модель позволяет применить
для электрического взаимодействия
формулу аналогичную формуле закона
Кулона (
)
. Принятая модель позволяет применить
для электрического взаимодействия
формулу аналогичную формуле закона
Кулона (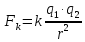 ),
а для гравитационного взаимодействия
формулу аналогичную формуле взаимодействия
точечных масс (
),
а для гравитационного взаимодействия
формулу аналогичную формуле взаимодействия
точечных масс (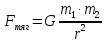 ).
В формуле электрического взаимодействия
).
В формуле электрического взаимодействия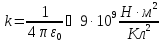 ,
,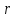 имеет один и тот же смысл расстояния
между двумя точками, а
имеет один и тот же смысл расстояния
между двумя точками, а Отношение двух сил:
Отношение двух сил:
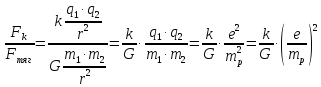 .
.
Ответ:
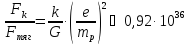 .
Десятичный логарифм отношения:
.
Десятичный логарифм отношения: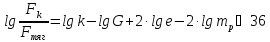 .
В данном случае полученный числовой
результат очень важен, он показывает,
что электрическое взаимодействие в
данном пространственно-временном
масштабе преобладает над гравитационным.
В масштабе человеческого организма это
соотношение сохраняется, иначе говоря,
из четырёх известных видов взаимодействия,
определяющих силовые взаимодействия,
важнейшим для процессов жизнедеятельности
организма являются электромагнитные
взаимодействия.
.
В данном случае полученный числовой
результат очень важен, он показывает,
что электрическое взаимодействие в
данном пространственно-временном
масштабе преобладает над гравитационным.
В масштабе человеческого организма это
соотношение сохраняется, иначе говоря,
из четырёх известных видов взаимодействия,
определяющих силовые взаимодействия,
важнейшим для процессов жизнедеятельности
организма являются электромагнитные
взаимодействия.
4.4.
Решение. Электростатический диполь
является электронейтральной системой,
состоящей из двух точечных электрических
зарядов противоположных по знаку и
одинаковых по величине, находящихся на
неизменном расстоянии друг от друга.
Расстояние между зарядами является
модулем вектора плеча диполя. Плечо
диполя
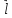 – вектор, направленный по линии,
соединяющей заряды, от отрицательного
к положительному заряду диполя.
Произведение модуля заряда на плечо
диполя образует вектор дипольного
момента электростатического диполя
– вектор, направленный по линии,
соединяющей заряды, от отрицательного
к положительному заряду диполя.
Произведение модуля заряда на плечо
диполя образует вектор дипольного
момента электростатического диполя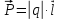 (Кл
(Кл м).
м).
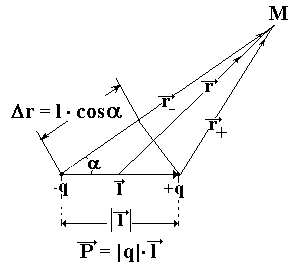 Для
того, чтобы рассчитать потенциал,
созданный диполем в точке М воспользуемся
известной формулой потенциала точечного
заряда
Для
того, чтобы рассчитать потенциал,
созданный диполем в точке М воспользуемся
известной формулой потенциала точечного
заряда
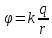 и принципом суперпозиции в электростатике.
Согласно принципу суперпозиции
результирующий потенциал будет равен
алгебраической сумме потенциалов,
создающих электростатическое поле.
и принципом суперпозиции в электростатике.
Согласно принципу суперпозиции
результирующий потенциал будет равен
алгебраической сумме потенциалов,
создающих электростатическое поле.
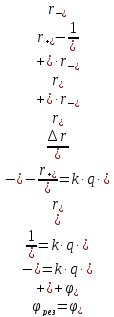 =
=
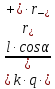 .
.
Для
тех точек пространства, для которых
выполняется условие:
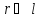 электростатический диполь считают
точечным и выведенная формула упрощается
до:
электростатический диполь считают
точечным и выведенная формула упрощается
до: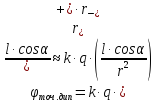 .
.
Ответ:
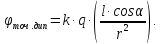
4.5. Решение.
По известному выражению для потенциала
поля точечного электростатического
диполя
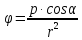 найдём модуль напряжённости поля. При
этом учтём, что особым выделенным
направлением в данном случае окажется
направление, совпадающее с направлением
дипольного моментаP.
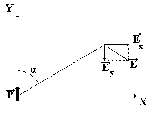
Если расположить диполь в пространстве
так, что он находится в начале координат
и направлен вдоль оси Y,
то картина силовых линий поля диполя
окажется одинаковой для любой плоскости,
проходящей через вектор дипольного
момента. φ и Ε симметричны относительно
оси Y.
найдём модуль напряжённости поля. При
этом учтём, что особым выделенным
направлением в данном случае окажется
направление, совпадающее с направлением
дипольного моментаP.
Если расположить диполь в пространстве
так, что он находится в начале координат
и направлен вдоль оси Y,
то картина силовых линий поля диполя
окажется одинаковой для любой плоскости,
проходящей через вектор дипольного
момента. φ и Ε симметричны относительно
оси Y.
Воспользуемся
связью напряжённости электростатического
поля с его потенциалом
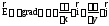 и найдём проекции вектора напряжённости
и найдём проекции вектора напряжённости
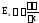 и
и
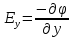 .
После чего модуль вектора напряженности
получится как:
.
После чего модуль вектора напряженности
получится как: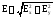 .
.
На
плоскости XY
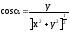 ,
,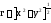 и
и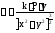 .
.
Для
проекции
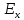 получим:
получим:
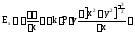
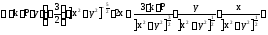
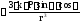 .
Для проекции
.
Для проекции
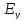 получим:
получим:
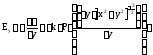

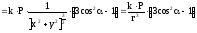 .
.
Итак:
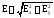 .
.
Иначе:
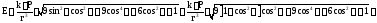
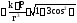 .
.
Ответ:
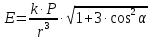 .
.
4.6.
Решение.
Считается известным, что потенциал
электростатического поля, созданного
точечным зарядом
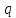 на расстоянии
на расстоянии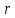 от него, определяется по формуле:
от него, определяется по формуле: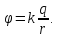 Записав эту формулу для двух расстояний,
где искомый потенциал
Записав эту формулу для двух расстояний,
где искомый потенциал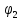 ,
расстояние
,
расстояние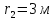 и разделив почленно выражение для
искомого потенциала на выражение для
известного потенциала, получим:
и разделив почленно выражение для
искомого потенциала на выражение для
известного потенциала, получим:
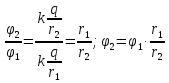 .
.
Ответ: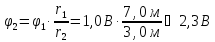
4.7.
Решение.
Считается известным, что потенциал
электростатического поля, созданного
точечным диполем на расстоянии
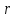 от него, определяется по формуле:
от него, определяется по формуле: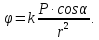 В этой формуле:P
–модуль вектора дипольного момента (
В этой формуле:P
–модуль вектора дипольного момента (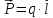 - дипольный момент диполя,
- дипольный момент диполя,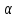 - угол между дипольным моментом и
вектором
- угол между дипольным моментом и
вектором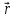 ).
Записав эту формулу для двух расстояний,
где искомый потенциал
).
Записав эту формулу для двух расстояний,
где искомый потенциал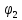 ,
расстояние
,
расстояние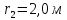 и разделив почленно выражение для
искомого потенциала на выражение для
известного потенциала, получим:
и разделив почленно выражение для
искомого потенциала на выражение для
известного потенциала, получим:
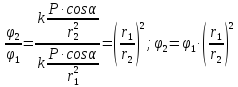 .
.
Ответ: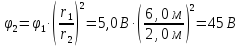
4.8.
Решение.
Считается известным, что напряжённость
электростатического поля, созданного
точечным электрическим зарядом на
расстоянии
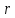 от него, определяется по формуле:
от него, определяется по формуле: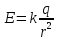 (вывод формулы студент должен знать).
В этой формуле:
(вывод формулы студент должен знать).
В этой формуле: – точечный электрический заряд. Записав
эту формулу для двух расстояний, где
искомая напряжённость
– точечный электрический заряд. Записав
эту формулу для двух расстояний, где
искомая напряжённость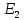 ,
расстояние
,
расстояние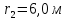 и разделив почленно выражение для
искомой напряжённости на выражение для
известной напряжённости, получим:
и разделив почленно выражение для
искомой напряжённости на выражение для
известной напряжённости, получим:
 .
.
Ответ: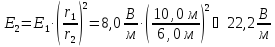 .
.
4.9.
Решение.
Считается известным, что напряжённость
электростатического поля, созданного
точечным электрическим зарядом на
расстоянии
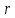 от него, определяется по формуле:
от него, определяется по формуле: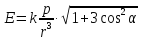 (вывод формулы студент должен знать).
В этой формуле:
(вывод формулы студент должен знать).
В этой формуле: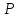 – модуль дипольного момента точечного
диполя. Записав эту формулу для двух
расстояний, где искомая напряжённость
– модуль дипольного момента точечного
диполя. Записав эту формулу для двух
расстояний, где искомая напряжённость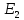 ,
расстояние
,
расстояние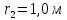 и разделив почленно выражение для
искомой напряжённости на выражение для
известной напряжённости, получим:
и разделив почленно выражение для
искомой напряжённости на выражение для
известной напряжённости, получим:
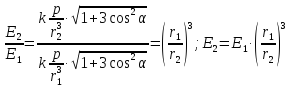 .
.
Ответ: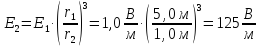 .
.
4.10.
Решение.
Поскольку, в данном случае, плечо диполя
l
= 100 нм в
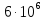 раз меньше расстоянияr
= 0,6 м, то диполь является точечным
электростатическим диполем. Считается
известным, что модуль напряжённости
электростатического поля, созданного
точечным электрическим диполем на
расстоянии
раз меньше расстоянияr
= 0,6 м, то диполь является точечным
электростатическим диполем. Считается
известным, что модуль напряжённости
электростатического поля, созданного
точечным электрическим диполем на
расстоянии
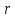 от него, определяется по формуле:
от него, определяется по формуле: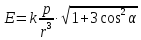 (вывод формулы студент должен знать).
В этой формуле:
(вывод формулы студент должен знать).
В этой формуле: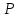 – модуль вектора дипольного момента
точечного диполя (
– модуль вектора дипольного момента
точечного диполя (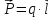 - дипольный момент диполя,
- дипольный момент диполя,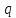 - модуль одного из зарядов, образующих
диполь,
- модуль одного из зарядов, образующих
диполь,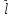 – плечо диполя,
– плечо диполя,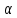 - угол между дипольным моментом и
вектором
- угол между дипольным моментом и
вектором ).
).
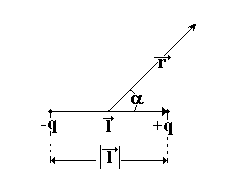
Итак:
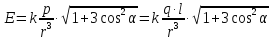 .
.
Ответ:
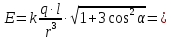
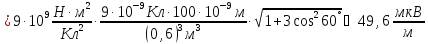 .
.
4.11.
Решение.
Поскольку, в данном случае, плечо диполя
l
= 100 нм в
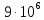 раз меньше расстоянияr
= 0,9 м, то диполь является точечным
электростатическим диполем. Считается
известным, что потенциал электростатического
поля, созданного точечным электрическим
диполем на расстоянии
раз меньше расстоянияr
= 0,9 м, то диполь является точечным
электростатическим диполем. Считается
известным, что потенциал электростатического
поля, созданного точечным электрическим
диполем на расстоянии
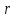 от него, определяется по формуле:
от него, определяется по формуле: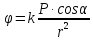 (вывод формулы студент должен знать).
В этой формуле:
(вывод формулы студент должен знать).
В этой формуле: – модуль вектора дипольного момента
точечного диполя (
– модуль вектора дипольного момента
точечного диполя (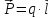 - дипольный момент диполя,
- дипольный момент диполя, - модуль одного из зарядов, образующих
диполь,
- модуль одного из зарядов, образующих
диполь,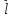 – плечо диполя,
– плечо диполя,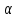 - угол между дипольным моментом и
вектором
- угол между дипольным моментом и
вектором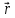 ).
).

Итак:
 .
.
Ответ:
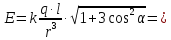
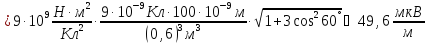 .
.
4.12. Решение. Вспомним, что в теории электростатического поля устанавливается связь вектора градиента потенциала и вектора напряженности электрического поля. Пользуясь определением градиента скалярной функции, запишем его общее выражение:
 ,
где
,
где
 – напряжённость электростатического
поля, а
– напряжённость электростатического
поля, а
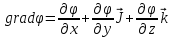
Направив
ось x
поперёк мембраны снаружи внутрь, поместив
0 на внешней поверхности клетки, получим
конкретное выражение для вектора
градиента: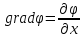 .
Изобразим график зависимости потенциала
от координатыx:
.
Изобразим график зависимости потенциала
от координатыx:
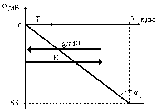
По
графику можно определить tgα.
Видно, что он отрицательный и равен
производной потенциала по координате
x.
Вычислим производную:
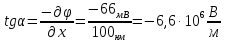 .
Сформулируем ответ:
.
Сформулируем ответ: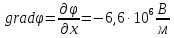 ,
т.е. вектор градиент потенциала направлен
наружу клетки и по модулю равен
,
т.е. вектор градиент потенциала направлен
наружу клетки и по модулю равен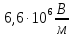 ,
а вектор напряжённости электрического
поля
,
а вектор напряжённости электрического
поля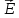 направлен внутрь клетки.
направлен внутрь клетки.
Ответ:
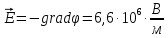 .
.
4.13.
Решение.
Реально, используя микроэлектродную
технику, измеряют разность потенциалов
между раствором вне клетки и раствором
внутри клетки. Закон изменения
электрического потенциала внутри
мембраны экспериментально не
устанавливается. В задаче сделано
предположение о том, что напряжённость
электрического поля в мембране постоянна.
Наша задача установить закон изменения
электрического потенциала в мембране.
Связь между электрическим потенциалом
и напряжённостью для электростатического
поля считаем известной
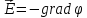 .
Для такого двумерного мира как мембрана
клетки потенциал должен зависеть только
от расстояния по перпендикуляру к
поверхности мембраны.
.
Для такого двумерного мира как мембрана
клетки потенциал должен зависеть только
от расстояния по перпендикуляру к
поверхности мембраны.
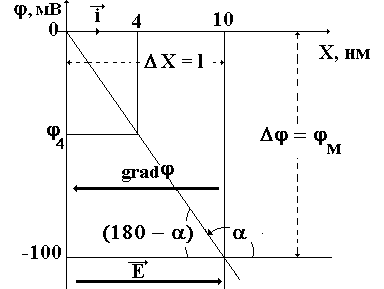
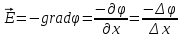 .
Постоянство поля означает, что
.
Постоянство поля означает, что
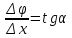 и зависимость потенциала от координаты
х линейная, такая как показанная на
рисунке. Из рисунка следует, что:
и зависимость потенциала от координаты
х линейная, такая как показанная на
рисунке. Из рисунка следует, что:
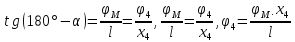 .
.
Ответ:
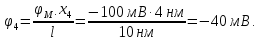
4.14.
Решение.
Считается известным, что модуль
напряжённости электростатического
поля, созданного точечным электрическим
диполем на расстоянии
 от него, определяется по формуле:
от него, определяется по формуле: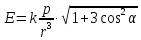 (вывод формулы студент должен знать).
В этой формуле:
(вывод формулы студент должен знать).
В этой формуле: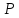 – модуль вектора дипольного момента
точечного диполя,
– модуль вектора дипольного момента
точечного диполя,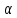 - угол между дипольным моментом и
вектором
- угол между дипольным моментом и
вектором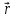 .
.
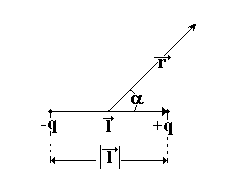
Итак:
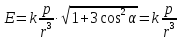 ,
откуда
,
откуда
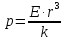 .
.
Ответ:
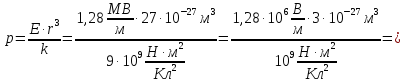
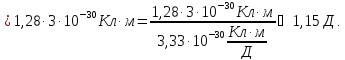
4.15.
Решение.
На диполь, помещённый в электрическое
поле, действует момент силы
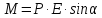 .
В формуле
.
В формуле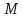 механический момент, действующий на
диполь,
механический момент, действующий на
диполь,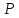 - дипольный момент диполя,
- дипольный момент диполя,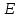 - напряжённость внешнего электрического
поля, в котором находится диполь,
- напряжённость внешнего электрического
поля, в котором находится диполь,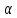 - угол между вектором дипольного момента
и вектором напряжённости внешнего
электрического поля. Максимальный
момент соответствует синусу равному
плюс единице, углу
- угол между вектором дипольного момента
и вектором напряжённости внешнего
электрического поля. Максимальный
момент соответствует синусу равному
плюс единице, углу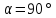 .
.
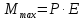 .
Напряжённость поля неподвижного
точечного заряда находится по формуле,
следующей из закона Кулона и определения
напряжённости электрического поля:
.
Напряжённость поля неподвижного
точечного заряда находится по формуле,
следующей из закона Кулона и определения
напряжённости электрического поля:
 .
Следовательно:
.
Следовательно: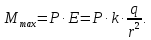
Ответ: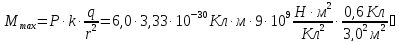
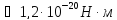 .
.
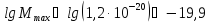 .
.
4.16.
Решение.
Рассчитаем работу сторонних сил, которую
они совершат над системой, чтобы повернуть
диполь. В соответствии с определением
элемент механической работы
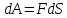 .
Если рассмотреть движение материальной
точки по окружности при действии
постоянной по величине силы,
.
Если рассмотреть движение материальной
точки по окружности при действии
постоянной по величине силы,
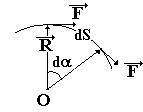
то
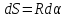 и
и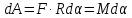 .
.
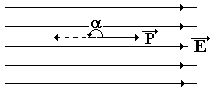
Элемент
работы при повороте объекта с дипольным
моментом получим, если учтём, что
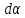 и момент сил поля противоположны по
знаку.
Для
поворота диполя элемент работы
и момент сил поля противоположны по
знаку.
Для
поворота диполя элемент работы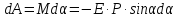
Конечная
работа сил поля:
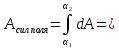
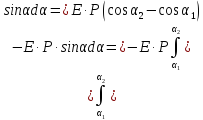
Конечная
работа сторонних сил будет равна работе
сил поля, взятой с противоположным
знаком: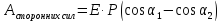
Ответ:
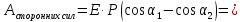 E∙P
E∙P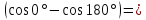
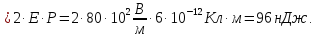
(Отметим, что силы электрического поля при этом повороте произведут отрицательную работу (-96 нДж)).
4.17.
Решение.
Рассчитаем работу сторонних сил, которую
они совершат над системой, чтобы повернуть
диполь. В соответствии с определением
элемент механической работы
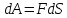 .
Если рассмотреть движение материальной
точки по окружности при действии
постоянной по величине силы,
.
Если рассмотреть движение материальной
точки по окружности при действии
постоянной по величине силы,

то
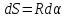 и
и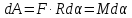 .
.
Элемент
работы при повороте объекта с дипольным
моментом получим, если учтём, что
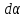 и момент сил поля противоположны по
знаку.
Для
поворота диполя элемент работы
и момент сил поля противоположны по
знаку.
Для
поворота диполя элемент работы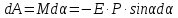
Конечная
работа сил поля:
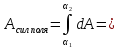
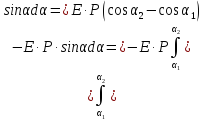
На
рисунке
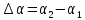 .
.
Ответ:
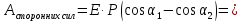 E∙P
E∙P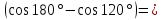
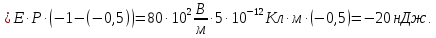
(Отметим, что силы электрического поля при этом повороте произведут положительную работу (+20 нДж)).
4.18.
Решение.
Если считать, что электрический заряд
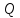 равномерно распределён по поверхности
Земли, то напряжённость электростатического
поля вне и на поверхности Земли:
равномерно распределён по поверхности
Земли, то напряжённость электростатического
поля вне и на поверхности Земли: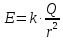 ,
гдеr
– расстояние от центра Земли. Применив
данную, получим:
,
гдеr
– расстояние от центра Земли. Применив
данную, получим:
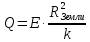 .
.
Ответ:
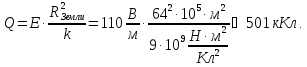
4.19.
Решение.
Если считать, что электрический заряд
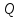 равномерно распределён по поверхности
Земли, то напряжённость электростатического
поля вне и на поверхности Земли:
равномерно распределён по поверхности
Земли, то напряжённость электростатического
поля вне и на поверхности Земли: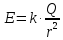 ,
гдеr
– расстояние от центра Земли. Соответственно
потенциал:
,
гдеr
– расстояние от центра Земли. Соответственно
потенциал:
 .
.
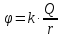 =
=
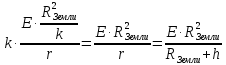 ,
гдеh
– высота над поверхностью Земли.
,
гдеh
– высота над поверхностью Земли.
Ответ:
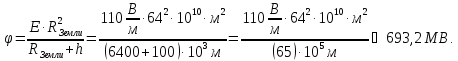
4.20. Решение.
Если считать, что электрический заряд
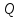 равномерно распределён по поверхности
Земли, то напряжённость электростатического
поля вне и на поверхности Земли:
равномерно распределён по поверхности
Земли, то напряжённость электростатического
поля вне и на поверхности Земли: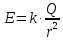 ,
гдеr
– расстояние от центра Земли. Соответственно
потенциал:
,
гдеr
– расстояние от центра Земли. Соответственно
потенциал:
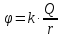 .
.
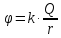 =
=
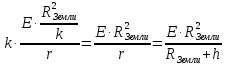 ,
гдеh
– высота над поверхностью Земли.
,
гдеh
– высота над поверхностью Земли.
Искомая разность потенциалов:
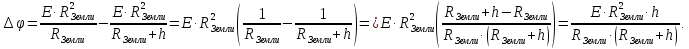
Ответ:
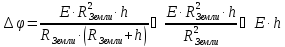 .
.
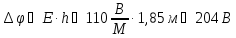 .
.
Тело человека в данном случае (электростатика) является проводником. Разность потенциалов между подошвами ног и макушкой головы человека равна нулю.
4.21.
Решение.
В однородном поле вектор напряжённости
электрического поля во всех точках поля
одинаков и направлен вдоль силовой
линии. Это значит, что работу можно
подсчитать по общей формуле для работы
постоянной силы на перемещении
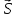 :
:
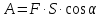 .
Применяя формулу для конкретного случая,
учтём
.
Применяя формулу для конкретного случая,
учтём
 ,
,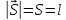 ,
,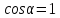 (
(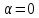 ).
Окончательно:
).
Окончательно: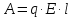 .
.
Ответ: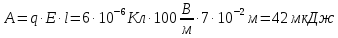 .
.
4.22.
Решение.
В однородном поле вектор напряжённости
электрического поля во всех точках поля
одинаков и направлен вдоль силовой
линии. Эквипотенциальные линии
располагаются перпендикулярно силовым
линиям. Это значит, что работу можно
подсчитать по общей формуле для работы
постоянной силы на перемещении
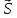 :
: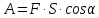 .
В нашем конкретном случае
.
В нашем конкретном случае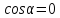 (
(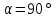 ).
С другой стороны, в потенциальном поле
работу можно подсчитать используя
разность потенциалов
).
С другой стороны, в потенциальном поле
работу можно подсчитать используя
разность потенциалов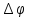 .
.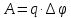 .При перемещении вдоль эквипотенциальной
линии
.При перемещении вдоль эквипотенциальной
линии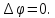 Окончательно:
Окончательно: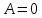 .
.
Ответ: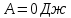 .
.
4.23.
Решение.
Известно, что напряжённость
электростатического поля равна взятому
с минусом градиенту потенциала.
Следовательно, модуль напряжённости
поля и модуль градиента потенциала в
данном случае составляют 300
В/см. Известно, что напряженность поля
между параллельными равномерно
заряженными бесконечными пластинами,
расположенными в вакууме:
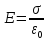 .
В формуле
.
В формуле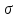 - поверхностная плотность заряда на
пластинах,
- поверхностная плотность заряда на
пластинах,
 электрическая постоянная. Заряд на
одной из пластин:
электрическая постоянная. Заряд на
одной из пластин:
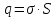 =
=
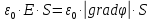 .
.
Ответ:
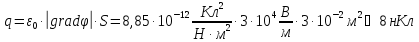
4.24.
Решение.
В качестве модели поля одновалентного
иона выберем поле точечного элементарного
заряда
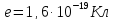 .
Напряжённость точечного заряда в вакууме
рассчитывается по формуле:
.
Напряжённость точечного заряда в вакууме
рассчитывается по формуле: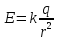 ,
где
,
где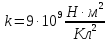 .
Окончательно:
.
Окончательно: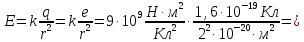
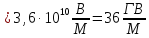 .
.
4.25.
Решение.
В качестве модели поля одновалентного
иона выберем поле точечного элементарного
заряда
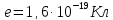 .
Потенциал точечного заряда в среде
рассчитывается по формуле:
.
Потенциал точечного заряда в среде
рассчитывается по формуле: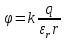 ,
где
,
где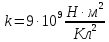 ,
а
,
а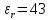 .
Окончательно:
.
Окончательно:
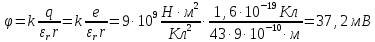 .
.
4.26. Решение. Выберем адекватную модель для расчёта напряжённости
электрического поля: одновалентный ион принять за точечный заряд.
Запишем
формулу модуля напряженности
электростатического поля точечного
заряда:
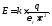 Определим электрический заряд
одновалентного иона: электрический
заряд одновалентного иона равен
положительному элементарному заряду.
Получим расчётную формулу:
Определим электрический заряд
одновалентного иона: электрический
заряд одновалентного иона равен
положительному элементарному заряду.
Получим расчётную формулу: Подставим в расчётную формулу числовые
значения, получим окончательный
результат:
Подставим в расчётную формулу числовые
значения, получим окончательный
результат: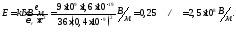
4.27.
Решение.
В качестве модели поля одновалентного
иона выберем поле точечного элементарного
заряда
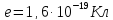 .
Потенциал точечного заряда в вакууме
рассчитывается по формуле:
.
Потенциал точечного заряда в вакууме
рассчитывается по формуле: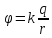 ,
где
,
где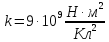 .
Окончательно:
.
Окончательно:
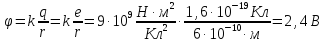 .
.
4.28. Решение. Электронная поляризация в диэлектриках практически не зависит от температуры.
4.29. Решение. Спонтанная поляризация в диэлектриках сильно зависит от температуры.
4.30. Решение. Ориентационная поляризация в диэлектриках зависит от температуры. Хаотическое тепловое движение интенсивность которого возрастает с увеличением температуры препятствует ориентационному действию внешнего поля.
4.31.
Решение.
Если представить себе ситуацию, при
которой внезапно включённое поле
оказывается действующим на произвольно
ориентированный диполь – молекулу, то
обнаружится возможность такого объекта
совершать крутильные колебания около
положения равновесия. Положение
равновесия в данном случае соответствует
ориентации вектора дипольного момента
по внешнему полю. При небольших
отклонениях от положения равновесия
на диполь будет действовать механический
крутящий момент
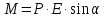 .
В формуле:
.
В формуле: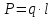 ,q
- элементарный заряд, l
– длина молекулы (она же модуль плеча
диполя).
,q
- элементарный заряд, l
– длина молекулы (она же модуль плеча
диполя).
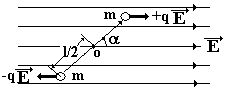
При
крутильных колебаниях наблюдается
аналогия с колебаниями пружинного
маятника. Возвращающая сила в пружинном
маятнике аналогична возвращающему
моменту крутильных колебаний. (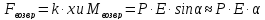 для малых колебаний).
для малых колебаний).
Смещение
от положения равновесия х в пружинном
маятнике аналогично углу поворота
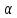 при крутильных колебаниях. Массаm
колеблющаяся в пружинном маятнике
аналогична моменту инерции крутильного
маятника
при крутильных колебаниях. Массаm
колеблющаяся в пружинном маятнике
аналогична моменту инерции крутильного
маятника
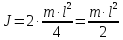 .
Руководствуясь отмеченной аналогией
составим уравнения динамики пружинного
маятника и крутильных колебаний.
.
Руководствуясь отмеченной аналогией
составим уравнения динамики пружинного
маятника и крутильных колебаний.
|
пружинный маятник |
крутильные колебания |
|
основное уравнение динамики. (третий закон ньютона) |
основное уравнение динамики вращательного движения |
|
|
|
|
круговая частота гармонических колебаний
|
круговая частота крутильных гармонических колебаний
|
|
период гармонических колебаний
|
период крутильных гармонических колебаний
|
Период
крутильных колебаний
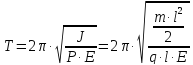 .
.
Ответ: