Нуралиева Мадина

Реферат на тему: «Модель Ходжкина-Хаксли»

Выполнила студентка МГМСУ 17 группа стом.фак.

Нуралиева М.

2012г

Модель Ходжкина — Хаксли — математическая модель, описывающая генерацию и распространение потенциалов действияв нейронах и других электрически возбуждаемых клетках — таких, например, как сердечные миоциты. Модель представляет собой комплекс ординарных дифференциальных уравнений, которая описывает характеристики электрического сигнала.

Модель была разработана Аланом Ллойдом Ходжкином и Эндрю Хаксли в 1952 году для описания электрических механизмов, которые обусловливают генерацию и передачу нервного сигнала в гигантском аксоне кальмара^[1]. За это авторы модели получили Нобелевскую премию в области физиологии и медицины за 1963 год.

Основные компоненты

Основные компоненты модели Ходжкина — Хаксли. Модель Ходжкина — Хаксли представляет собой биофизические характеристики клеточных мембран.

Компоненты электрической схемы, что соответствует модели Ходжкина — Хаксли, изображены на рисунке. В данной схеме каждый компонент возбуждаемой клетки имеет свой биофизический аналог. Внутреннему липидному слою клеточной мембраны соответствует электроёмкость (). Потенциал-зависимые ионные каналы отвечают за нелинейную электрическую проводимость (, где  — отдельный вид ионных каналов), это означает, что проводимость является потенциал-время-зависимой величиной. Эта составляющая системы, как было показано исследователями позже, реализуется благодаря белковым молекулам, которые образуют потенциал-зависимые ионные каналы, каждый из которых отмечен некоторой вероятностью открытия, величина которой зависит от электрического потенциала (или электрического напряжения) мембраны клетки. Каналы мембранных пор отвечают за пассивную проводимость (, где индекс  означаетангл. Leak — течь). Электрохимический градиент, побуждает ионы к движению через мембранные каналы, он показан с помощью аккумуляторов с соответствующим электродвижущей силой ( и ), величина которой определяется реверсивным потенциалом (англ.) для соответствующего вида иона. Ионные транспортеры соответствуют источникам тока ().

Производная по времени от мембранного потенциала клеточной мембраны () при описанных условиях пропорциональна сумме токов в полной электрической цепи. Она описывается следующим уравнением:

где  означает величину электрического тока, генерируемого отдельным видом ионов.

[править]Характеристики ионного тока

Электрический ток, проходящий через ионные каналы, может быть математически выражен следующим уравнением:

где  — равновесный потенциал -го ионного канала. В случае потенциал-зависимых ионных каналов канальная проводимость является функцией времени и потенциала (электрического напряжения) —  на рисунке, в то время как пассивная проводимость является величиной постоянной ( на рисунке). Ток, генерируемый ионными транспортерами, зависит от вида ионов, который переносит соответствующий транспортёр. Ниже приведено более подробное описание перечисленных величин:

Потенциал-зависимые ионные каналы

В терминах модели Ходжкина — Хаксли проводимость потенциал-зависимых каналов () описывается следующим образом:

где  и  являются константами скорости реакций закрытия и открытия каналов, соответственно. Они численно равны доле от максимальной возможной проводимости через данный вид каналов в каждый момент времени при каждой величине мембранного потенциала.  является максимальным возможным значением проводимости.  и  — константы,  и  — временны́е константы процессов активации и деактивации каналов, соответственно.  и  является стабилизированными значениями  и  при величине времени, стремящимся к бесконечности, и обычно рассчитываются из уравнения Больцмана как функции .

Для характеристики ионных каналов, последние два уравнения модифицируются для условий, когда на мембране поддерживается постоянная величина электрического потенциала — модификация уравнений Ходжкина — Хаксли, сделанная Марквардтом^[2] . Когда мембранный электрический потенциал поддерживается на постоянном уровне (voltage-clamp), для каждого значения этого потенциала нелинейные уравнения, описывающие пропуск ионов через каналы, редуцируются к линейных дифференциальных уравнений следующего вида:

Таким образом, для каждого значения мембранного потенциала , величина электрического тока описывается следующим уравнением:

Для аппроксимации кривых, которые генерируют данные уравнения, до значений клеточных токов при фиксированном значении мембранного потенциала используется алгоритм Левенберга — Марквардта^[3][4], что является модифицированным алгоритмом Гаусса — Ньютона.

[править]Пассивные каналы

Пассивные каналы отвечают за проницаемость мембраны для ионов в спокойном состоянии (не во время проведения потенциала действия), и ток через них описывается теми же уравнениями, что и для потенциал-зависимых каналов, но при условии постоянной величины проводимости  ().

[править]Ионные транспортеры

Мембранный электрический потенциал генерируется с помощью поддержания концентрационных градиентов ионов, присутствующих в физиологических жидкостях организма, относительно клеточной мембраны. Наиболее важными из белков-транспортеров, которые поддерживают мембранный потенциал, является натриево-кальциевый (транспортирует один ион Са²⁺внутрь клетки в обмен на 3 иона Na⁺ , транспортируемых наружу), натриево-калиевый (транспортирует один ион Na⁺ наружу в обмен на один ион К⁺ внутрь) и хлорный (транспортирует из клетки наружу ионы Cl⁻)^[5][6].

[править]Модификации и альтернативные модели

Модель Ходжкина — Хаксли является одним из важнейших достижений в биофизике и нейрофизиологии XX-го века. Со временем она была модифицирована в следующих направлениях:

• Основываясь на экспериментальных данных, в ней были инкорпорированы дополнительные виды ионных каналов и транспортеров.

• Основываясь на данных микроскопии высокого разрешения, в уравнение добавлены элементы, характеризующие сложную морфологию отростков нервных клеток (аксонов и дендритов).

Также на общих принципах модели Ходжкина — Хаксли были разработаны несколько моделей, описывающих взаимную активацию и деактивацию в нейронных сетях, а также молекулярную динамику генерации потенциала действия.

Уравнения Ходжкина –Хаксли: приемы моделирования

Уравнения Ходжкина –Хаксли: Вид нелинейностей

Равновесные потенциалы

VNa+ = 115mV

VK+ = -12mV

VL = 10.6 mV

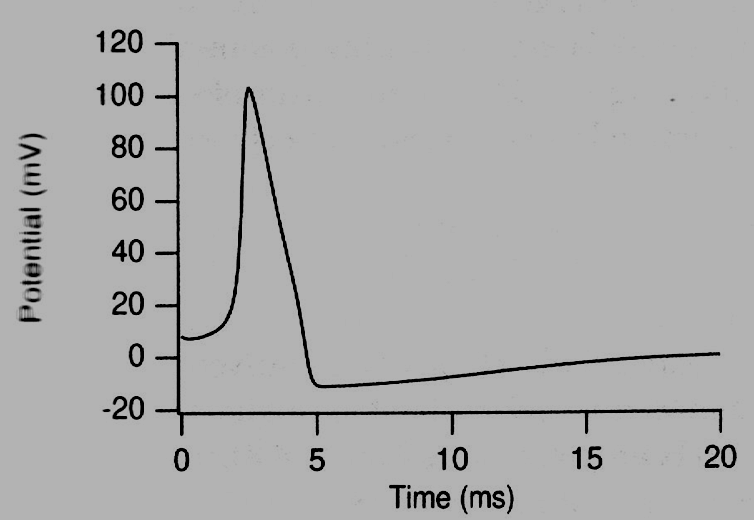
Уравнения Ходжкина –Хаксли:

Как все работает Равновесные потенциалы

Уравнения Ходжкина –Хаксли: Фазовое подпространство быстрых переменных (V-m)

Фазовое подпространство быстрой и медленной переменных (V-n)

Фазовое подпространство быстрых переменных (V-m)

Цикл генерации потенциала действия