llama / llama_bachelor_MPiTK_2004_VM-1

- 31-

Шаг 3. Построить разбиение Ωi = {ωk }kL=−10 множества обучающих векторов {am}, где ячейки разбиения определяются по текущей кодовой книге Ci = {cik }kL=−10 , следующим образом:

2.4. Общая схема алгоритма сжатия изображений

Разработанный алгоритм, как следует из сказанного выше, должен состоять из двух частей. В первой части строится кодовая книга, которая потом используется как начальная кодовая книга для алгоритма адаптивного векторного квантования. Для всех изображений, подлежащих сжатию, можно использовать одну и ту же кодовую книгу, а значит, первую часть алгоритма нужно запустить всего один раз и полученную на ее выходе кодовую книгу сохранить, например, в виде файла, который затем используется второй частью – как кодером, так и декодером. Таким образом, для сжатия изображения

- 32-

не требуется каждый раз запускать алгоритм, описанный в п.0, который обладает невысокой скоростью работы, а также хранить кодовую книгу вместе со сжатым файлом, что приводит к повышению битовых затрат.

Вторая часть алгоритма представляет собой обычную реализацию алгоритма GTR (п.1.2.6). Кодирование выходных потоков индексов и скалярно проквантованных

компонент векторов производится адаптивным многомодельным арифметическим кодером [1].

Баланс между качеством и сжатием при кодировании изображения определяется параметром λ , т.е. для каждого значения λ требуется построить свой набор кодовых книг.

2.4.1. Построение кодовых книг по обучающей последовательности векторов

Шаг 1. С помощью алгоритма, описанного в п.1.2.8, найти разбиение матрицы ДКП (8×8 ) на слабо коррелированные друг с другом подмножества (кластеры). Оптимальное число – 14 кластеров.

Шаг 2. Найти поблочное (8×8 ) ДКП обучающего изображения.

Шаг 3. В каждом из получившихся блоков преобразовать набор элементов, входящих в один и тот же кластер, в вектор. Векторы из всех блоков группируются в наборы по кластерам, которым они принадлежат*.

Шаг 4. Построить кодовые книги по каждому набору векторов, полученному на предыдущем шаге (всего 14 книг) с помощью алгоритма, описанного в п.0. Вместе с n -й

кодовой книгой вычисляется и массив вероятностей кодовых векторов { pk0}Lkn=−01 , который далее используется при кодировании.

- 34-

{aˆupdatek }kN=0 кодируются в одной модели. Отдельные модели используются также для

кодирования постоянной составляющей и номеров скалярных квантователей, с помощью которых проводилось квантование.

Шаг 6. Выходной поток данных выводится в файл побайтно в двоичном виде.

Конец.

Декодирование изображения производится в обратном порядке.

2.5. Реализация алгоритма сжатия изображений

Описанный в предыдущем параграфе алгоритм был реализован на языке пакета MATLAB 6.5 с использованием дополнительных наборов функций Image Processing Toolbox и External Interfaces API. Наиболее критичные для производительности алгоритма функции – поблочное ДКП, поиск в кодовой книге вектора с минимальным значением J методом полного перебора и алгоритм GTR – были реализованы на языке C и скомпилированы компилятором CL производства Microsoft в MEX-библиотеки, используемые средой MATLAB. Для реализации арифметического кодера были использованы оригинальные исходные тексты программы на языке C++, описанной в

[1].Они также были скомпилированы в виде MEX-библиотеки.

2.6.Сравнение алгоритма с существующими методами сжатия изображений

2.6.1. Условия тестирования

Реализованный алгоритм сравнивался со стандартным методом JPEG и его модификацией, использующей вместо кодирования Хаффмана арифметическое кодирование. Работа алгоритма тестировалась при различных параметрах: изменялось число кластеров, размеры кодовых книг, параметр λ , величины скалярных квантователей.

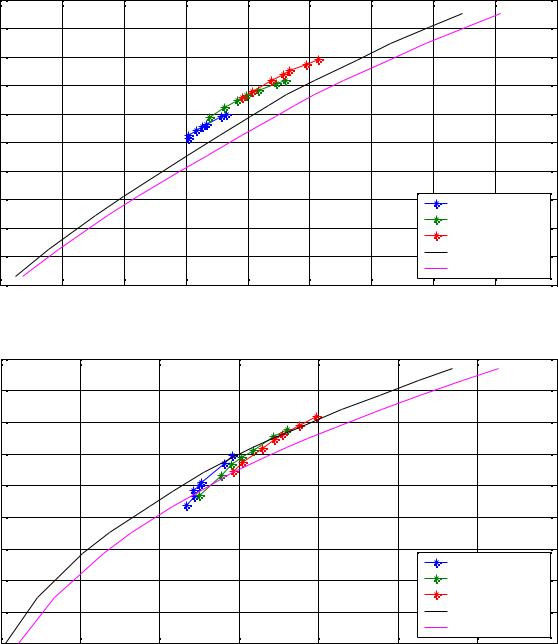
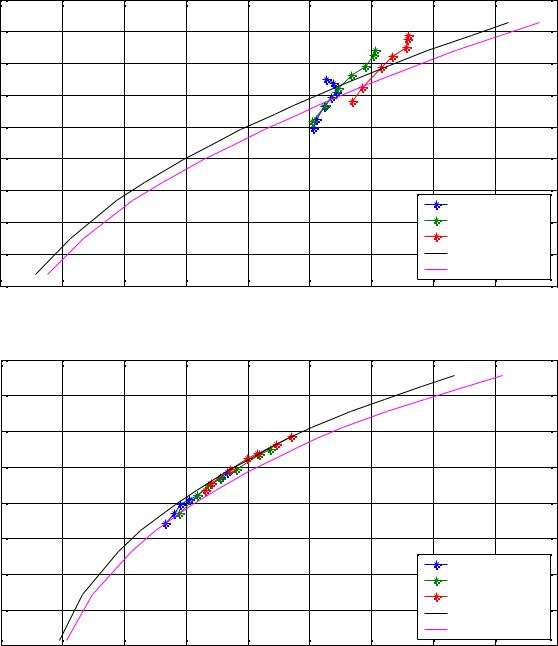
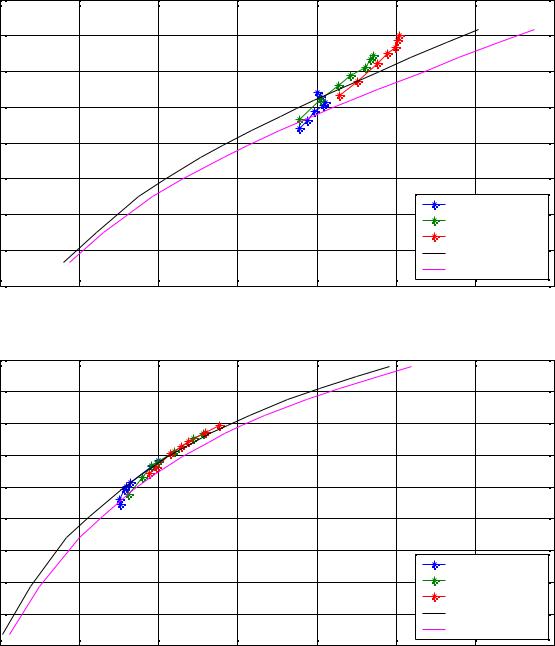
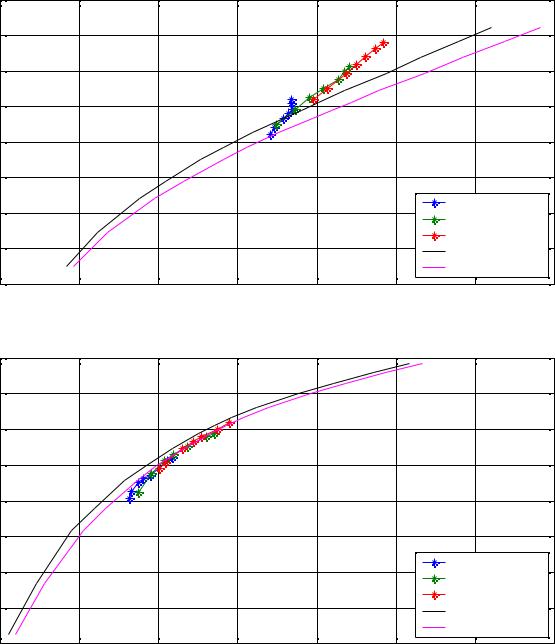
Эксперименты проводились на девяти тестовых изображениях: Barbara, Boat, Cathedral, Goldhill, House, Lena, Mandrill, Peppers и Zelda. Для оценки качества сжатия изображения использовалась оценка PSNR (см. п.1.2.2). Мерой битовых затрат являлось число бит, затраченное на кодирование изображения, приходящихся на 1 пиксель (bits

per pixel): BPP = MN8S , где S – размер файла в байтах, а M,N – размеры изображения в пикселях. На всех графиках буквой L обозначены длины кодовых книг. Приведены

- 40-

Также проведен обзор теоретических основ сжатия изображений с потерями, в частности, основ векторного квантования.

Существует несколько направлений дальнейшей работы по улучшению созданного алгоритма. Во-первых, возможно использование контекстного кодирования для постоянной составляющей ДКП. Во-вторых можно применять вместо ДКП другие ортогональные преобразования, например, ДВП, так как предлагаемый алгоритм векторного квантования является универсальным и при кодовой книге, построенной по соответствующим обучающим векторам, может использоваться для сжатия любых данных. В-третьих, для более эффективного кодирования индексов векторов можно воспользоваться алгоритмом группировки индексов [10]. В-четвертых, можно использовать контекстное кодирование как индексов векторов, так и скалярно проквантованных их компонент.