
llama / llama_bachelor_MPiTK_2004_VM-1
.pdf
- 21- (в широком смысле) дискретного процесса означает, что отсчёты дискретного сигнала
{Xk } имеют |
одинаковые |
математические |
ожидания M ( Xk ) = mX |
|
и |
дисперсии |
||
D( Xk ) = σ X2 , |
а корреляция |
между отсчетами |
Xk , X j зависит только |
|
от |
расстояния |
||
между моментами наблюдения дискретного процесса, т.е. от величины |
|
k - j |
|
. Так, для |
||||
|
|
|||||||
марковского процесса первого порядка коэффициент корреляции r (Xk , X j ) = ρ k − j , где
ρ – коэффициент |
корреляции соседних отсчётов сигнала. Тогда случайный вектор |
|||||||||
X = ( X0 ,K, X N −1 )T |
– выборка |
|
из |
дискретного сигнала, описываемого моделью |
||||||
марковского процесса, имеет следующую ковариационную матрицу: |
|
|||||||||
|
|
æ |
|
1 |
|
ρ |
K ρ N −1 |
ö |
|
|
|
2 |
ç |
|
ρ |
|
1 |
K ρ N −2 |
÷ |
(6) |
|
|
KX (ρ ) = σ X |
ç |
K |
K |
1 |
K |
÷ . |
|||
|
|
ç |
ρ |
N −1 |
ρ |
N −2 |
K |
1 |
÷ |
|
|
|
è |
|
|
ø |
|
||||
Модель (6) представляет особый интерес, так как часто используется на практике для описания дискретных сигналов, причём обычно параметр ρ имеет значение,
близкое к единице.
1.4.4. Дискретное косинусное преобразование
Среди |
преобразований, имеющих быстрые алгоритмы вычислений (требующих |
! N log N |
операций умножения вместо ! N 2 ), наибольшую эффективность для |
кодирования сигнала, описываемого моделью марковского процесса, показывает
дискретное косинусное преобразование (ДКП), которое определяется следующей формулой:
|
|
|
|
|
|
|
|
|
2 |
|
|
N −1 |
æ π k |
æ |
|
1 öö |
|
|
||||||
|
|
|
|
|
yk |
= |
|
|
c(k )åxj |
cosç |
ç |
j + |
|
÷÷ |
, |
(7) |
||||||||
|
|
|
|
N |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
j=0 |
|
|
|
|
è N |
è |
|
2 øø |
|
||||
где |
|
|
|
|
|
|
|
|
|
|
k = 0,1,K, N −1, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì 1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
c(k ) |
= íï |
|
|
|
|
|
, при k = 0 . |
|
|
|
(8) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
1, при k ¹ 0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|||||
Записав ДКП (7) в матричном виде, Y = WX, получим для структуры матрицы ДКП: |
||||||||||||||||||||||||
ì |
|
|
|
|
|
æ |
π k æ |
|
|
|
|
üN −1 |
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ï |
|
|
|
|
|
|
1 ööï |
|
|
|
|
|
|
|
|
|
||||||||
W = íwk , j |
= |
|
|
c(k )cosç |
|
|
ç j + |
÷÷ý |
. |
|
|
|
|
|
|
|||||||||
N |
N |
|
|
|
|
|
|
|||||||||||||||||
ï |
|
|
|
|
è |
è |
|
|
2 øøï |
|
|
|
|
|
|
|
|
|
||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
þk , j=0 |
|
|
|
|
|
|
||||
- 22-
Важным свойством ДКП является его ортогональность: WT = W−1 . Следовательно, для него выполняется соотношение (5). Обратное ДКП определяется формулой:
|
|
|
2 |
|
N −1 |
æ π k æ |
|
1 öö |
|
|
|||
xj |
= |
|
|
|
åc(k ) yk |
cosç |
N |
ç |
j + |
|
÷÷ |
, |
(9) |
|
2 |
||||||||||||
|
|
|
N j=0 |
è |
è |
|
øø |
|
|||||
j = 0,1,K, N −1.
Для стационарного марковского процесса первого порядка по сравнению с такими преобразованиями как дискретное преобразование Фурье (ДПФ) в вещественной форме, дискретные преобразования Уолша (ДПУ) и Хаара (ДПХ), ДКП дает наиболее близкие к оптимальному преобразованию Карунена-Лоэва характеристики.
1.5. RD-оптимизация
Пусть x – некоторый набор входных данных, которому в результате выполнения процедуры сжатия-восстановления ставится в соответствие выходной набор данных той же природы, y = F (x,u), где u = (u1,...,un ) – набор управляющих параметров алгоритма кодирования с потерями; x,y – элементы некоторого метрического пространства Ω с
метрикой |
D( X ,Y ), U |
– множество всех возможных значений управляющего вектора |
|||
u , т.е. |
xΩ, y Ω, u U . Задача |
оптимизации алгоритма |
F |
формулируется |
|
следующим образом: |
для заданного |
набора входных данных |
x |
и максимально |
|
допустимой длины выходного двоичного кода Rb найти такие параметры u = (u1 ,...,un )
алгоритма F , чтобы ошибка кодирования данных, т.е. величина D(x,y) = D(x, F (x,u)),
принимала бы минимальное значение. То есть
D(x, F (x,u )) = D(x,u ) = min (D(x,u)), |
|
|
|
u U |
, |
(10) |
|
R(x,u ) £ Rb , |
|||
|
|
где R(x,u) – число бит, необходимое для кодирования набора данных x по алгоритму
F при выбранных параметрах u = (u1,...,un ) . Множество U можно интерпретировать
как некоторое подмножество n-мерного евклидова пространства En . Для простоты положим, что множество U совпадает со всем пространством En (при необходимости,
функции D(x,u), R(x,u) можно доопределить на множестве En \U ). Если,
дополнительно, определенные на множестве U функции D(x,u), R(x,u) также
выпуклы (для любых фиксированных значений x), то (10) представляет собой задачу выпуклого математического программирования.
- 23- |
|
Для решения задачи (10) воспользуемся |
теоремой Куна-Таккера [2]: пусть |
f (x1,..., xn ) ® min, gi (x) £ 0, i = 1,...,m – задача |
выпуклого программирования с |
множеством U , определенным ограничениями, имеющим хотя бы одну внутреннюю точку (т.е. множество U удовлетворяет условию Слейтера). Тогда для того, чтобы точка x ÎU была решением этой задачи, необходимо и достаточно, чтобы существовал вектор множителей Лагранжа λ Î Em с неотрицательными координатами, такой, что
L |
( |
x ,λ |
) |
x En |
( |
x,λ |
) |
; |
|
|
|
= min L |
|
|
|||||
λi gi (x ) |
= 0, i = 1,...,m. |
, |
|||||||
|
|||||||||
m |
|
|
|
|
|
|
|
|
|
где L(x,λ ) = f (x) + åλi gi (x) |
– функция Лагранжа. |
||||||||
i=1 |
|
|
|
|
|
|
|
|
|
Согласно этой теореме, поиск решения задачи (10) сводится к безусловной
минимизации функции Лагранжа
L(u,λ ) = D(u) + λ (R(u) - Rb ) , т.е. L(u ,λ ) = min L(u,λ ),
u En
где константа λ ³ 0 такова, что λ (R(u) - Rb ) = 0 . Здесь функции D(x,u), R(x,u) для краткости обозначены как D(u), R(u) .
Если u является решением задачи (10), то u является также решением задачи
условной минимизации
D(u ) = min (D(u)),
u U
R(u) = Rb/ ,
где Rb/ = Rb - (Rb - R(u )) = R(u ). Т.е. если известна заранее величина Rb/ , то для случая U = En решение (10) является так же решением задачи безусловной
минимизации по параметрам u функции
L(u) = D(u) + λ (R(u) - Rb/ )
или
|
|
|
|
|
J (u) = D(u) + λR(u) , |
|
|
|
(11) |
|||||||||
где множитель Лагранжа λ |
определяется некоторым образом по величине R / |
. Таким |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
образом, при U = En решению u |
исходной задачи (10) соответствует параметр λ , при |
|||||||||||||||||
котором |
( |
|
) |
|
|
( |
|
) |
|
ë |
( |
|
) |
|
( |
|
)û |
(12) |
J |
u |
= min J |
u |
|
u |
+ λR |
u |
|||||||||||
|
|
|
|
= min éD |
|
|
|
ù . |
|
|||||||||
|
|
|
|
|
u |
|
|
|
u |
|
|
|
|
|
|
|
|
|
- 24-
Минимизация функции (11) лежит в основе подхода, используемого на практике при оптимизации схем кодирования. Кроме того, вводится дополнительное ограничение:
при любом изменении вектора параметров u величины R(u) и D(u) не могут одновременно уменьшаться или одновременно увеличиваться, и, поскольку всегда
R(u) ³ 0 и D(u) ³ 0 , отсюда следует, что параметр λ в функции (11) устанавливает баланс между качеством и уровнем сжатия данных. Увеличивая значение λ при оптимизации алгоритма по (12), получим меньшую длину кода, но большую ошибку.
Значение |
λ = 0 соответствует наименьшей возможной ошибке кодирования, значение |
λ = ∞ – |
наибольшему сжатию. Это дает возможность настраивать алгоритм на |
необходимые характеристики.
Таким образом, определение оптимальных параметров u алгоритма кодирования F может быть сведено к процедуре минимизации, имеющей общий вид (12). Данная процедура называется RD-оптимизацией (Rate – Distortion). Более подробно она описана в монографии [5].
-25-
2.Разработка алгоритма сжатия изображений
2.1.Краткий обзор существующих подходов
Как показано в п.1.2.4, векторное квантование является асимптотически оптимальным по битовым затратам на кодирование. Поэтому логично попытаться применить его в алгоритмах сжатия изображений. Однако при этом необходимо учитывать ограничения, связанные с невысокой скоростью работы векторного квантователя.
Векторное квантование можно применять для сжатия изображений в различных схемах. Например, квантование можно проводить как непосредственно в области изображения, так и в области его спектра, полученного в результате ортогонального преобразования изображения. Можно использовать различные преобразования; самыми распространенными являются дискретное косинусное преобразование (ДКП) и дискретное вейвлет-преобразование (ДВП).
Существует достаточно большое число алгоритмов сжатия изображений, использующих векторное квантование, в частности, алгоритмы TSMVQ [17], FS-RVQ [13], и Hybrid VQ [16]. Ни один из них не использует дискретное косинусное преобразование, в том числе и потому, что оно проводится над блоками достаточно больших размеров (минимум 16 элементов), что значительно замедляет работу векторного квантователя (см. п.1.2.7).
В настоящей работе использован способ уменьшения размерности векторов,
подвергаемых квантованию с помощью особого разбиения матрицы ДКП на непересекающиеся подмножества (кластеры). После проведения такого разбиения
появляется возможность использовать векторное квантование для кодирования коэффициентов ДКП.
Алгоритм [4] ранее не был апробирован, поэтому в рамках данной работы было проведено его исследование и тестирование на реальных данных.
2.2.Тестирование алгоритма кластеризации
Спомощью алгоритма [4] была обработана последовательность из нескольких десятков тысяч 64-компонентных векторов – поблочных ДКП-спектров нескольких тестовых фотографических изображений. Корреляционная матрица строилась по этим же векторам.
-26-
Втаблице приведена часть корреляционной матрицы для первых пяти НЧ- компонент блока ДКП 8×8 , развернутого в вектор с помощью «зигзаг-сканирования» так, как это выполняется в методе JPEG. Компоненты пронумерованы по столбцам блока.
Таблица 2.1. Корреляционная матрица НЧ-компонент спектра ДКП
№ компоненты |
1 |
2 |
|
9 |
|
17 |
10 |
|
|
|
|
|
|
|
|
|
|
1 |
1.0000 |
0.0048 |
|
0.0050 |
|
-0.0963 |
-0.0130 |
|
|
|
|
|
|
|
|
|
|
2 |
0.0048 |
1.0000 |
|
0.0410 |
|
-0.0043 |
0.0089 |
|
|
|
|
|
|
|
|
|
|
9 |
0.0050 |
0.0410 |
|
1.0000 |
|
0.0108 |
0.0058 |
|
|
|
|
|
|
|
|
|
|
17 |
-0.0963 |
-0.0043 |
|
0.0108 |
|
1.0000 |
0.0278 |
|
|
|
|
|
|
|
|
|
|
10 |
-0.0130 |
0.0089 |
|
0.0058 |
|
0.0278 |
1.0000 |
|
|
|
|
|
|
|
|
|
|
При изменении |
параметра |
Hmax были |
получены |
разбиения |
ДКП-спектра на |
|||
различное число кластеров, от 2 до 20. Постоянная составляющая не участвовала в кластеризации.
Эмпирическим путем было установлено, что разбиение на 14 кластеров дает наилучшие результаты в исследованном алгоритме сжатия изображений.
Таблица 2.2. Разбиение на 3 кластера Таблица 2.3. Разбиение на 4 кластера
0 |
3 |
|
2 |
3 |
|
2 |
|
3 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
1 |
3 |
|
1 |
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
2 |
1 |
|
2 |
|
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
1 |
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
2 |
1 |
|
2 |
|
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
1 |
3 |
|
1 |
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
3 |
3 |
|
2 |
|
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
3 |
3 |
|
3 |
|
3 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|||
|
Hmax = 108.95; H1 = 107.28; |
|
|
||||||||
|
H2 |
= 106.2; H3 |
= 93.5 |
|
|
|
|
||||
0 |
|
3 |
|
2 |
|
3 |
2 |
|
3 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
4 |
3 |
|
4 |
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
2 |
|
1 |
2 |
|
1 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
4 |
1 |
|
4 |
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
2 |
|
3 |
2 |
|
1 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
4 |
3 |
|
4 |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
3 |
|
4 |
|
3 |
4 |
|
3 |
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
3 |
|
4 |
3 |
|
4 |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Hmax |
= 80.95; H1 = 78.4; |
H2 |
= 67.4; |
|
|||||||||
H3 |
= 80.9; H4 |
= 80.3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|

- 27-
Таблица 2.4. Разбиение на 5 кластеров
0 |
|
1 |
|
2 |
|
1 |
|
2 |
|
5 |
|
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
3 |
|
4 |
|
3 |
|
4 |
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
2 |
|
1 |
|
2 |
|
1 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
3 |
|
4 |
|
3 |
|
4 |
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
2 |
|
1 |
|
2 |
|
1 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
3 |
|
4 |
|
3 |
|
4 |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
5 |
|
5 |
|
5 |
|
5 |
|
5 |
|
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
5 |
|
5 |
|
5 |
|
3 |
|
5 |
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||
Hmax |
= 65.95; H1 = 65.93; |
H2 = 62.4; |
|
|||||||||||
H3 |
= 64.9; H4 |
= 58.1; H5 = 55.7 |
|
|||||||||||
Таблица 2.6. Разбиение на 8 кластеров |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
6 |
|
3 |
|
6 |
|
7 |
|
8 |
|
7 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
4 |
|
5 |
|
2 |
|
5 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
6 |
|
3 |
|
6 |
|
2 |
|
5 |
|
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
4 |
|
5 |
|
2 |
|
5 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
6 |
|
3 |
|
6 |
|
2 |
|
6 |
|
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
4 |
|
5 |
|
2 |
|
8 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
8 |
|
7 |
|
7 |
|
7 |
|
8 |
|
2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
7 |
|
8 |
|
7 |
|
8 |
|
7 |
|
8 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||||
Hmax |
= 52.0; H1 = 43.28; H2 |
= 39.99; |
|
|||||||||||
H3 |
= 37.27; H4 = 36.79; H5 |
= 34.81; |
|
|
||||||||||
H6 |
= 46.49; H7 |
= 37.4; H8 |
= 31.42; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.5. Разбиение на 6 кластеров
0 |
1 |
3 |
|
1 |
3 |
|
6 |
5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
4 |
|
2 |
4 |
|
5 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
3 |
|
1 |
3 |
|
1 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
4 |
|
2 |
6 |
|
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
6 |
3 |
|
1 |
3 |
|
1 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
4 |
|
2 |
4 |
|
5 |
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
5 |
6 |
5 |
|
6 |
5 |
|
6 |
5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
6 |
5 |
6 |
|
5 |
6 |
|
5 |
6 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
Hmax |
= 60.0; H1 = 59.996; |
H2 = 52.2; |
|
|
||||||
H3 = 57.98; H4 |
= 55.9; H5 |
= 37.9; H6 |
= 43.5 |
|||||||
Таблица 2.7. Разбиение на 10 кластеров
0 |
6 |
5 |
6 |
8 |
7 |
10 |
7 |
|
|
|
|
|
|
|
|
3 |
1 |
3 |
1 |
4 |
2 |
4 |
2 |
|
|
|
|
|
|
|
|
5 |
6 |
5 |
6 |
2 |
4 |
2 |
4 |
|
|
|
|
|
|
|
|
3 |
1 |
3 |
1 |
4 |
2 |
4 |
2 |
|
|
|
|
|
|
|
|
8 |
7 |
8 |
6 |
2 |
7 |
2 |
4 |
|
|
|
|
|
|
|
|
9 |
1 |
9 |
1 |
4 |
10 |
9 |
10 |
|
|
|
|
|
|
|
|
8 |
7 |
8 |
7 |
8 |
7 |
2 |
7 |
|
|
|
|
|
|
|
|
9 |
10 |
9 |
10 |
9 |
10 |
9 |
10 |
|
|
|
|
|
|
|
|
Hmax = 37.0; H1 = 36.79; H2 = 36.6; H3 = 32.38; H4 = 34.81 H5 = 24.6;
H6 = 36.41; H7 = 31.68; H8 = 31.55; H9 = 24.22; H10 =18.54.
- 28-
Таблица 2.8. Разбиение на 12 кластеров
0 |
6 |
4 |
6 |
10 |
7 |
10 |
11 |
|
|
|
|
|
|
|
|
2 |
8 |
2 |
5 |
3 |
1 |
3 |
1 |
|
|
|
|
|
|
|
|
4 |
6 |
4 |
6 |
1 |
3 |
1 |
3 |
|
|
|
|
|
|
|
|
2 |
8 |
2 |
5 |
3 |
1 |
3 |
1 |
|
|
|
|
|
|
|
|
11 |
7 |
11 |
6 |
1 |
7 |
1 |
7 |
|
|
|
|
|
|
|
|
9 |
5 |
9 |
5 |
9 |
12 |
9 |
8 |
|
|
|
|
|
|
|
|
11 |
7 |
10 |
7 |
10 |
7 |
10 |
7 |
|
|
|
|
|
|
|
|
11 |
8 |
9 |
8 |
9 |
8 |
9 |
8 |
|
|
|
|
|
|
|
|
Hmax = 36.6; H1 = 34.59; H2 = 32.38; H3 = 28.59; H4 = 24.62 H5 = 21.66;
H6 = 36.41; H7 = 30.10; H8 = 25.26; H9 = 24.16; H10 = 20.85; H11 = 25.7; H12 = 3.42.
Таблица 2.9. Разбиение на 14 кластеров
0 |
8 |
2 |
6 |
11 |
12 |
11 |
12 |
|
|
|
|
|
|
|
|
3 |
10 |
3 |
5 |
7 |
9 |
4 |
9 |
|
|
|
|
|
|
|
|
2 |
8 |
2 |
6 |
1 |
4 |
1 |
4 |
|
|
|
|
|
|
|
|
13 |
10 |
3 |
5 |
13 |
1 |
4 |
9 |
|
|
|
|
|
|
|
|
14 |
8 |
14 |
6 |
1 |
4 |
1 |
12 |
|
|
|
|
|
|
|
|
7 |
5 |
7 |
5 |
7 |
9 |
7 |
9 |
|
|
|
|
|
|
|
|
14 |
12 |
11 |
12 |
11 |
12 |
11 |
12 |
|
|
|
|
|
|
|
|
13 |
10 |
13 |
10 |
13 |
10 |
13 |
10 |
|
|
|
|
|
|
|
|
Hmax = 25.85; H1 = 23.4; H2 = 24.6; H3 = 24.18; H4 = 21.37 H5 = 21.67;
H6 = 18.66; H7 = 23.63; H8 = 23.77; H9 = 16.58; H10 = 23.42; H11 = 20.8; H12 = 23.9 H13 = 24.14; H14 = 17.82.
Для проверки эффективности реализованного алгоритма описанный в п.2.4 метод сжатия изображений был протестирован.с различными разбиениями. Использовалось разбиение на 3 кластера, приведенное в таблице 2.2, а также два «интуитивных» разбиения, показанных в таблицах 2.8 и 2.9.
Таблица 2.10. «Интуитивное» разбиение 1 Таблица 2.11. «Интуитивное» разбиение 2
0 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
|
|
|
|
|
|
|
|
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
1 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
1 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
0 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
3 |
3 |
1 |
1 |
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
3 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
3 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
3 |
3 |
1 |
1 |
1 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
В качестве тестового использовалось изображение Goldhill; по нему же строилась и кодовая книга. Адаптивность алгоритма компрессии изображений на время тестирования была отключена. Таким образом, в данном тесте использовалось исключительно векторное квантование.
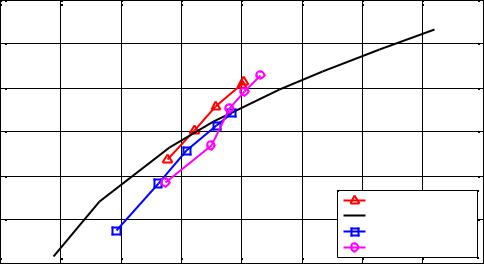
Результаты тестирования приведены на рисунке.
|
|
|
|
|
- 29- |
|
|
|
|
|
32 |
|
Goldhill, Clusters=3, L=[16 32 64 96 128 ] |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
dB |
|
|
|
|
|
|
|
|
|
PSNR, |
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Algorithm, λ=1.5 |
|
|
|
27 |
|
|
|
|
|
JPEG Huffman |
|
|
|
|
|
|
|
|
|
Intuitive 1, λ=0.92 |
|
|
|
26 |
|
|
|
|
|
Intuitive 2, λ=0.92 |
|
|
|
0.1 |
0.15 |
0.2 |
0.25 |
0.3 |
0.35 |
0.4 |
0.45 |
|
|
0.05 |
||||||||
|
|
|
|
|
BPP |
|
|
|
|
Как видно из графиков, алгоритм [4] дает лучший результат. Преимущество не так |
|||||||||
велико из-за хороших декоррелирующих свойств ДКП, однако оно дает до 13% |
|||||||||
выигрыша по сравнению с «интуитивными» разбиениями на кластеры. |
|
||||||||
2.3. Задание начальной кодовой книги алгоритма LBG
Как было указано в п.1.2.5, недостатком алгоритма LBG является сильная зависимость результата от начальной кодовой книги. Существующие способы ее построения часто приводят к недостаточно хорошим результатам. Поэтому для
повышения эффективности кодирования изображения предлагается новый способ построения начальной кодовой книги, названный условным разделением с шагом в случайном направлении. Он доказал свою эффективность по сравнению с существующими способами.
Этот способ напоминает обычное «разделение» кодовой книги с двумя отличиями. Во-первых, за одну итерацию разделяются не все векторы, а лишь один из них (перебор идет по очереди), после чего он заносится в текущую кодовую книгу. После разделения вектора запускается алгоритм LBG с текущей кодовой книгой в качестве начальной; в процессе его работы вычисляется суммарное значение J probe = D + λR при кодировании всех векторов обучающей последовательности с помощью новой кодовой книги. После этого полученное значение J probe сравнивается со значением J на предыдущей итерации. Если J probe > J , то только что добавленный вектор удаляется из кодовой книги и алгоритм переходит на следующую итерацию. Таким образом, добавление
- 30-
нового вектора в кодовую книгу происходит только в том случае, если оно обеспечивает уменьшение суммарного значения J .
Во-вторых, при разделении вектора шаг производится в случайном направлении,
т.е.: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x = (x0 , x1 |
ì |
+ |
= x + δ = (x0 |
+ δ0 , x1 + δ1,..., xn−1 + δn−1 ) |
|
|
|||||||||||||||||||
,..., xn−1 ) Þ íïx |
|
, |
(13) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ïx− |
= x - δ = (x |
0 |
-δ |
0 |
, x -δ |
,..., x |
n−1 |
-δ |
n−1 |
) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
1 1 |
|
|
|
|
|
|
||||
где δ = ε |
|
|
|
|
s |
|
|
|
|
, sk ~ N (mk ,σk ). Для простоты в программе использовались одинаковые |
|||||||||||||||
|
|
|
|
s |
|
|
|
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параметры |
|
|
для каждой координаты: |
|
m0 |
|
= m1 = ... = mn−1 |
и |
|
σ0 = σ1 = ... = σn−1 . |
Таким |
||||||||||||||
образом, в отличие от стандартного алгоритма «разделения» данный алгоритм не выделяет какое-то фиксированное направление, в котором всегда происходит расщепление вектора, что дополнительно улучшает результат.
Приведем полную схему алгоритма, описанного выше. Пусть в начале работы задана последовательность обучающих векторов {am}Mm=−01 , желаемая длина кодовой книги Lmax , а
также максимальное количество итераций qmax (для предотвращения зацикливания в случае, если долгое время не удается провести успешное «разделение» ни одного вектора).
Шаг 0. Инициализация.
|
1 |
M −1 |
|
Задать начальную кодовую книгу C = {c0}, где c0 = |
åam , |
||
|
|||
|
M m=0 |
||
установить длину кодовой книги L = 1, установить J1 = +∞ ,
установить номер очередного вектора, подлежащего «разделению» j = 0 .
Шаг 1. Скопировать текущую кодовую книгу: C0 = C .
Положить среднюю ошибку E0 = +¥ , установить счетчик итераций i = 0 , установить счетчик зацикливания q = 0 .
Шаг 2. Провести «разделение» вектора сij на два вектора в соответствии с формулой
(13). Удалить вектор сij из кодовой книги, а векторы cij+ и cij− добавить в ее конец.
Увеличить длину кодовой книги: L = L +1.
