
- •1.1. Основные понятия
- •1.2. Понятие контекстного кодирования
- •1.3. Обзор методов цифровой видеокомпрессии
- •1.3.1. Общие идеи
- •1.3.2. Motion JPEG
- •1.3.4. MPEG-2
- •1.3.5. MPEG-4
- •1.4. Методы компенсации движения
- •1.4.1. Общие идеи
- •1.4.2. Полный перебор
- •1.4.3. Перебор соседних блоков
- •1.4.4. Трехшаговый алгоритм Koga и др.
- •1.4.5. Алгоритмы diamond search и cross-diamond search
- •1.5. Выводы
- •2. Алгоритм видеокомпрессии
- •2.1. Общая схема
- •2.2. Компенсация движения
- •2.3. Кодирование векторов движения
- •2.4. Уточняющее изображение
- •2.5. Кодирование цветоразностной информации
- •2.6. Вывод информации в битовый поток
- •3. Тестирование алгоритма
- •4. Оптимизация вычислений

1. Сжатие статических изображений и видеосигналов
стандарт практически полностью заменит MPEG-2, позволяя передавать HDTVвидеосигнал с приемлемым битрейтом.
1.4. Методы компенсации движения
1.4.1. Общие идеи
Существуют различные методы, учитывающие временную зависимость между соседними видеокадрами. Большинство из них работает с разбиением кадра на блоки в пространственной области, но существуют и алгоритмы, действующие в области вейвлет-преобразования [12]; специально для сжатия видео были разработаны также трехмерные преобразования [13]. В данной работе проведен обзор только алгоритмов первого типа как наиболее популярных.
Простейшим способом учета временной зависимости является попиксельная разность кадров. Этот метод эффективен для неподвижных сцен, но если в кадре есть какое-то движение, то его недостатки сразу же проявляются (см. рис. 1в). В зависимости от текстуры находящегося в кадре объекта разность может увеличиться весьма значительно, причем неблагоприятным для алгоритма образом (может содержать много резких, высокочастотных переходов яркости). Поэтому все современные алгоритмы сжимают не просто попиксельную разность двух последовательных кадров, а так называемый скомпенсированный кадр (см. рис. 1г). Для вычисления скомпенсированного кадра необходимо сначала преобразовать один из соседних уже сжатых кадров следующим образом: объекты в кадре (в идеале – все) должны быть перемещены и/или трансформированы так, чтобы этот измененный кадр был как можно более близок в некоторой метрике к текущему кодируемому кадру. Разность преобразованного и текущего кадра называется скомпенсированным кадром и подвергается сжатию. То есть следующий кадр можно получить, зная соседний кадр (например, предыдущий), скомпенсированный кадр (обычно кодируются только его части, несущие полезную информацию), и некоторую дополнительную информацию, которая называется информацией о движении. Эффективность такого подхода по сравнению с вычислением попиксельной разности наглядно показана на рис. 1, на котором видно, что скомпенсированный кадр не несет почти никакой информации, а значит, может быть закодирован с очень высокой степенью сжатия.
15

1. Сжатие статических изображений и видеосигналов
Рис. 1. Соседние кадры (а) и (б), их попиксельная разность (в) и скомпенсированный кадр (г)
Вычислительная мощность современных компьютеров пока не позволяет использовать сложные математические преобразования над потоком кадров в реальном времени, поэтому используются вычислительно эффективные, а значит, относительно простые методы. Обычно ограничиваются поиском перемещенных блоков между текущим и предыдущим кадром.
Задачу поиска перемещенных блоков изображения сформулируем следующим образом: для заданного (m,n)-блока Bim,n i-ого кадра требуется найти в предыдущем кадре такой (y, x)-блок Biy,x−1 , чтобы
D(Bim,n ,Biy−,1x )<ε , |
(2) |
|
где D – отклонение (т.е. некоторым образом введенное расстояние в пространстве |
||
матриц размерности N1×N2), ε – заданная точность. Если неравенство выполняется, |
||
то можно считать, что блок Bim,n |
– это перемещенный фрагмент Biy,x−1 предыдущего |
|
кадра. Существуют различные |
алгоритмы поиска перемещенных |
блоков. В |
16

1. Сжатие статических изображений и видеосигналов
пп. 1.4.2-1.4.4 процитирован из [1] краткий обзор таких алгоритмов, дополненный двумя современными методами.
1.4.2. Полный перебор
Просматриваются все блоки Biy,x−1 , и находится блок Biy−*1,x* :
D(Bim,n ,Bi−*1 |
* )= min D(Bim,n ,Biy−,1x ), |
y ,x |
Ω |
|
Ω= 0 ≤ x ≤ M2 − N2.0 ≤ y ≤ M1 − N1
Если D(Bim,n ,Biy−*1,x* )<ε , то полагаем найденный блок Biy−*1,x* решением задачи
поиска перемещенного блока, иначе считаем, что данная задача для блока Bim,n не
имеет решения.
1.4.3. Перебор соседних блоков
Поскольку наиболее вероятными являются небольшие межкадровые перемещения блоков видеоизображения, для ускорения процедуры поиска при полном переборе можно сузить область поиска блоков Biy,x−1 , ограничившись
значениями x и y, ближайшими к n и m.
Для ускорения обработки поиск можно останавливать на первом же блоке,
который удовлетворяет условию (2), а последовательность просмотра блоков Biy,x−1
выбирать так, чтобы в первую очередь проверялись блоки с меньшим перемещением.
Очевидно, что первый из приведенных алгоритмов поиска находит наилучшее
приближение для кодируемого блока Bim,n , и если в предыдущем кадре существует
блок Biy,x−1 , удовлетворяющий условию (2), то такой блок будет всегда найден.
Однако осуществление полного перебора блоков предыдущего кадра представляет собой вычислительно громоздкую процедуру, в большинстве случаев непригодную для практического применения. Ускорение перебора за счет сокращения области поиска, имеющее место во втором алгоритме, в качестве оборотной стороны влечет за собой и уменьшение количества найденных перемещенных блоков.
17
1. Сжатие статических изображений и видеосигналов
Альтернативой методам перебора являются методы направленного многошагового поиска. Не претендуя на абсолютные результаты, которые достигаются полным перебором всех блоков, данные алгоритмы ставят цель расширения области поиска и, соответственно, повышения числа найденных перемещенных блоков, при сохранении числа «проб», т.е. вычисления отклонения D(Bim,n ,Biy−,1x ), на уровне,
приемлемом для практического использования алгоритмов.
1.4.4. Трехшаговый алгоритм Koga и др.
В данном алгоритме [14] поиск перемещенного блока Biy,x−1 , состоящий в
нахождении его координат ( |
y , x )= (y −m, |
x −n) относительно обрабатываемого |
|
блока Bim,n , производится итерационным уточнением координат |
( y , x ), см. |
||
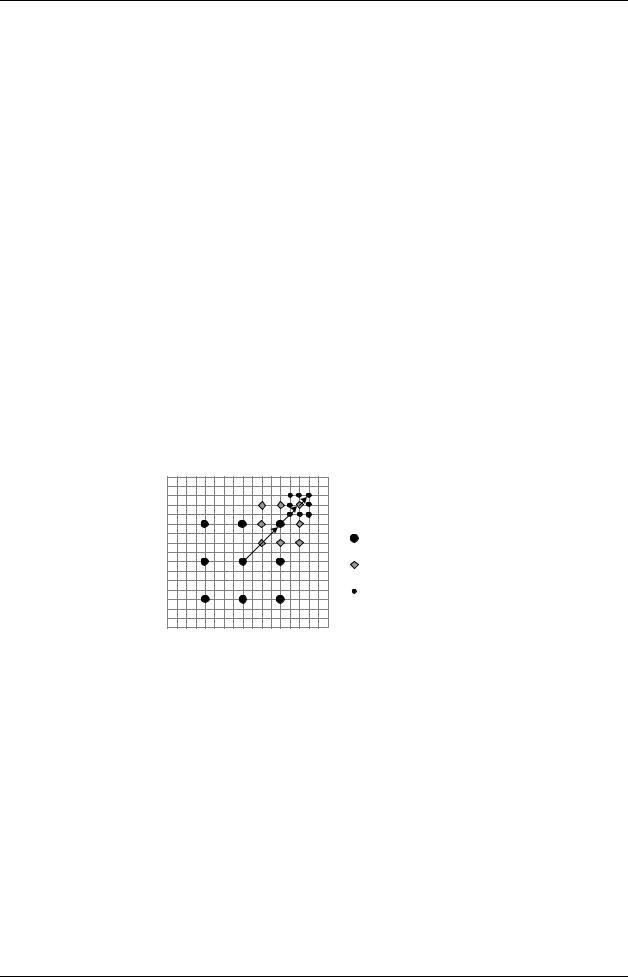
рис. 2. На первом шаге |
производится |
девять вычислений |
отклонения |
D(Bim,n ,Biy−,1x ), точка (y, x), давшая наименьшее значение отклонения, становится
начальной точкой поиска на второй итерации (шаге).
Рис. 2. Шаги алгоритма Koga и др.
На втором и третьем шагах выполняется уже по 8 вычислений отклонения. Таким образом, общее число «проб» равно 25. При этом область поиска Ω представляет собой квадрат из 225 точек.
1.4.5. Алгоритмы diamond search и cross-diamond search
Одним из самых распространенных в современных видеокодеках является алгоритм поиска перемещенных блоков под названием diamond search (DS) [15].
18
1. Сжатие статических изображений и видеосигналов
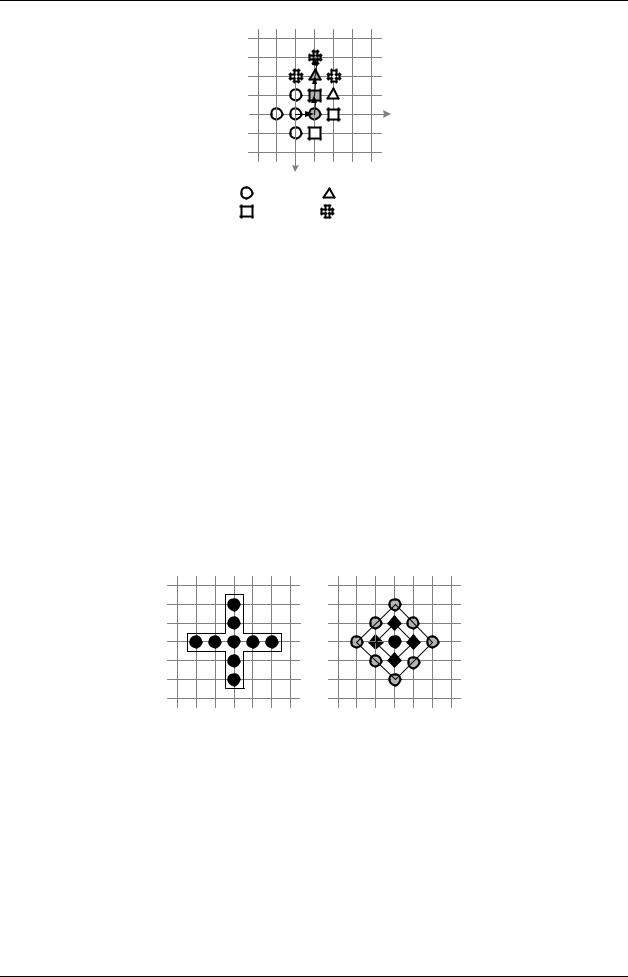
Рис. 3. Работа алгоритма diamond search
Поиск перемещенного блока начинается из точки (0, 0). На каждом шаге
вычисляется значение меры отклонения в 5 точках-соседях, образующих ромб (его можно полностью увидеть на шаге 1). Если точкой с наименьшим отклонением окажется центральная точка ромба, то поиск прекращается и найденный вектор объявляется вектором движения, в противном случае центр поиска перемещается в только что найденную точку с наименьшим отклонением и проводится новое измерение.
Усовершенствованием данного метода является алгоритм cross-diamond search (CDS) [16]. В нем используется несколько шаблонов (рис. 4) для поиска оптимального вектора движения.
Рис. 4. Шаблоны поиска алгоритма CDS: (а) крест, (б) большой и малый ромбы
Алгоритм CDS устроен несколько сложнее DS, но обеспечивает большую эффективность поиска. Примеры его работы показаны на рис. 5.
19
1. Сжатие статических изображений и видеосигналов |
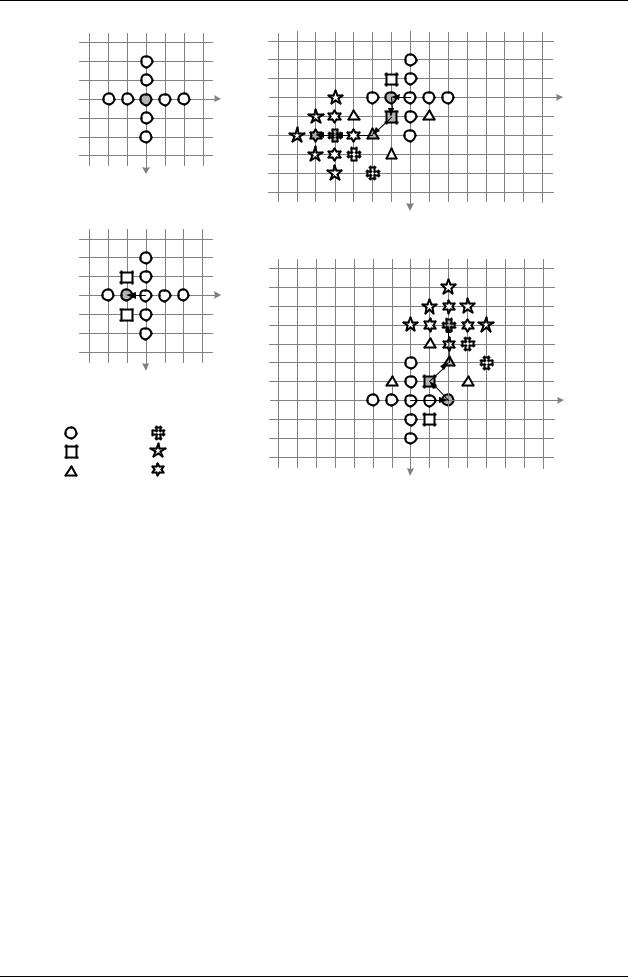
Рис. 5. Пример работы алгоритма CDS: (а) остановка на первом шаге, (б) остановка на втором шаге, (в) поиск оптимального вектора (−5; 2), (г) поиск оптимального вектора
(2; −4), при этом вектор с такими координатами вычисляется уже на 4-м шаге и далее не изменяется.
В начале работы алгоритм проводит поиск в области 5×5 пикселов по
крестообразному шаблону (рис. 4а). Он добавлен в алгоритм потому, что в этой области обычно находятся более 90% векторов движения и для них нужен более точный поиск. Если минимум отклонения достигается в центральной точке шаблона (рис. 5а), то оптимальным вектором считается нулевой вектор и работа алгоритма завершается.
На втором шаге используется шаблон «большой ромб» с центром также в точке (0, 0), причем измерения отклонения проводятся всего в двух его точках,
ближайших к точке минимума отклонения на первом шаге. Если после первого шага оптимальный вектор окажется равным (±1; 0) или (0; ±1) и после второго шага он останется на том же месте (рис. 5б), то вектор движения считается найденным и работа алгоритма завершается.
20
