Изменение матрицы линейного преобразования при изменении базиса

В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой.

Пусть ---мерное линейное пространство,и-- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть-- матрица перехода 19.1.4 а от старого базиса к новому.

        Предложение 19.1   Пусть -- линейное преобразование пространства,и-- матрицы этого преобразования в старом и новом базисе соответственно. Тогда

        Доказательство.     Пусть -- произвольный вектор пространства,-- его образ, то есть. Пустьи-- координатные столбцы векторовив старом базисе, а,-- в новом. Тогда в силу формулы (19.3). Попредложению 18.5имеем,. Подставим эти выражения в предыдущую формулу, получаем. Откуда. С другой стороны, в силу формулы (19.3) в новом базисе. Сравнивая это равенство с предыдущим, получаем.

        Определение 19.2   Две квадратных матрицы иодного порядка называютсяподобными, если существует такая невырожденная матрица , что.

Следствие 19.1   Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.

Билет №19.

Собственные значения и собственные векторы линейного оператора. Их свойства и вычисление.

Определение. Пусть A — линейный оператор, действующий в линейном пространстве Rⁿ. Число 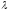называется собственным значением, аненулевой вектор 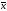изRⁿ — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением..

По теореме о связи координат образа и прообраза имеем: 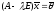, гдеE — единичная матрица, а 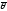— нулевой векторRⁿ .

Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы . Ненулевое решение однородной системы (система нетривиально совместна), существует тогда и только тогда, когда определитель матрицы системы равен нулю:. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения, а собственные векторы — как решения соответствующих однородных систем.

Легко видеть, что определитель — многочлен n-й степени относительно .

Определение. Уравнение 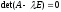называется характеристическим уравнением оператора, а многочлен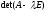— характеристическим многочленом оператора.

Примеры.

1. Нулевой оператор: , матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е. т.е. — единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространстваRⁿ.

Свойства собственных векторов

Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:

1. характеристический многочлен оператора, действующего в Rⁿ является многочленом n-й степени относительно ;

2. линейный оператор, действующий в Rⁿ, имеет не более n различных собственных значений;

3. собственные векторы оператора определяются с точностью до постоянного сомножителя; поэтому принять вычислять собственные векторы единичной длины — орты собственных векторов;

докажем, что если 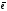— собственный вектор линейного оператора A, отвечающий собственному значению , то для любогоотличного от нуля числа вектор(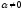)— собственный вектор оператораA, отвечающий собственному значению :;

4. корни характеристического многочлена не зависят от базиса;

5. собственные векторы, отвечающие различным собственным значениям, линейно независимы.

20.Кривые 2-го порядка

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида.