
- •1. Рассчитать удельные механические нагрузки от внешнего воздействия метеорологических факторов и сил тяжести на провода и тросы с учетом их высоты крепления на промежуточной опоре.
- •4. Составить для проводов монтажную таблицу и построить монтажные графики, соответствующие характерным длинам промежуточных пролетов линии.
- •6. Выбрать тип и количество подвесных стеклянных тарельчатых изоляторов для крепления проводов к промежуточным и анкерным опорам.
c
Московский Энергетический институт
(Технический Университет)
Кафедра ЭЭС
РАСЧЕТНОЕ ЗАДАНИЕ
по дисциплине «Конструкция воздушных линий электропередач»
МЕХАНИЧЕСКИЙ РАСЧЕТ ПРОВОДОВ, ТРОСОВ И ИЗОЛЯТОРОВ ВОЗДУШНЫХ ЛИНИЙ
Вариант № 38
Студент: Пономаренко В.
Преподаватель: Платонова И.А.
Группа: Э-06-07
Москва 2011 г.
ИСХОДНЫЕ ДАННЫЕ
Провод:
Марка провода: АС 240/39
Число проволок в алюминиевой части nА = 26 c øА = 3,4 мм в 2 пов. ([1] т.3)
Число проволок в стальной части nС = 7 c øС = 2,65 мм в 1 повив ([1] табл.3)
Действительное значение сечения проводника: FА = 236 мм2.
Действительное значение сечения стального сердечника: FC = 38,6 мм2.
Действительное значение сечения провода: FП = 274,6 мм2.
Диаметр провода: dп = 21,6 мм.
Диаметр стального сердечника: dС = 8 мм ([1] приложение 1табл.4)
Удельная масса провода (без смазки): M = 952 кг/км.
Соотношение
сечений:
 – норм. конструкция провода
– норм. конструкция провода
Допустимое напряжение при наибольшей нагрузке и низшей температуре:
 ([2]
табл.2.5.7)
([2]
табл.2.5.7)
Допустимое напряжение при среднегодовой температуре:
 ([2]
табл.2.5.7)
([2]
табл.2.5.7)
Модуль
упругости:
 ([2]
табл.2.5.8)
([2]
табл.2.5.8)
Температурный
коэффициент линейного удлинения:
 ([2]
табл.2.5.8)
([2]
табл.2.5.8)
Распределение проволок по повивам:





Рис.1. Поперечное сечение провода АС 240/39.
Наименьшее
расстояние от проводов ВЛ до поверхности
земли для ВЛ 220 кВ на ненаселенной
местности:
 .
([2] табл.2.5.20)
.
([2] табл.2.5.20)
Трос:
Марка троса: ТК-11
Номинальное сечение троса Fтном = 70 мм2
Диаметр троса dт = 11,0 мм
Расчётное сечение троса Fт = 72,58 мм2
Масса троса Mт = 623 кг/км
Допустимое
напряжение при наибольшей нагрузке и
низшей температуре:
 [2]
табл.2.5.8)
[2]
табл.2.5.8)
Допустимое напряжение при среднегодовой температуре:
 ([2]
табл.2.5.8)
([2]
табл.2.5.8)
Модуль
упругости:
 ([2]
табл.2.5.8)
([2]
табл.2.5.8)
Температурный
коэффициент линейного удлинения:
 ([2]
табл.2.5.8)
([2]
табл.2.5.8)
Опора:
Исходя
из следующих данных: провод АС 240/39,
 (II
ветровой район),
(II
ветровой район),
 (IV
гололедный район),
(IV
гололедный район),
 ,
материал опор – сталь, то по [3] табл.8.21выбирается
промежуточная двухцепная свободностоящая
стальная опора П220-2 и характеризуется
конструктивными размерами, указанными
на рис.2. Высота поддерживающей гирлянды
изоляторов равна 2,3 м для ВЛ 220 кВ
[4].
,
материал опор – сталь, то по [3] табл.8.21выбирается
промежуточная двухцепная свободностоящая
стальная опора П220-2 и характеризуется
конструктивными размерами, указанными
на рис.2. Высота поддерживающей гирлянды
изоляторов равна 2,3 м для ВЛ 220 кВ
[4].

Рис.2. Промежуточная двухцепная свободностоящая стальная опора П220-2
1. Рассчитать удельные механические нагрузки от внешнего воздействия метеорологических факторов и сил тяжести на провода и тросы с учетом их высоты крепления на промежуточной опоре.
1.1. Постоянно действующая удельная нагрузка от собственной массы провода (троса)

Провод:
 .
.
Трос:
 .
.
1.2. Временно действующая нагрузка от массы гололедных отложений Провод.
 Н/(м∙мм2),
Н/(м∙мм2),
Здесь b=bн kdb∙khb - расчетная толщина стенки гололедного цилиндра на проводе, причем:
bн=25 мм – нормативная толщина стенки гололеда;
kdb – поправочный коэффициент на толщину стенки гололеда, учитывающий отличие диаметра провода от 10 мм;
khb – поправочный коэффициент на толщину стенки гололеда, учитывающий отличие высоты расположения приведенного центра тяжести системы проводов h*цт от 14,3 метров (если h*цт<14,3 м, то khb=1).
Поправочные коэффициенты рассчитываются по следующим аппроксимирующим формулам:
 ;
;
Для определения khb необходимо найти высоту расположения приведенного центра тяжести системы проводов.
Расчет допустимой стрелы провеса:
[f] = hт − hг – λ, где hт = 22,5 м – высота от нижней траверсы до земли.
Таким образом:
[f] =22,5-7-2,3=13,2 м.
Высота центра тяжести нижнего провода:

Высота приведенного центра тяжести:
h*цт
=(3 11,4
+2
11,4
+2 6,5+6,5)/3
= 17,9м > 14,3 м,
следовательно
6,5+6,5)/3
= 17,9м > 14,3 м,
следовательно
khb
=
 = 1,1
= 1,1
Расчётная толщина стенки ледяного цилиндра на проводе:
b = bн kdb∙khb = 25∙0,855∙1,1 = 23,51 мм2.

Трос:
 Н/(м∙мм2),
Н/(м∙мм2),
Расчет поправочных коэффициентов:
Т.к. dт > 10 мм, то:

Для определения khbТ необходимо найти высоту расположения центра тяжести троса.
Допустимая стрела провеса троса принимается такой же, как и допустимая стрела провеса провода: [fт] = [fп] = [f] = 13,2 м.
Высота опоры: Hоп = 41 м

bТ = bн kdbТ∙khbТ = 25∙0,98∙1,384 = 33,91 мм2.
 Н/(м∙мм2).
Н/(м∙мм2).
1.3. Суммарная вертикальная удельная механическая нагрузка от собственной массы провода (троса) и массы гололедных отложений.
 Н/(м∙мм2).
Н/(м∙мм2).
Провод:
 Н/(м∙мм2).
Н/(м∙мм2).
Трос:
 Н/(м∙мм2).
Н/(м∙мм2).
1.4. Временно действующая горизонтальная нагрузка от давления ветра на провод (трос), свободный от гололеда.
 Н/(м∙мм2)
Н/(м∙мм2)
Провод.
Нормативное ветровое давление WН = 500 Н/м2 : 270 Н/м2 < WН < 745 Н/м2
Следовательно,
коэффициент, учитывающий
неравномерность распределения ветрового
давления по пролету: .
.
Аэродинамический коэффициент лобового сопротивления для проводов, свободных от гололеда по [2]:
Cx = 1,1 (так как dп = 21,6 > 20 мм).
Поправочный коэффициент на ветровое давление в зависимости от высоты:
 =
=
Принимаем вектор скорости ветра направленным перпендикулярно проводам, тогда sinφ = 1:
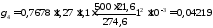 Н/(м∙мм2).
Н/(м∙мм2).
Трос:
 Н/(м∙мм2)
Н/(м∙мм2)
 W
= 0,7678 (из расчета провода)
W
= 0,7678 (из расчета провода)
Аэродинамический коэффициент лобового сопротивления для троса, свободного от гололеда по [2]: CxТ = 1,2, так какdт = 11 < 20 мм.
Поправочный
коэффициент на высоту троса
 ,
(т.к.h*цт
>14,3
м)
,
(т.к.h*цт
>14,3
м)
Принимаем, что вектор скорости ветра направлен перпендикулярно оси троса, тогда sinφ = 1 и удельная нагрузка равна:
 Н/(м∙мм2).
Н/(м∙мм2).
1.5. Временно действующая горизонтальная нагрузка от давления ветра на провод (трос), покрытый гололедом.
 Н/(м∙мм2).
Н/(м∙мм2).
Нормативное ветровое давление при гололеде с повторяемостью 1 раз в 25 лет ([2]):

Так
как
 <
270Н,
то
коэффициент
<
270Н,
то
коэффициент
 =
1
=
1
Аэродинамический коэффициент лобового сопротивления для проводов и тросов, покрытых гололедом ([2]):
CxГ = 1,2
Провод:
 Н/(м∙мм2).
Н/(м∙мм2).
Трос:
 Н/(м∙мм2).
Н/(м∙мм2).
1.6 Суммарная наибольшая нагрузка на провод (трос) в отсутствие гололеда.
 Н/(м∙мм2).
Н/(м∙мм2).
Провод:
 Н/(м∙мм2).
Н/(м∙мм2).
Трос:
 Н/(м∙мм2).
Н/(м∙мм2).
1.7. Суммарная наибольшая нагрузка на провод (трос), покрытый гололедом.
 Н/(м∙мм2).
Н/(м∙мм2).
Провод:
 Н/(м∙мм2).
Н/(м∙мм2).
Трос:

Из нагрузок γ6 и γ7 наибольшей для провода является γ7 = 0,149 Н/(м∙мм2).
Для троса наибольшей является γ7Т = 0,714 Н/(м∙мм2).
2. Построить зависимости среднеэксплуатационного напряжения в проводе от длины пролета, определить значения критических пролетов и выбрать определяющее по прочности провода нормативное сочетание климатических условий, основываясь на нормируемых значениях допустимых напряжений и эквивалентных физико-математических параметрах.
Уравнение состояния провода в форме записи относительно напряжений:

Расчет
выполняется для анкерных пролетов
различной длины, поэтому
 ,
следовательно, слагаемое
,
следовательно, слагаемое
 в уравнении состояния провода отсутствует.
в уравнении состояния провода отсутствует.
2.1. В качестве исходных условий принимается нормативное сочетание климатических условий, соответствующее наибольшей механической нагрузке.
Исходные
условия – нормативное сочетание
климатических условий (НСКУ) при
 :
:



Искомые условия – среднеэксплуатационные:



Уравнение состояния провода в этом случае имеет следующий вид:

Уравнение состояния провода через коэффициенты А и В:



При
 уравнение состояния становится
вырожденным:
уравнение состояния становится
вырожденным:

При
 уравнение состояния также становится
вырожденным:
уравнение состояния также становится
вырожденным:

Расчет среднеэксплуатационных напряжений для каждой длины пролета выполняется итерационным методом Ньютона:

Где
k
– номер текущей итерации. Расчет ведется
до достижения заданной точности ξ =0,1
 ,
т.е. |
,
т.е. | 0,1
0,1 .
.
При
 :
:
В качестве начального приближения среднеэксплуатационного напряжения принимается:








Расчет для остальных длин пролетов сведен в таблицу 2.1.
Таблица 2.1.
|
|
|
|
|
|
|
|
|
|
|
100 |
69,37 |
39740 |
128,6 |
89,18 |
78,92 |
76,37 |
76,21 |
76,21 |
|
200 |
-56,26 |
158960 |
76,21 |
52,73 |
42,64 |
40,61 |
40,53 |
|
|
300 |
-265,63 |
357660 |
40,53 |
35,04 |
34,52 |
34,52 |
|
|
|
400 |
-558,74 |
635840 |
34,52 |
32,83 |
32,79 |
|
|
|
|
500 |
-935,61 |
993500 |
32,79 |
32,05 |
32,04 |
|
|
|
|
600 |
-1396,2 |
1430640 |
32,04 |
31,66 |
31,65 |
|
|
|
2.2. В качестве исходных условий принимается нормативное сочетание климатических условий, соответствующее низшей температуре.
Исходные
условия – нормативное сочетание
климатических условий при
 :
:



Искомые условия – среднеэксплуатационные:



Уравнение состояния провода принимает вид:

Коэффициенты:


При
 уравнение состояния становится
вырожденным:
уравнение состояния становится
вырожденным:

При
 уравнение состояния также становится
вырожденным:
уравнение состояния также становится
вырожденным:

При
 :
:
В качестве начального приближения среднеэксплуатационного напряжения принимается:






Расчет для всех остальных длин пролетов сведен в таблицу 2.2.
Таблица 2.2.
|
|
|
|
|
|
|
|
|
100 |
61,54 |
39740 |
63,72 |
70,840 |
69,746 |
69,716 |
|
200 |
55,00 |
158960 |
69,716 |
82,365 |
80,002 |
79,900 |
|
300 |
44,10 |
357660 |
79,900 |
90,566 |
89,154 |
89,126 |
|
400 |
28,84 |
635840 |
89,126 |
97,524 |
96,764 |
96,757 |
|
500 |
9,22 |
993500 |
96,757 |
103,372 |
102,955 |
102,953 |
|
600 |
-14,76 |
1430640 |
102,953 |
108,205 |
107,968 |
107,968 |
2.3. Зависимости среднеэксплуатационного напряжения в проводе от длины пролета.

Рис.2.3. Зависимости среднеэксплуатационного напряжения в проводе от длины пролета.
Выбор
определяющего по прочности провода
нормативного сочетания климатических
условий (НСКУ) осуществляется по правилу
наименьших ординат кривых
 .
Согласно данному правилу, весь диапазон
длин пролетов для рассматриваемого
случая делится на два интервала:
.
Согласно данному правилу, весь диапазон
длин пролетов для рассматриваемого
случая делится на два интервала:
 и
и .
Соответствующие этим интервалам участки
кривых выделены штриховкой.
.
Соответствующие этим интервалам участки
кривых выделены штриховкой.
2.4. Выбор определяющего по прочности провода НСКУ по методу критических пролетов.
При
 и исходных условиях, соответствующих
и исходных условиях, соответствующих
 ,
рассчитывается среднеэксплуатационное
напряжение в проводе:
,
рассчитывается среднеэксплуатационное
напряжение в проводе:

 ,
следовательно значение
,
следовательно значение
 является действительным. Расчет значения
является действительным. Расчет значения .
.

При
 и исходных условиях, соответствующих
и исходных условиях, соответствующих
 ,
рассчитывается среднеэксплуатационное
напряжение в проводе:
,
рассчитывается среднеэксплуатационное
напряжение в проводе:

 ,
следовательно значение
,
следовательно значение
 является действительным. Расчет значения
является действительным. Расчет значения :
:

Так
как
 ,
то
,
то необходимо рассчитать.
необходимо рассчитать.
Расчет
значения
 :
:

Имеем
 .
.
2.5. Выводы об определяющих по прочности провода НСКУ.
На основании построенных зависимостей, видно:
При
 определяющим по прочности провода
является нормативное сочетание
климатических условий при
определяющим по прочности провода
является нормативное сочетание
климатических условий при .
.
При
 определяющим по прочности провода
является нормативное сочетание
климатических условий при
определяющим по прочности провода
является нормативное сочетание
климатических условий при .
.
По
[3] табл.8.23 для двухцепной свободностоящей
стальной опоры П220-2 для IV
района по гололеду верифицированная
длина пролета
 ,
таким образом, для данных воздушных
линий определяющим по прочности провода
является нормативное сочетание
климатических условий при
,
таким образом, для данных воздушных
линий определяющим по прочности провода
является нормативное сочетание
климатических условий при .
.
3. Вычислив критическую температуру, установить нормативное сочетание климатических условий наибольшего провисания проводов и рассчитать габаритный пролет; построить шаблон для расстановки опор по продольному профилю трассы ВЛ с соблюдением масштабов: по вертикали – 1:500, по горизонтали – 1:5000.
3.1. Вычисление приблизительного значения критической температуры воздуха по оценочной формуле.
Оценочная формула:

Производится сравнение критической температуры с высшей:

Из
сравнения следует, что
 ,
а, следовательно, стрела провеса провода
в любом пролете будет больше при
нормативной толщине стенки гололеда
без ветра, то есть под действиемсуммарной
вертикальной нагрузки от собственной
массы провода и массы гололедных
отложений
,
а, следовательно, стрела провеса провода
в любом пролете будет больше при
нормативной толщине стенки гололеда
без ветра, то есть под действиемсуммарной
вертикальной нагрузки от собственной
массы провода и массы гололедных
отложений
 .
.
Таким образом, габаритными климатическими условиями являются гололедные без ветра.
3.2. Расчет габаритного пролета.
Из
пункта 2 известно, что при выборе
определяющего по прочности нормативного
сочетания климатических условий следует
ориентироваться на значение
 :
:
При
 определяющим по прочности провода
является нормативное сочетание
климатических условий при
определяющим по прочности провода
является нормативное сочетание
климатических условий при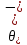 .
.
При
 определяющим по прочности провода
является нормативное сочетание
климатических условий при
определяющим по прочности провода
является нормативное сочетание
климатических условий при .
.
Так
как точно не известно, к какому из двух
интервалов принадлежит значение
 ,
то расчет выполняется в соответствии
с нижеследующим алгоритмом.
,
то расчет выполняется в соответствии
с нижеследующим алгоритмом.
3.2.1.
Предположим, что
 и зададимся исходными условиями,
соответствующими
и зададимся исходными условиями,
соответствующими .
.
Исходные условия:



Искомые условия:


Величина габаритного пролета определяется из уравнения:

Уравнение состояния провода через коэффициенты:




Решая биквадратное уравнение, получаем формулу для нахождения величины габаритного пролета:

Из
сравнения
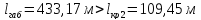 ,
видно, что значение
,
видно, что значение попадает в интервал длин пролетов
попадает в интервал длин пролетов ,
для которого определяющим по прочности
провода является нормативное сочетание
климатических условий при
,
для которого определяющим по прочности
провода является нормативное сочетание
климатических условий при ,
что не соответствует исходным условиям,
принятым при расчете
,
что не соответствует исходным условиям,
принятым при расчете .
Следовательно, первая проверка не
выполняется, необходимо задаться другими
исходными условиями и выполнить расчет
еще раз.
.
Следовательно, первая проверка не
выполняется, необходимо задаться другими
исходными условиями и выполнить расчет
еще раз.
3.2.2.
Предположим, что
 и зададимся исходными условиями,
соответствующими
и зададимся исходными условиями,
соответствующими .
.
Исходные условия:



Искомые условия:


Величина габаритного пролета определяется из уравнения:

Уравнение состояния провода через коэффициенты:




Решая биквадратное уравнение, получаем формулу для нахождения величины габаритного пролета:

 ,
следовательно, определяющее по прочности
провода нормативное сочетание
климатических условий для
,
следовательно, определяющее по прочности
провода нормативное сочетание
климатических условий для
 совпадает с исходными условиями. Первая
проверка выполняется.
совпадает с исходными условиями. Первая
проверка выполняется.
3.2.3. Определение напряжения в низшей точке провода в габаритном пролете при габаритных климатических условиях.
Уравнение состояния провода:

Уравнение состояния провода через коэффициенты:



Расчет ведется по итерационному методу Ньютона:

Расчет
выполняется до заданной точности
 .
.
В качестве начального приближения принимается значение допустимого напряжения при наибольшей нагрузке:




 ,
следовательно, начальное приближение
выбрано верно, и напряжение в низшей
точке провода в габаритном пролете при
габаритных климатических условиях
определено правильно.
,
следовательно, начальное приближение
выбрано верно, и напряжение в низшей
точке провода в габаритном пролете при
габаритных климатических условиях
определено правильно.
3.2.4. Вычисление габаритной стрелы провеса.

3.2.5. Проверка правильности расчета габаритного пролета.
 ,
следовательно, расчет габаритного
пролета выполнен верно.
,
следовательно, расчет габаритного
пролета выполнен верно.
3.2.6. Определение точного значения критической температуры воздуха.

Погрешность при расчете критической температуры по оценочной формуле:
Δ , следовательно, можно сделать вывод,
что оценочная формула работает правильно.
, следовательно, можно сделать вывод,
что оценочная формула работает правильно.
3.3. Построение расстановочного шаблона.
Шаблон строится на основании расчета ординат кривой наибольшего провисания провода (т.е. при габаритных климатических условиях).
Значение
абсциссы рассматривается в диапазоне
 :
:


Коэффициент шаблона:

Уравнение кривой наибольшего провисания:

Уравнение габаритной кривой:

Где

 монтажный запас.
монтажный запас.
Уравнение земляной кривой:

При
 :
:



Результаты расчета остальных ординат сведены в таблицу 3.3.
Таблица 3.3.
|
|
0 |
50 |
100 |
150 |
155,245 |
200 |
232,87 |
|
|
0 |
1,37 |
5,477 |
12,32 |
13,2 |
21,91 |
29,7 |
|
|
-7,3 |
-5,93 |
-1,823 |
5,02 |
5,9 |
14,61 |
22,4 |
|
|
-20,2 |
-18,83 |
-14,723 |
-7,88 |
-7,0 |
1,71 |
9,5 |
|
|
0 |
1 |
2 |
3 |
3,1 |
4 |
4,66 |
|
|
0 |
0,274 |
1,1 |
2,464 |
2,64 |
4,382 |
5,94 |
|
|
-1,46 |
-1,186 |
-0,365 |
1,004 |
1,18 |
2,922 |
4,48 |
|
|
-4,04 |
-3,766 |
-2,945 |
-1,576 |
-1,4 |
0,342 |
1,9 |
При расстановке опор следует также учитывать, что длина пролета не должна превышать величины, допустимой по весовым и ветровым нагрузкам, на которые рассчитаны промежуточные опоры данного типа:

Принимается допущение, что:

Расстановочный
шаблон с учетом ограничения
 представлен на рис.3.3.
представлен на рис.3.3.
























