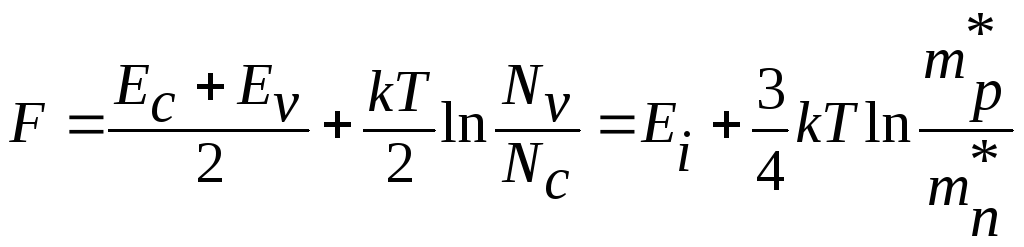Лекция 3 микроэлектроника

2.2.1 Заполнение электронами и дырками зон невырожденного полупроводника

Вероятность заполнения энергетического уровня для частицы с полуцелым спином (фермионов), то есть вероятность нахождения электрона на уровне с энергией E, определяется статистикой Ферми-Дирака (1.18)

,

(2.4)

где k – постоянная Больцмана, F – энергия Ферми.

,	(1.19)
б
Рис. 1.7

Для невырожденного полупроводника E-F»kT, »1, тогда можно применить статистику Максвелла-Больцмана:

,

(2.4)

Для того чтобы рассчитать концентрацию всех свободных электронов, т.е. концентрацию электронов в зоне проводимости, необходимо проинтегрировать по всей зоне проводимости, согласно (1.19). Поскольку функция Больцмана – очень быстро спадающая экспонента, при интегрировании по зоне в качестве верхнего предела использована ∞:

,

(2.6)

где N_с – эффективная плотность состояний в зоне проводимости или плотность квантовых состояний у дна зоны проводимости в свою зависит от температуры.

,

(2.8)

Если подставить численные значения универсальных констант, то получим:

,

(2.10)

В частности для кремния:

,

Функция распределения Ферми-Дирака для дырок имеет вид:

,

(2.5)

Функция распределения Максвелла-Больцмана для дырок

.

(2.5)

Для расчета общего количества свободных дырок выполним интегрирование по валентной зоне:

(2.7)

Эффективные плотности состояний для валентной зоны:

(2.9)

Для кремния

Значения эффективной плотности состояний для основных полупроводниковых материалов при комнатной температуре представлены в следующей таблице.

Свойство	Ge	Si	GaAs
, см-3	1,02ּ1019	2,8ּ1019	4,7ּ1017
, см-3	6,1ּ1018	1,0ּ1019	7,0ּ1018

Графически концентрации электронов и дырок можно определить согласно рис. 2.7.

2.2 Положение уровня Ферми и расчет концентрации носителей

Уровень Ферми - основной параметр статистического распределения электронов и дырок. В расчетах для определения положения уровня Ферми, как правило, используют условие электронейтральности.

Для собственного полупроводника n=p.

(2.13)

После логарифмирования (2.13) сравнительно просто рассчитывается значение уровня Ферми:

(2.14)

Из выражения (2.14) следует, что при температуре абсолютного нуля уровень Ферми для собственного полупроводника располагается посередине запрещенной зоны: .

Для собственного полупроводника вводится понятие собственной концентрации с помощью условия n_i² = np. Откуда:

	(2.15)
	(2.16)

При расчете собственной концентрации необходимо учитывать зависимость ширины запрещенной зоны от температуры (1.17). Собственная концентрация является важным характеристическим параметром материала, поскольку для заданной температуры n_i² – величина постоянная не только для собственных, но и для легированных материалов (она не зависит от положения уровня Ферми). Значения собственной концентрации для основных полупроводниковых материалов представлены в таблице.

	Ge	Si	GaAs
ni, см-3	2,5ּ1013	1,6ּ1010	1,1ּ107

На рис. 2.8 для Si, Ge, GaAs приведены зависимости собственной концентрации от температуры. Из (2.15) видно, что чем больше ширина запрещенной зоны, тем больше тангенс наклона прямо).

Рис. 2.8

2.2.1 Донорный полупроводник

Ограничимся вначале областью температур, при которой имеет место лишь ионизация примесных центров, а собственная проводимость отсутствует, т.е. p₀=0. Условие электронейтральности запишется в виде:

.

(2.17)

При низких температурах концентрация свободных электронов растет только за счет ионизации примеси.

,

(2.14)

где g = 1…2 – фактор (степень) спинового вырождения для донорного полупроводника.

В невырожденном донорном полупроводнике при температуре абсолютного нуля уровень Ферми находится посередине между дном зоны проводимости и уровнем донорной примеси. При повышении температуры уровень Ферми стремится к середине запрещенной зоны.

В соответствии с положением уровня Ферми концентрация свободных электронов вначале растет по мере ионизации донорной примеси (при этом концентрация свободных дырок пренебрежимо мала).

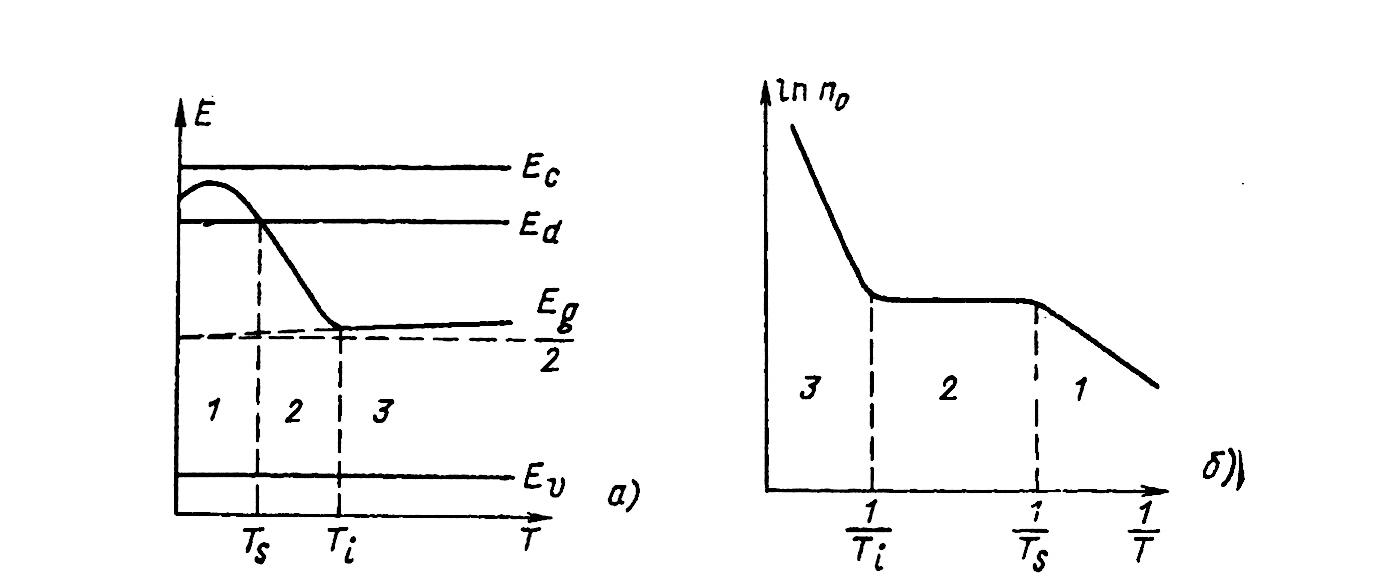
Рис. 2.9. Изменение положения уровня Ферми (а) и концентрации электронов (б) с температурой для донорного полупроводника.

На графике область слабой ионизации примеси обозначена цифрой 1 на рис. 2.9, с повышением температуры полупроводника уровень Ферми пересекает уровень донорной примеси, при этом половина донорной примеси будет ионизованна и концентрация электронов в зоне проводимости перестает зависеть от температуры.

Эта область температур носит название области истощения примеси и на рис. 2.9 обозначена цифрой 2.

Температура, при которой F=E_d носит название температуры истощения T_s

(2.16)

При дальнейшем повышении температуры увеличение концентрации электронов в зоне проводимости будет осуществляться за счет переходов электронов из валентной зоны. На рис. 2.8 область 3 соответствует области собственной проводимости. В этом случае F=E_i и

(2.18)

В области температур между T_i и T_s (при температурах, близких к комнатной) можно легко рассчитать концентрацию неосновных носителей заряда. Исходя из равенства n_i=np, , то есть увеличение концентрации электронов в результате ионизации доноров будет приводить к уменьшению концентрации дырок

Аналогичные оценки можно провести и для акцепторного полупроводника

(2.20)

В невырожденном акцепторном полупроводнике при температуре абсолютного нуля уровень Ферми лежит посередине между потолком валентной зоны и уровнем акцепторной примеси. При повышении температуры уровень Ферми также стремится к середине запрещенной зоны. В соответствии с положением уровня Ферми концентрация свободных дырок вначале растет по мере ионизации примеси (при этом концентрация свободных электронов пренебрежимо мала).

В акцепторном полупроводнике, как и в случае донорной примеси, при повышении температуры наступает область истощения, характеризующаяся полной ионизацией атомов акцепторной примеси. С дальнейшим ростом температуры уровень Ферми поднимается к середине запрещенной зоны и полупроводник ведет себя как собственный.

На рис. 2.10 представлены зависимости положения уровня Ферми от температуры для Ge n-типа (а) p-типа (б).

Рис. 2.10