3. Выходные данные

<тип> а- упорядоченный массив; ....

Замечание. Упорядочение делается принципиально в том же массиве (in situ, на месте), т.е. входной массив портится.

Чтобы не портить входные данные (это важное программистское правило, которое следует по возможности выполнять), можно использовать другой массив, например, а1, который и будет выходным. Тогда первым шагом обработки будет переписьава1, а вторым - упорядочениеа1. Здесь мы этого делать не будем.

Выходная форма должна включать исходный и упорядоченный массив с соответствующими заголовками и пояснительными текстами.

4. Аномалиине рассматриваем

5. Функциональные тестыследует составить, задав следующие варианты входных данных:

1) частично неупорядоченный массив;

2) массив, упорядоченный в обратном порядке;

3) массив, упорядоченный в требуемом порядке.

6_А. Метод включения

Пусть am- значение максимального элемента,

k- его номер.

Ищем в массиве, начиная с 1-го элемента, максимальный элемент amи его номерk. Меняем значениями 1-й иk-й элементы. Первый элемент поставлен на место.

Ищем в массиве, начиная со 2-го элемента, максимальный элемент amи его номерk. Меняем значениями 2-й иk-й элементы. Второй элемент поставлен на место.

…………………………………………….

Часть массива с 1-го по (m-1)-й элемент упорядочена.

Ищем в массиве, начиная с m-го элемента, максимальный элементamи его номерk. Меняем значениямиm-й иk-й элементы;m-й элемент поставлен на место.

……………………………………………

Часть массива с 1-го по (n-1)-й элемент упорядочена.

Ищем в массиве, начиная с m-го элемента, максимальный элемент amи его номерk. Меняем значениямиm-й иk-й (последний и предпоследний) элементы.

Массив упорядочен.

Замечание. Очевидно, тот же результат получился бы при поиске минимума и перемещении его в конец.

● Опишем метод формально.

Пусть m- номер очередного шага упорядочения (шага поиска максимума).

Дляmот 1 до (n-1) цикл

Вх.: n, a, m Вых.: [am], k

Поиск максимального элемента и его номера, начиная с m-го элемента

А1

Вх.: a, m, [am], k Вых.: a

Обмен значениями m-го иk-го элементов

А2

кц;

Задача А2 - обмен значениями элементов.

Пусть в общем случае необходимо обменять значениями две переменные cиd.

В нашем случае роль переменной cиграетa[m], роль переменнойdиграетa[k]. Значение максимума – переменнаяam– не используется.

Учитывая, что значение amвсе-таки ищется, можно его использовать и обойтись при обмене двумя операциями:

a[m]:=a[k];

a[k]:=am;

Дальнейшее тривиально и уже известно.

6_Б. Метод пузырька

Метод состоит в попарном сравнении всех элементов массива и упорядочении неупорядоченных пар. Массив просматривается до тех пор, пока не окажется полностью упорядоченным, т.е. при очередном просмотре не будет обнаружено неупорядоченных пар.

При первом просмотре максимальный элемент, постепенно перемещаясь, оказывается в начале («всплывает»), при втором – на второе место всплывает следующий по значению элемент и т.д. Отсюда – название метода.

Поясним метод на примере, используя следующие обозначения.

Пример

На данном шаге были неупорядоченные пары.

На данном шаге были неупорядоченные пары.

На данном шаге неупорядоченных пар не было. Массив упорядочен.

Кратко и четко метод может быть описан следующим образом.

Пока есть хотя бы одна пара неупорядоченных соседних элементов, повторять просмотры массива с начала до конца, упорядочивая неупорядоченные пары и фиксируя их наличие.

Пусть

лог у– переменная, фиксирующая наличие неупорядоченных пар;

истина, если массив упорядочен (неупорядоченных пар нет),

у=

ложь, в противном случае (есть хотя бы одна неупорядоченная пара).

Поскольку упорядоченность массива означает отсутствие соседних неупорядоченных пар и наоборот, переменная y по своему смыслу фиксирует одновременно и упорядоченность (или неупорядоченность) всего массива, и отсутствие (или наличие) неупорядоченных пар соседних элементов.

Схема метода

Сначала следует положить y=ложь (массив не упорядочен).

П

Вх.: n,aвых.:y

овторяем, пока массив не упорядочен (т.е.y=ложь):

Просмотр массива с упорядочением пар соседних элементов и фиксацией их наличия

А4

конец повторений

Задача А4

1. Условие. Проверить, есть ли в заданном массиве неупорядоченные пары элементов (формулировка задачи «Поиск по условию»), и упорядочить эти пары .

Другая формулировка задачи А4: проверить, упорядочен ли массив (формулировка задачи «Проверка условия»), и, если нет, упорядочить пары соседних неупорядоченных элементов .

В отличие от задач «Поиск по условию» и «Проверка условия», здесь надо просматривать весь массив.

2. Входные данные

.... n....

.... a[n] .....

3. Выходные данные

.... a[n] - измененный массив, .......

лог у– переменная, фиксирующая наличие неупорядоченных пар;

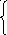истина, если массив упорядочен (неупорядоченных пар нет),

у=

ложь, в противном случае (есть хотя бы одна неупорядоченная пара).

Здесь yпринимает значения, соответствующие формулировке задачи «Проверка условия».

6. Метод

Пусть i- текущий номер элемента.

Сначала полагаем y= истина (массив упорядочен).

При просмотре массива будем сравнивать i-й иi+1-й элементы; тогдаiменяется от 1 доn-1,

Итак:

y=истина;

для i от 1 до (n-1) цикл

если <пара a[i] и a[i+1] не упорядочена> то

y:=ложь;

<упорядочить пару: поменять значениями a[i] и a[i+1] >;

кесли;

кц