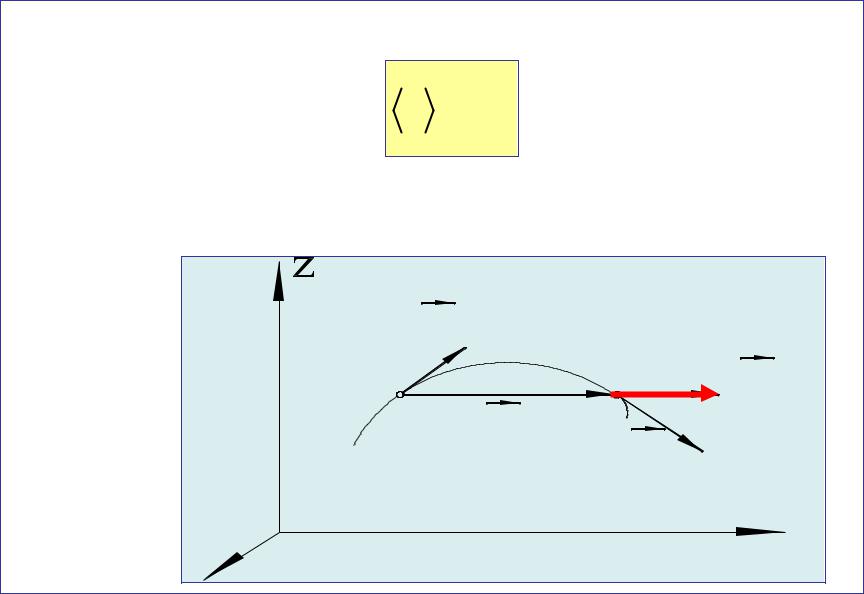
Вектор средней скорости за промежуток времени t: |
||||
- определяется как |
|
r |
|
|
|
|
v |
t |
|
- направлен вдоль вектора перемещения |
r . |
|||
|
|
V 1 |
<V > |
|
|
|
1 |
2 |
|
|
|
|
r |
2 |
|
|
|
|
|
x |
0 |
|
|
y |
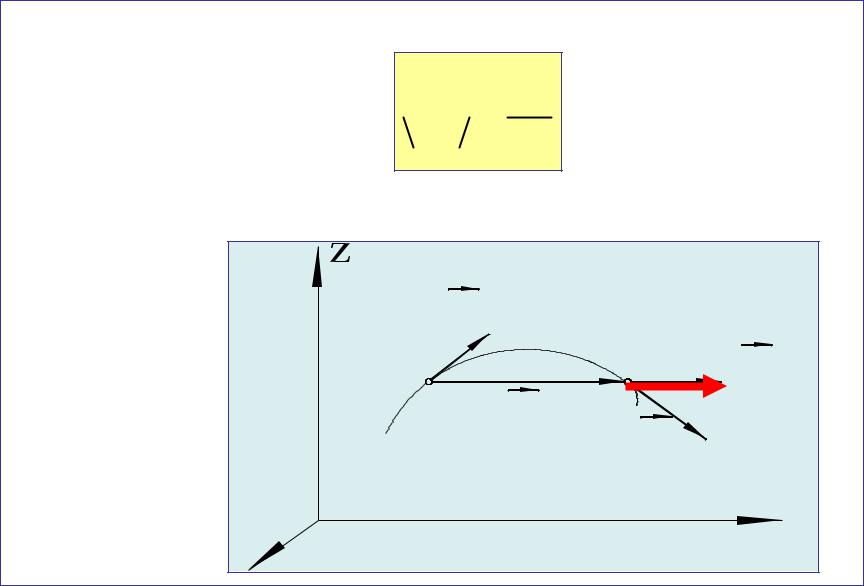
Величина модуля средней скорости равна
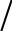v 
S
t
|
|
V 1 |
S |
<V > |
|
|
|
||
|
1 |
|
2 |
|
|
|
|
r |
2 |
|
|
|
|
|
x |
0 |
|
|
y |
При движении средняя скорость изменяет свою величину и направление.
Мгновенная скорость равна пределу, к которому стремится вектор средней скорости при неограниченном убывании промежутка времени до нуля ( t 0).
|
|
|
|
|
|
|
lim |
r |
|
dr |
|||
v |
Δt |
dt |
||||
|
Δt 0 |
|
||||
|
|
|
|
|
|
|
dr |
|
|
|
|||
v |
|
|
|
|
|
|
dt |
|
|
|
|||
Мгновенная скорость равна первой производной от радиус-вектора по времени.
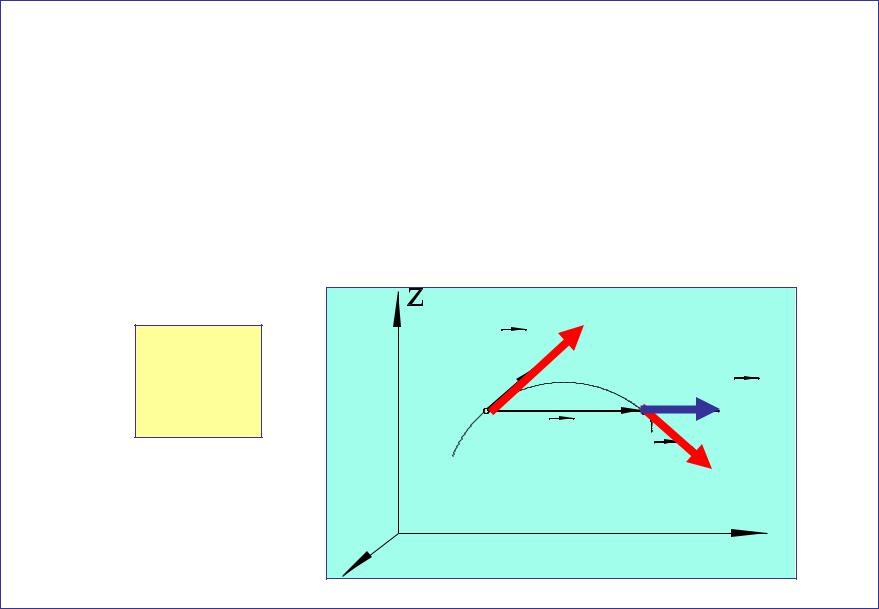
Вектор мгновенной скорости v направлен по
вектору элементарного перемещения dr , т. е. по
касательной к траектории.
Модуль мгновенной скорости равен первой производной от пути по времени:
v dS |
1 |
V 1 |
2 |
<V > |
|
|
|
||
dt |
|
r |
|
|
|
|
|
2 |
|
|
|
|
|
|
x |
0 |
|
|
y |
Проекции скорости на координатные оси равны
первым производным от координат x, y, z по времени:
vx dхdt
dy v y dt
v z dzdt
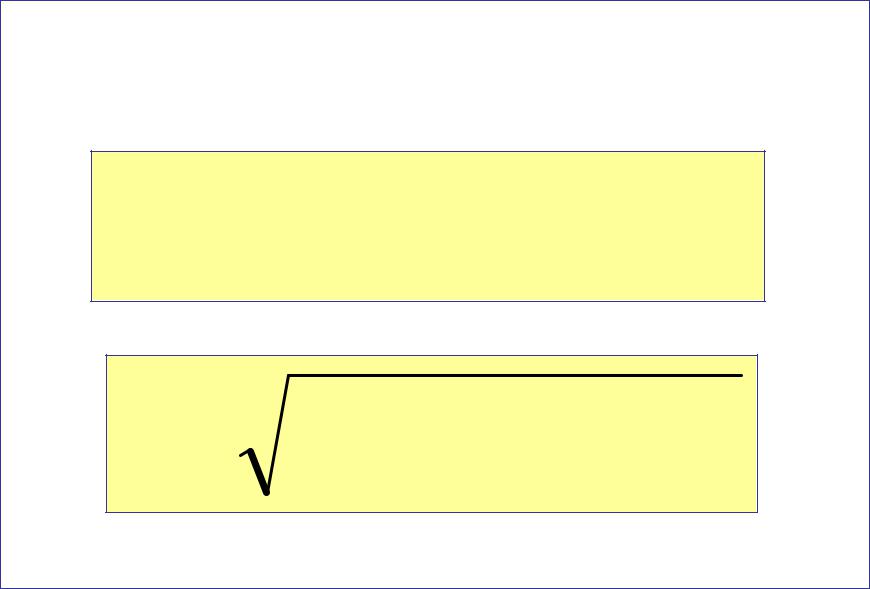
Вектор мгновенной скорости v и его модуль V |
через проекции скорости vx, vy, vz записываются как: |
|
v vx i v y j vz k |
v v 2x v 2y v z2 |
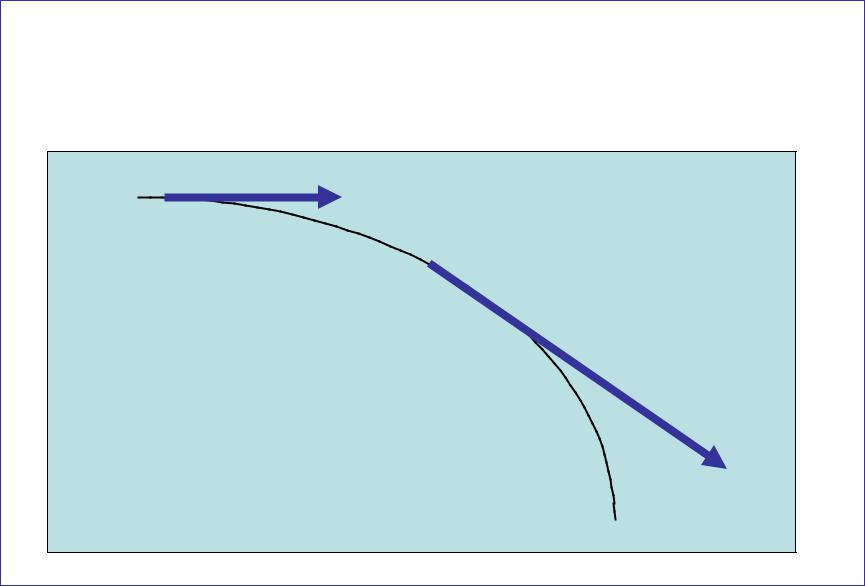
Впроцессе движения материальной точки модуль и направление скорости в общем случае изменяются.
V1 |
1 |
2 |
V2 |
Ускорение:
-равно изменению скорости за единицу времени;
-характеризует быстроту изменения скорости с течением времени;
-измеряется в м/с2;
-различают среднее и мгновенное;
-является векторной величиной.
Вектор среднего ускорения за промежуток времени t
определяется как |
|
|
|
|
|
v |
|
||
|
|
|||
|
a |
|
t |
, |
|
|
|
|
|
где |
v v2 |
v1 |
– изменение скорости за время t. |
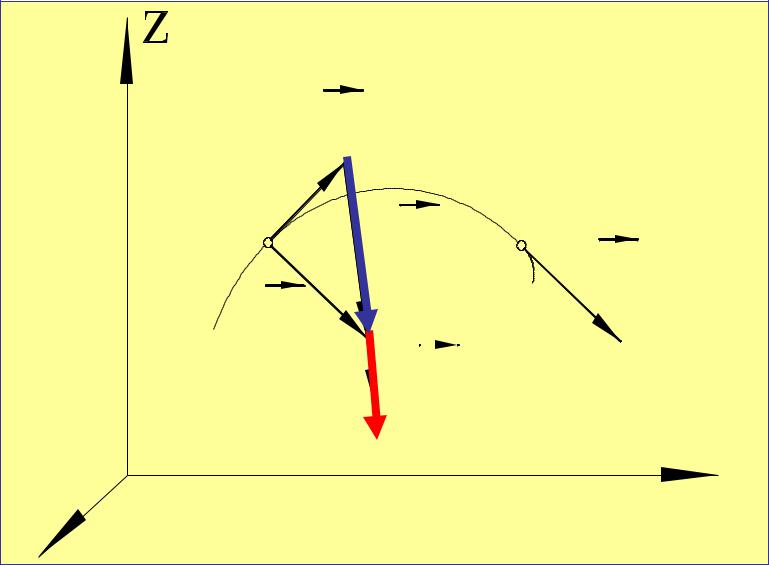
Вектор среднего ускорения |
a |
направлен по |
вектору v .
|
1 |
V1 |
2 |
|
|
|
V |
||
|
V2 |
<a> |
2 |
|
|
|
|||
|
|
|
|
|
x |
0 |
|
|
y |