7.2. Методы кластерного анализа

Непосредственными данными для применения любого метода кластери­зации является матрица различий между всеми парами объектов. Определе­ние или задание меры различия является первым и необходимым шагом кла­стерного анализа.

Из всего множества методов кластеризации наиболее распространены так называемые иерархические агломеративные методы. Название указывает на то, что классификация осуществляется путем последовательного объединения (агломерации) объектов в группы, оказывающиеся в результате иерархически организованными. Эти методы — очень простые комбинаторные процедуры, отличающиеся кри­терием объединения объектов в кластеры.

Критерий объединения многократно при­меняется ко всей матрице попарных расстоя­ний между объектами. На первых шагах объе­диняются наиболее близкие объекты, нахо­дящиеся на одном уровне сходства. Затем поочередно присоединяются остальные объ­екты, пока все они не объединятся в один боль­шой кластер. Результат работы метода представ­ляется графически в виде дендрограммы - вет­вистого древовидного графика.

Существуют различные методы иерархичес­кого кластерного анализа, в частности, в прог­рамме SPSS предлагается 7 методов. Каждый ме­тод дает свои результаты кластеризации, но три из них являются наиболее типичными. Поэто­му рассмотрим результаты применения этих ме­тодов к одним и тем же данным из примера рис.4.

Dendrogram using Single Linkage

Rescaled Distance Cluster Combine

C A S E 0 5 10 15 20 25

Label Num

3

9

2

5

7

8

10

1

4

6

Рис. 6. Дендрограмма для 10 студентов (метод одиночной связи)

Метод одиночной связи (Single Linkage) - наиболее понятный метод, кото­рый часто называют методом «ближайшего соседа» (Nearest Neighbor). Алго­ритм начинается с поиска двух наиболее близких объектов, пара которых об­разует первичный кластер. Каждый последующий объект присоединяется к тому кластеру, к одному из объектов которого он ближе.

На рис. 6 приведен результат применения метода. Сопоставляя эту дендрограмму с рис. 4, можно заметить, что объект 4 присоединяется к клас­теру (8, 10, 1) и на том же расстоянии - к объекту 6 в связи с тем, что рассто­яние от объекта 4 до объекта 6 такое же, что и до объекта 1. Из рисунка видно, что метод имеет тенденцию к образованию длинных кластеров «цепочного» вида. Таким образом, метод имеет тенденцию образовывать небольшое число крупных кластеров. К особенностям метода можно отнести и то, что результа­ты его применения часто не дают возможности определить, как много клас­теров находится в данных.

Метод полной связи (Complete Linkage) часто называют методом «дальнего соседа» (Furthest Neighbor). Правило объединения этого метода подразумева­ет, что новый объект присоединяется к тому кластеру, самый далекий элемент которого находится ближе к новому объекту, чем самые далекие элементы дру­гих кластеров. Это правило является противоположным предыдущему и бо­лее жестким. Поэтому здесь наблюдается тенденция к выделению большего числа компактных кластеров, состоящих из наиболее похожих элементов.

Dendrogram using Single Linkage

Rescaled Distance Cluster Combine

C A S E 0 5 10 15 20 25

Label Num

3

9

2

8

10

1

5

7

4

6

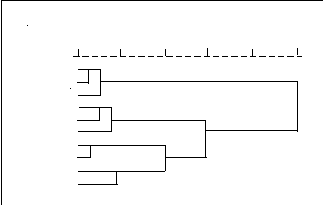
Рис.7. Дендрограмма для 10 студентов (метод полной связи)

Сравним результат применения метода полной связи (рис. 7), метода одиночной связи (рис. 6) и фактическую конфигурацию объектов (рис. 5). Различия в работе методов проявляются прежде всего в отношении объектов 4 и 6. Метод полной связи объединяет их в отдельный кластер и со­единяет с кластером (5, 7) раньше, чем с кластером (8, 10, 1) - в отличие от метода одиночной связи. Объект 4 присоединяется сначала к объекту 6, потому что этот последний к нему ближе, чем самый дальний объект кластера (8, 10, 1). На этом же основании кластер (4, 6) присоединяется к кластеру (5,7), по­тому что самый дальний объект 6 кластера (4, 6) ближе к самому дальнему объекту 7 кластера (5, 7), чем к самому дальнему объекту 8 кластера (8, 10, 1).

Метод средней связи (Average Linkage) или межгрупповой связи (Between Groups Linkage) занимает промежуточное положение относительно крайно­стей методов одиночной и полной связи. На каждом шаге вычисляется сред­нее арифметическое расстояние между каждым объектом из одного кластера и каждым объектом из другого кластера. Объект присоединяется к данному кластеру, если это среднее расстояние меньше, чем среднее расстояние до любого другого кластера. По своему принципу этот метод должен давать бо­лее точные результаты классификации, чем остальные методы. То, что объ­единение кластеров в методе средней связи происходит при расстоянии боль­шем, чем в методе одиночной связи, но меньшем, чем в методе полной связи, и объясняет промежуточное положение этого метода. Результат применения метода изображен на рис. 5. Поскольку объектов в нашем примере немно­го, результаты применения методов полной и средней связи различаются не­значительно.

В реальных исследованиях обычно имеются десятки классифицируемых объектов, и применение каждого из указанных методов дает существенно раз­ные результаты для одних и тех же данных. Опыт и литературные данные сви­детельствуют, что наиболее близкий к реальной группировке результат по­зволяет получить метод средней связи. Но это не означает бесполезность применения двух других методов. Метод одиночной связи «сжимает» про­странство, образуя минимально возможное число больших кластеров. Метод полной связи «расширяет» пространство, образуя максимально возможное число компактных кластеров. Каждый из трех методов привносит в реальное соотношение объектов свою структуру и представляет собой как бы свою точку зрения на реальность. Исследователь, в зависимости от стоящей перед ним задачи, вправе выбрать тот метод, который ему больше подходит.

Численность классов является отдельной проблемой в кластерном анали­зе. Сложность заключается в том, что не существует формальных критериев, позволяющих определить оптимальное число классов. В конечном итоге это определяется самим исследователем исходя из содержательных соображений. Однако для предварительного определения числа классов исследователь мо­жет обратиться к таблице последовательности агломерации (Agglomeration schedule). Эта таблица позволяет проследить динамику увеличения различий по шагам кластеризации и определить шаг, на котором отмечается резкое возрастание различий. Оптимальному числу классов соответствует разность между числом объектов и порядкового номера шага, на котором обнаружен перепад различий.