2.6. Неустановившееся движение электропривода при постоянном динамическом моменте

Неустановившееся механическое движение электропривода возникает во всех случаях, когда момент двигателя отличается от момента нагрузки, т.е. когда .

Рассмотрение неустановившегося движения электропривода имеет своей основной целью получение зависимостей во времени выходных механических координат электропривода – момента , скорости и положение вала двигателя . Кроме того, часто требуется определить время неустановившегося движения (переходного процесса) электродвигателя. Отметим, что законы изменения моментов двигателя и нагрузки должны быть предварительно заданы.

Рассмотрим неустановившееся движение при постоянном динамическом моменте во время пуска электродвигателя. Предполагается, что во время пуска электродвигателя и , но .

Решая уравнение механического движения электропривода, получаем следующую зависимость [2,4]:

; (2.13)

(2.14)

Уравнение (2.14) получено с учетом равенств и .

Полагая в уравнении (2.13) и , находим время изменения скорости от до

. (2.15)

Характеристики , , представлены на рисунке 2.6.

Рис. 2.6. Характеристики , , при пуске ЭД

В уравнениях (2.13), (2.14) и (2.15) момент принят равным среднему моменту при пуске двигателя, поэтому полученные выше аналитические соотношения используют только при выполнении различных приближенных расчетов в электроприводе. В частности, неустановившееся движение может быть рассмотрено при торможении и реверсе электропривода, или при переходе с одной характеристики на другую.

2.7. Неустановившееся движение электропривода при линейной зависимости моментов двигателя и исполнительного органа от скорости

Рассматриваемый вид движения является весьма распространенным.

На рисунке 2.7 представлены механические характеристики ЭД и ИО при пуске электродвигателя.

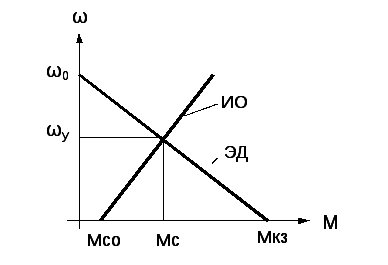
Рис. 2.7. Механические характеристики ЭД и ИО при пуске электродвигателя

Механические характеристики ЭД и ИО можно выразить аналитически следующими уравнениями:

(2.16)

(2.17)

В уравнениях (2.16) и (2.17) и – коэффициенты жесткости механических характеристик ЭД и ИО.

Подставляя выше приведенные уравнения в уравнение механического движения электропривода, получаем следующие уравнения для зависимостей , , [2,4].

(2.18)

(2.19)

(2.20)

где – электромеханическая постоянная времени в секундах, учитывающая механическую инерционность привода и влияющая на время пуска электропривода.

Полученные выражения (2.18)–(2.20) могут использоваться для анализа переходных процессов различного вида, но в каждом конкретном случае должна быть определена электромеханическая постоянная времени , а также начальные и конечные значения координат , , , . В частном случае, когда и , эти величины могут быть определены по формулам:

; (2.21)

; , (2.22)

где – это время, в течение которого электропривод запускается до скорости при . Тогда . Так как обычно момент двигателя при пуске изменяется, то на практике время пуска в секундах определяют по выражению , или по следующему выражению: .

Зависимости , приведены на рисунке 2.8.

Рис. 2.8. Зависимости , при пуске электродвигателя