
- •О. А. Заблоцкая
- •Содержание
- •Введение
- •Если функции линейные, то задача (1) называется задачей линейного программирования (лп).
- •6. Симплекс-метод
- •7. Нахождение начального базисного решения методом искусственного базиса
- •8. Двойственность в линейном программировании
- •9. Экономическая интерпретация теорем двойственности
- •Библиографический список
- •Линейное программирование Часть 1
- •Типография ОмГупСа
- •644046, Г. Омск, пр. Маркса, 35
7. Нахождение начального базисного решения методом искусственного базиса
Рассмотрим каноническую задачу ЛП:
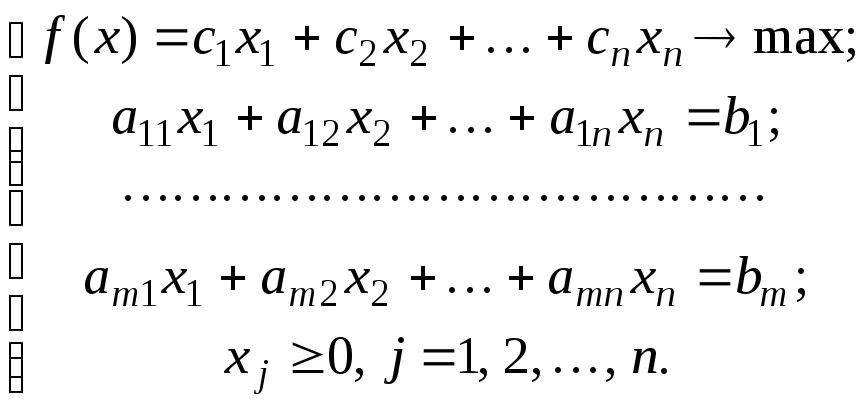 (44)
(44)
Можно
считать, что все
![]() (в противном случае соответствующее
уравнение домножим на1).
(в противном случае соответствующее
уравнение домножим на1).
Поскольку симплекс-метод может применяться для решения только специальных задач ЛП, то следует ответит на вопрос: существует ли специальная задача, эквивалентная канонической задаче (44)? И в случае положительного ответа указать способ ее построения.
Рассмотрим вспомогательную задачу ЛП:
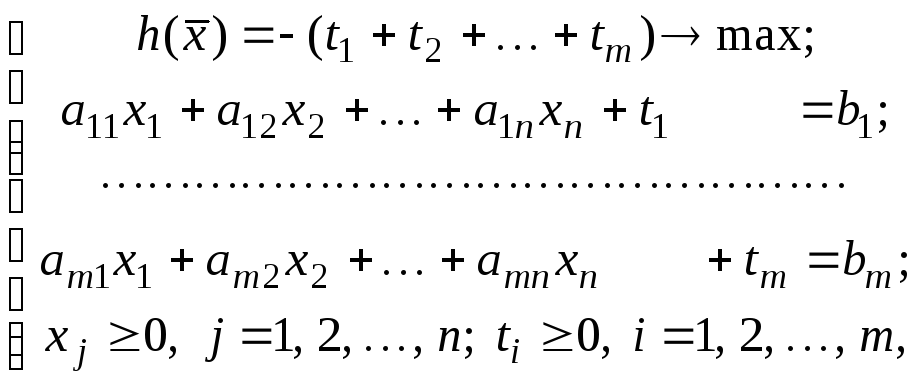 (45)
(45)
где
![]()
(n+m)-мерный
вектор. Переменные
(n+m)-мерный
вектор. Переменные
![]()
![]() называютсяискусственными
базисными переменными.
называютсяискусственными
базисными переменными.
З
а м е ч а н и е. Задача (45) легко приводится
к специальному виду. Для этого функцию
![]() надо выразить через небазисные переменные
надо выразить через небазисные переменные![]() используя линейные ограничения задачи
(45). Кроме того, отметим, что
используя линейные ограничения задачи
(45). Кроме того, отметим, что![]() при любых допустимых значениях переменных.
при любых допустимых значениях переменных.
Теорема
7 (критерий
существования допустимых решений
канонической задачи ЛП). Для канонической
задачи (44) множество D
допустимых
решений не пусто тогда и только тогда,
когда оптимальное значение целевой
функции
![]() вспомогательной задачи (45) равно нулю.
вспомогательной задачи (45) равно нулю.
Д
о к а з а т е л ь с т в о. 1) Пусть задача
(44) имеет допустимые решения и
![]()
одно из них. Тогда очевидно, что вектор
одно из них. Тогда очевидно, что вектор
![]() является допустимым решением задачи
(45). А поскольку
является допустимым решением задачи
(45). А поскольку![]() ,
то
,
то![]()
оптимальное решение задачи (45), т. е.
оптимальное решение задачи (45), т. е.
![]() .
.
2)
Пусть
![]() .
Тогда оптимальное решение задачи (45)
имеет вид:
.
Тогда оптимальное решение задачи (45)
имеет вид:![]() .
Используя связь между линейными
ограничениями задач (44) и (45), получим
допустимость вектора
.
Используя связь между линейными
ограничениями задач (44) и (45), получим
допустимость вектора![]() для канонической задачи (44). Теорема
доказана.
для канонической задачи (44). Теорема
доказана.
Теорема 8 (о преобразовании канонической задачи ЛП в эквивалентную ей специальную задачу ЛП). Если множество D допустимых решений канонической задачи (44) не пусто, то существует эквивалентная ей специальная задача ЛП, которая соответствует симплексной таблице, полученной преобразованием завершающей симплексной таблицы вспомогательной задачи (45).
Д
о к а з а т е л ь с т в о. По условию теоремы
множество допустимых решений канонической
задачи ЛП (44) не пусто. Тогда согласно
теореме 7
![]() и в оптимальном плане
и в оптимальном плане![]() вспомогательной задачи (45) все
вспомогательной задачи (45) все![]() .
.
Возможны два случая:
1)
ни одна из переменных
![]() не вошла в завершающий базис. В этом
случае удалим из полученной симплексной
таблицы отвечающие им столбцы и индексную
строку. Получим расширенную матрицу
системы линейных уравнений с базисом,
в который вошлиm
переменных из набора
не вошла в завершающий базис. В этом
случае удалим из полученной симплексной
таблицы отвечающие им столбцы и индексную
строку. Получим расширенную матрицу
системы линейных уравнений с базисом,
в который вошлиm
переменных из набора
![]() .
Выразив целевую функциюf(x)
канонической задачи ЛП (44) через небазисные
переменные, получим специальную задачу
ЛП. Она эквивалентна задаче (44), так как
получена из нее с помощью преобразований
метода Гаусса. Остается дописать новую
индексную строку, соответствующую f(x),
к рассматриваемой расширенной матрице
системы и таким образом получить
начальную симплексную таблицу для
решения канонической задачи ЛП (44);
.
Выразив целевую функциюf(x)
канонической задачи ЛП (44) через небазисные
переменные, получим специальную задачу
ЛП. Она эквивалентна задаче (44), так как
получена из нее с помощью преобразований
метода Гаусса. Остается дописать новую
индексную строку, соответствующую f(x),
к рассматриваемой расширенной матрице
системы и таким образом получить
начальную симплексную таблицу для
решения канонической задачи ЛП (44);
2)
некоторые из переменных
![]() вошли в базис завершающей симплексной
таблицы вспомогательной задачи (45). В
этом случае их можно исключить из базиса,
заменяя переменными из множества
вошли в базис завершающей симплексной
таблицы вспомогательной задачи (45). В
этом случае их можно исключить из базиса,
заменяя переменными из множества![]() с помощью преобразований Гаусса. В
результате вновь попадаем в условия
уже рассмотренного ранее первого случая.
Теорема доказана.
с помощью преобразований Гаусса. В
результате вновь попадаем в условия
уже рассмотренного ранее первого случая.
Теорема доказана.
Метод построения специальной задачи ЛП, эквивалентной канонической задаче ЛП, с помощью вспомогательной задачи называется методом искусственного базиса.
Пример 9. Решить каноническую задачу ЛП:
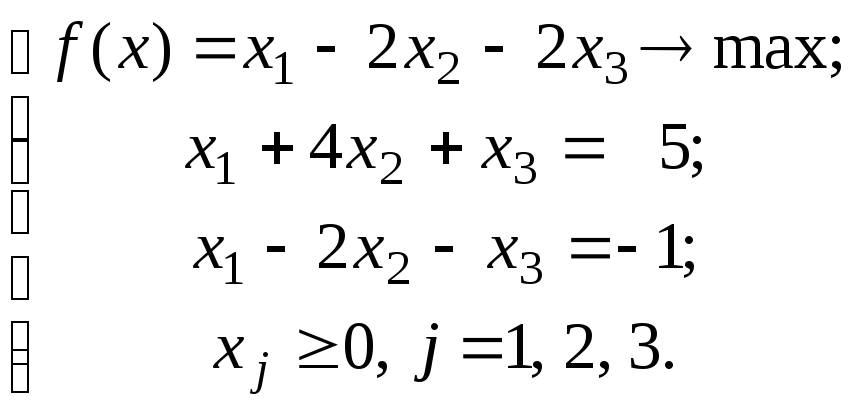 (46)
(46)
Задача (46) не является специальной, так как система ее ограничений не является системой с базисом и среди правых частей есть отрицательное число, поэтому применим метод искусственного базиса. Составим вспомогательную задачу и приведем ее к специальному виду, выражая целевую функцию через небазисные переменные:
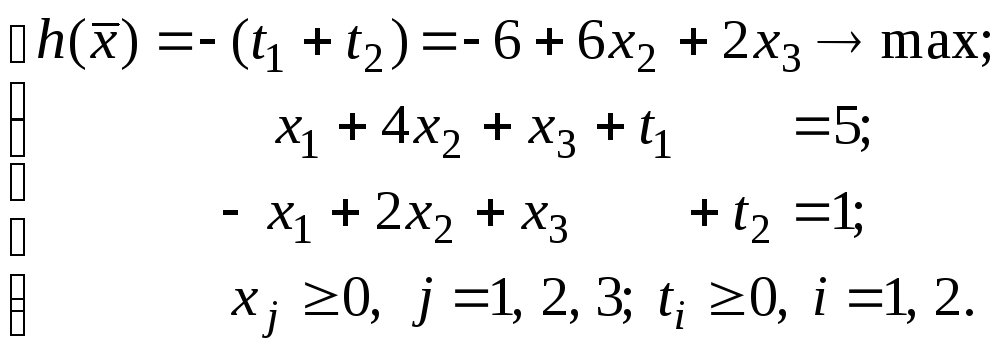 (47)
(47)
Специальную задачу ЛП (47) решаем симплекс-методом.
Т а б л и ц а 7
-
B
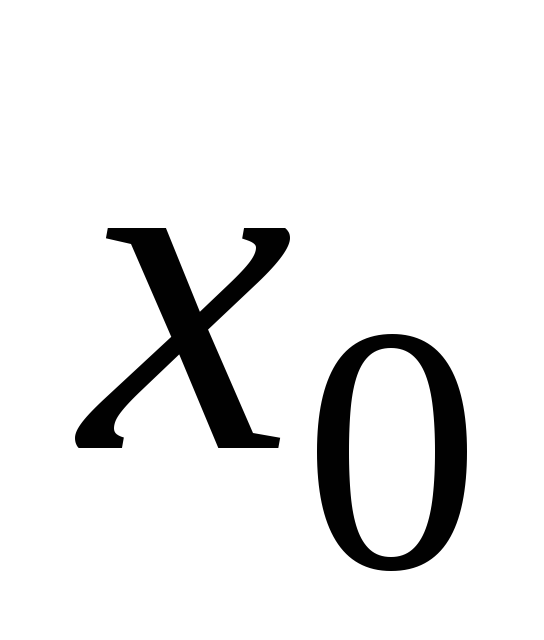
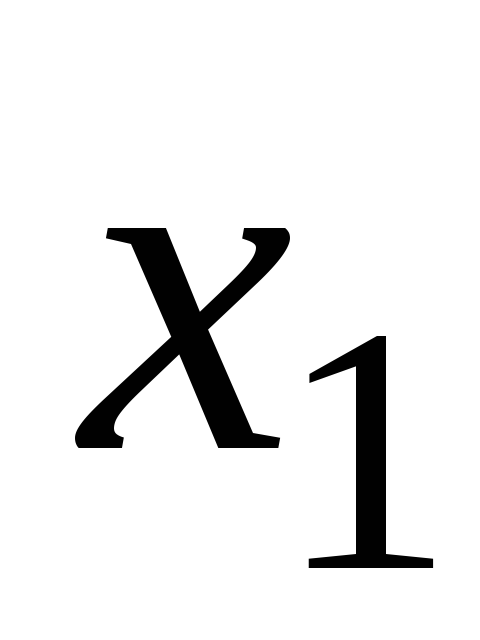
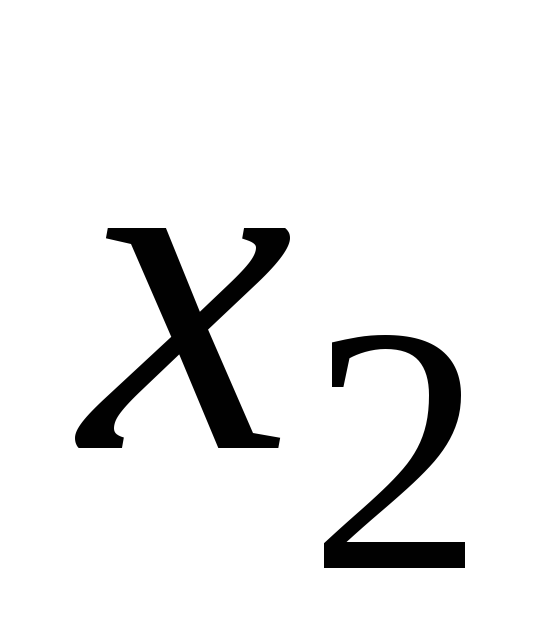
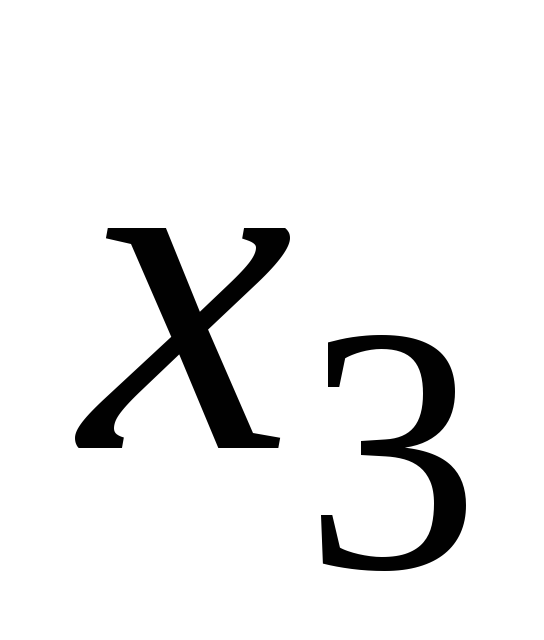
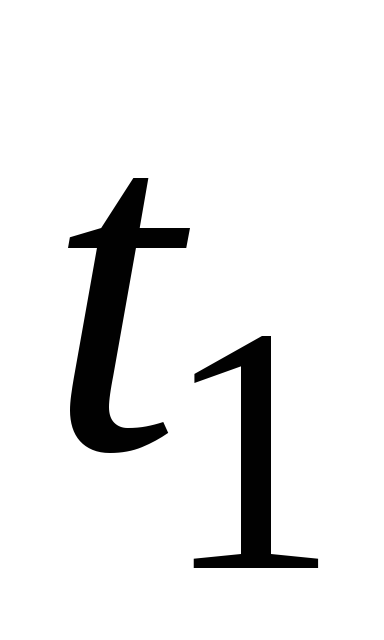
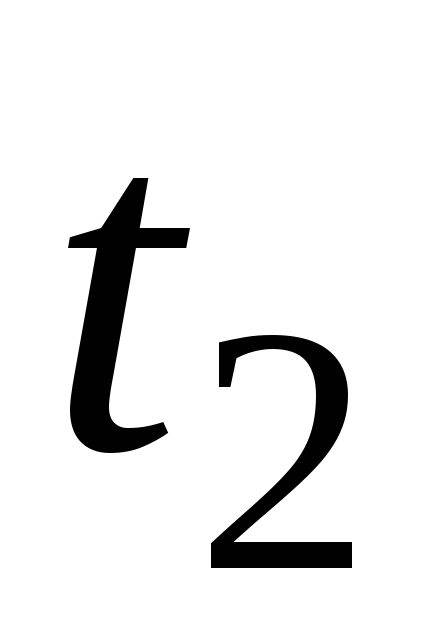
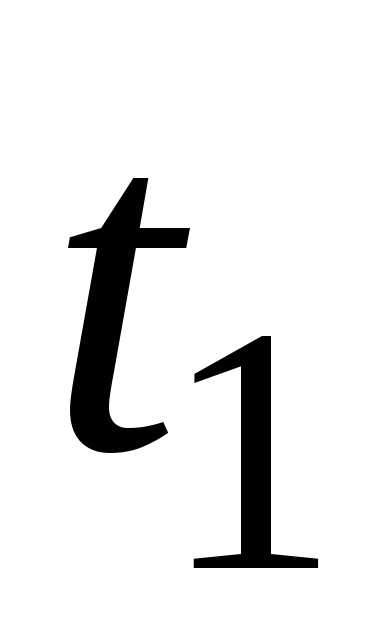
5
1
4
1
1
0
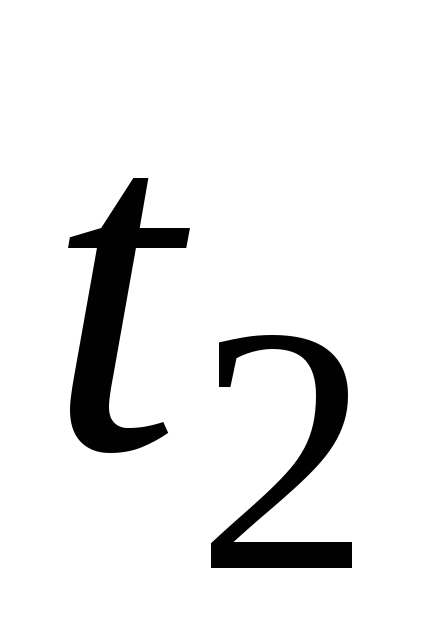
1
-1
2
1
0
1
h
-6
0
-6
-2
0
0
Т а б л и ц а 8
-
B
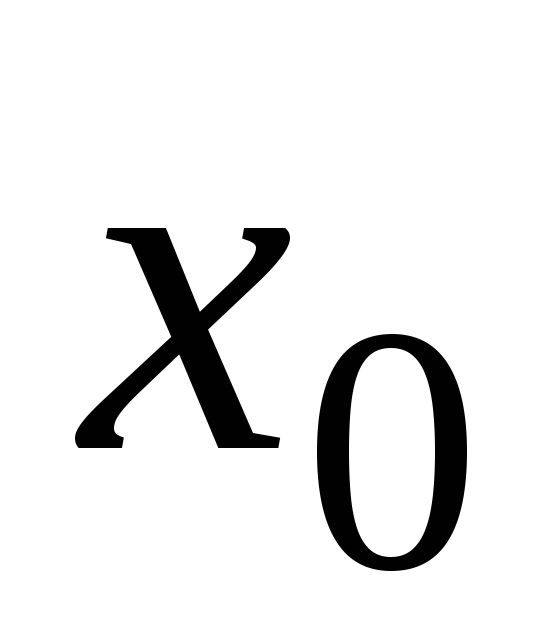
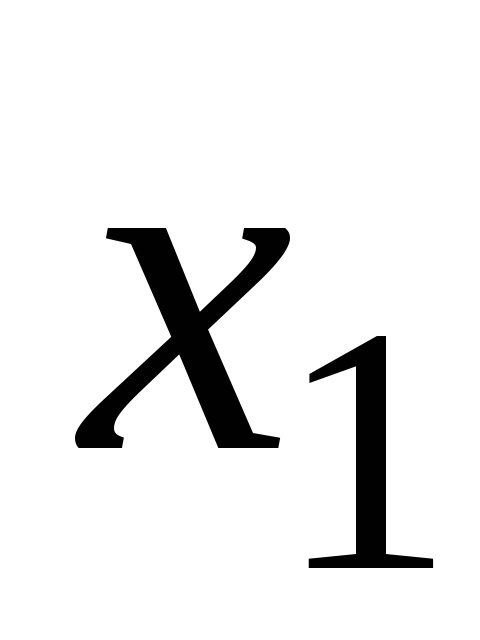
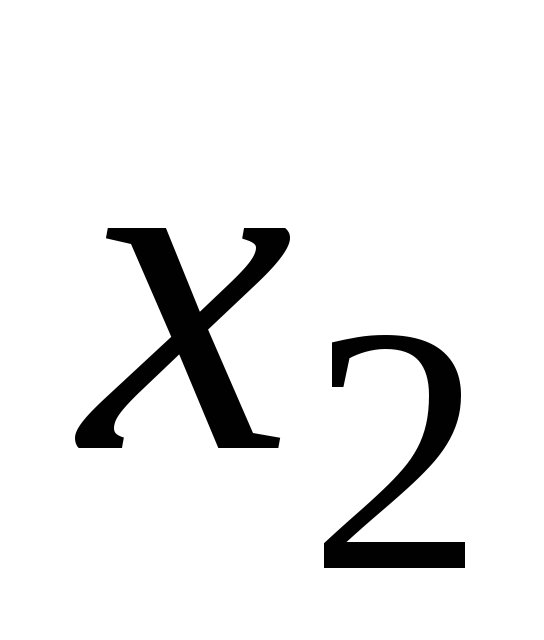
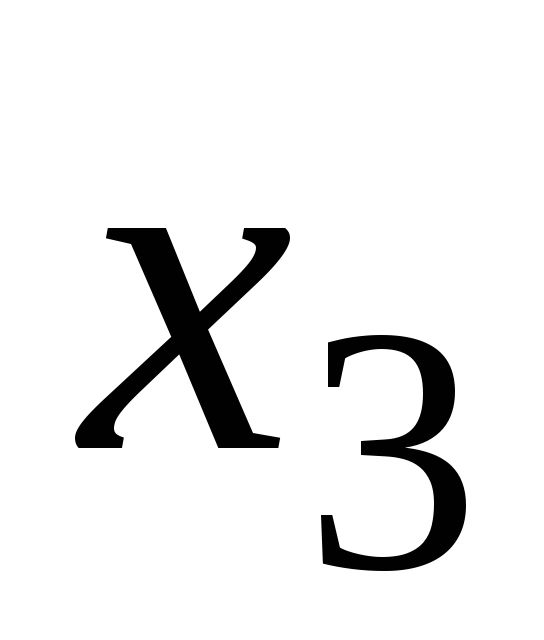
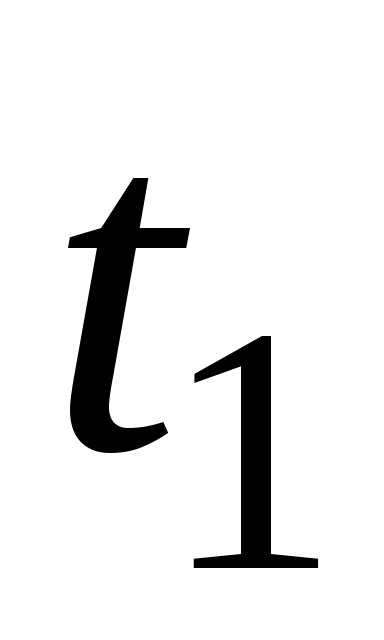
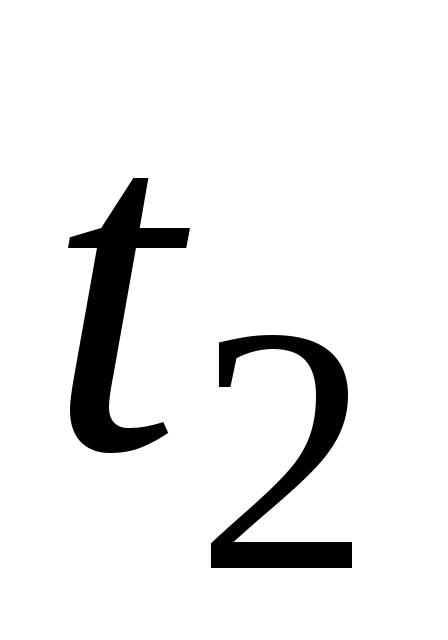
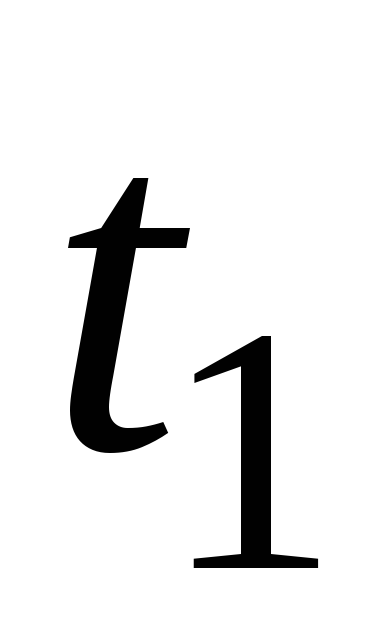
4
2
2
0
1
-1
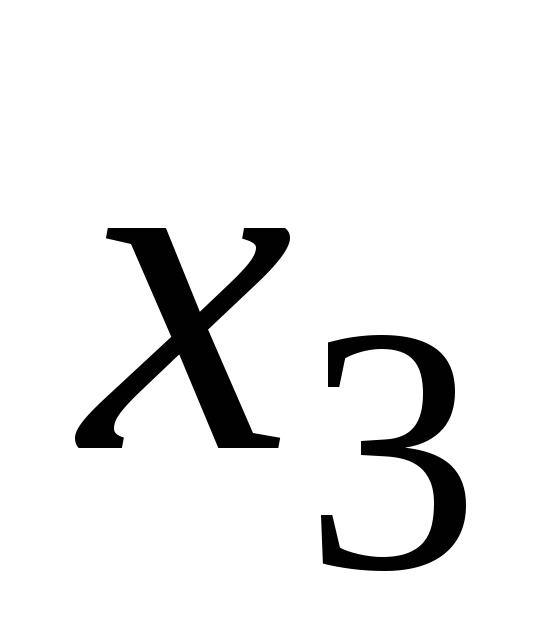
1
-1
2
1
0
1
h
-4
-2
-2
0
0
2
Т а б л и ц а 9
-
B
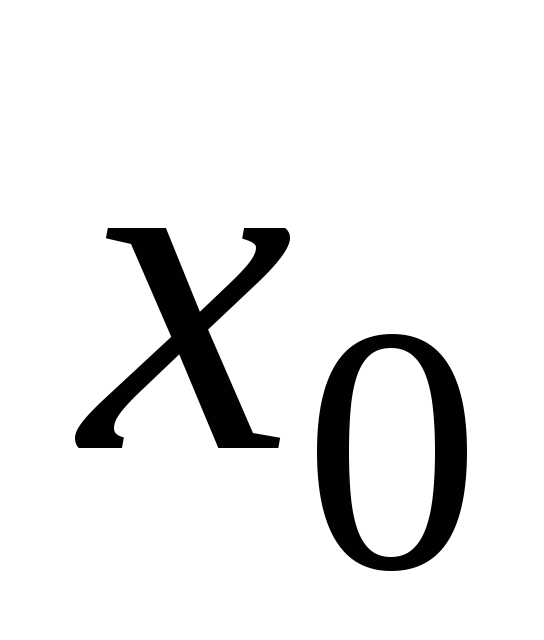
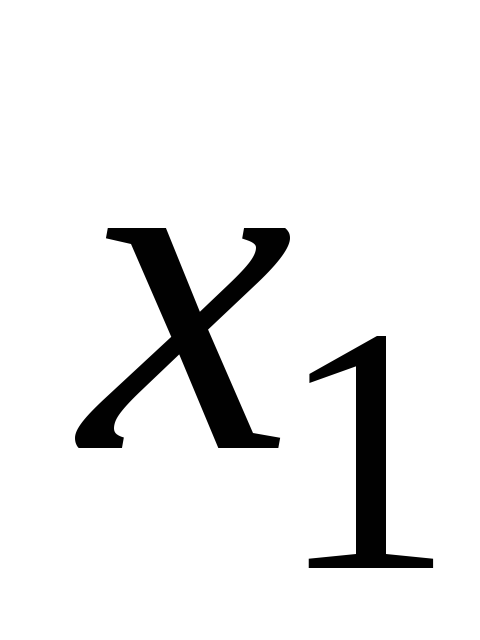
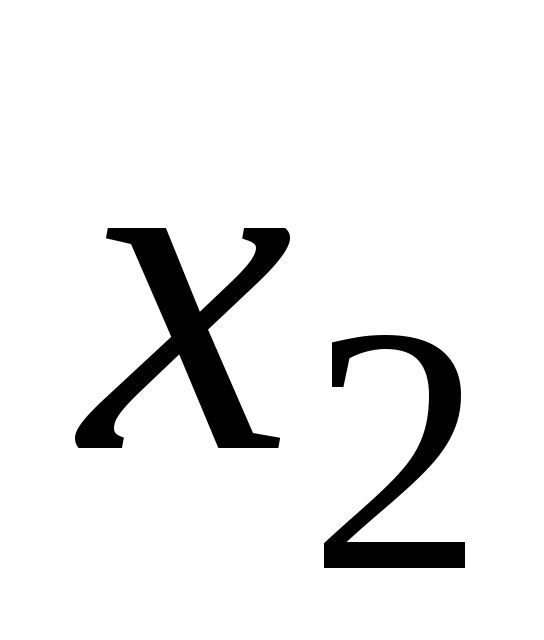
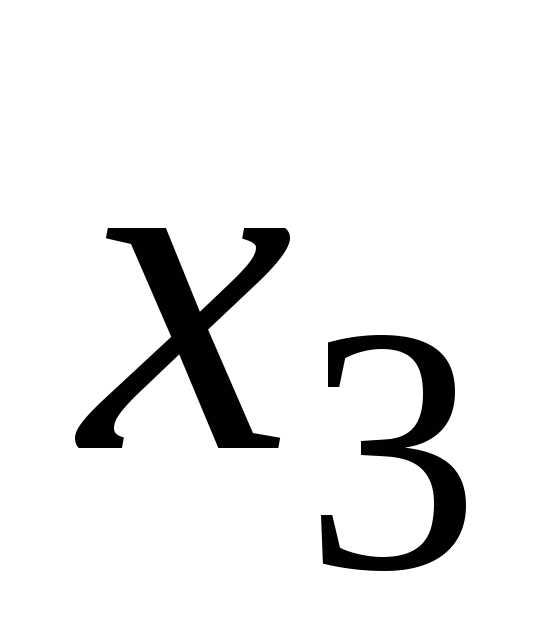
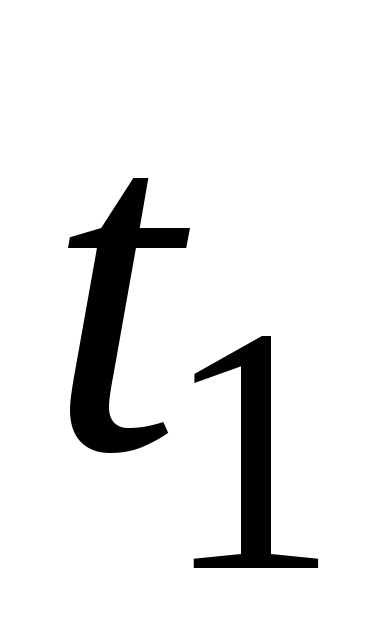
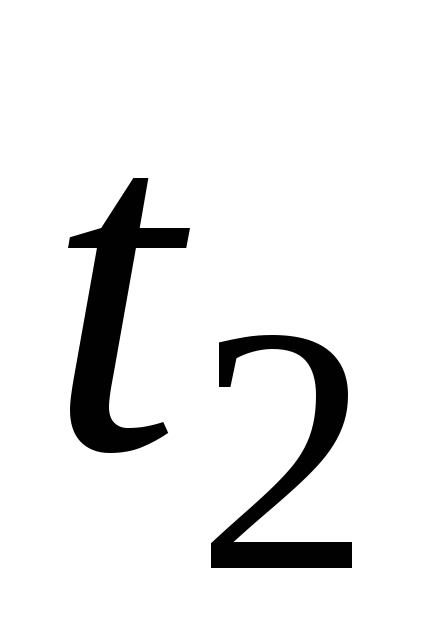

2
1
1
0
0,5
-0,5
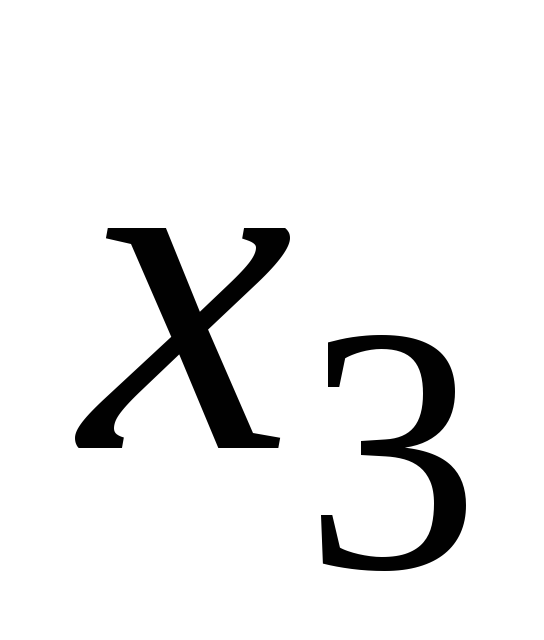
3
0
3
1
0,5
0,5
h
0
0
0
0
1
1
Так
как
![]() ,
то множествоD
допустимых решений канонической задачи
ЛП (45) не пусто. Следовательно, по теореме
8 существует специальная задача,
эквивалентная задаче (45). Эта задача
имеет следующий вид:
,
то множествоD
допустимых решений канонической задачи
ЛП (45) не пусто. Следовательно, по теореме
8 существует специальная задача,
эквивалентная задаче (45). Эта задача
имеет следующий вид:
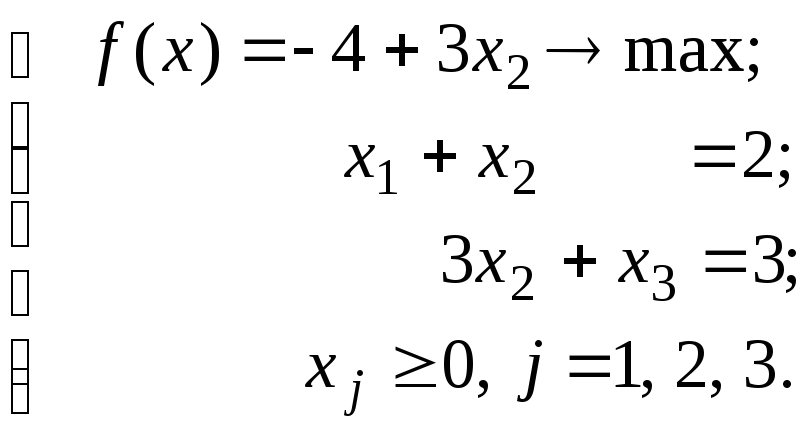 (48)
(48)
Линейные
ограничения этой системы получены из
завершающей симплексной табл. 9
вспомогательной задачи, а целевая
функция исходной задачи (46) приняла вид
![]() после подстановки в нее выражений
после подстановки в нее выражений![]() ;
;![]() .
.
Решаем специальную задачу ЛП (48) симплекс-методом (табл. 10, 11).
Т а б л и ц а 10
|
B |
|
|
|
|
|
|
2 |
1 |
1 |
0 |
|
|
3 |
0 |
3 |
1 |
|
f |
-4 |
0 |
-3 |
0 |
Т а б л и ц а 11
|
B |
|
|
|
|
|
|
1 |
1 |
0 |
-13 |
|
|
1 |
0 |
1 |
13 |
|
f |
-1 |
0 |
0 |
1 |
Итак,
получили оптимальное базисное решение
исходной канонической задачи (46):
![]() ;
;![]() .
.
