
Образец выполнения контрольной работы № 1
“МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ”
Вычислить определители
а)
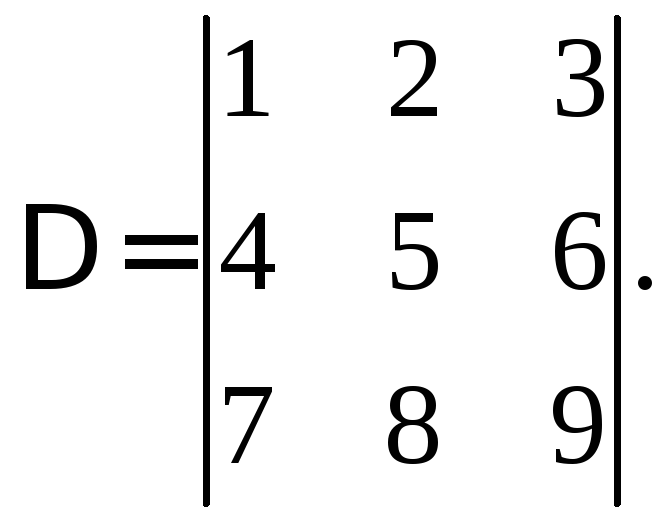
Решение. Этот определитель вычислим по правилу диагоналей. Приписываем справа к определителю первый и второй столбцы. Перемножаем элементы, стоящие на главной диагонали и складываем это произведение с аналогичными произведениями элементов, стоящих на диагоналях, параллельных главной. Затем к произведению элементов, стоящих на побочной диагонали, прибавляем аналогичные произведения элементов, стоящих на диагоналях, параллельных побочной. Затем от первой суммы вычитаем вторую. Это и будет искомый определитель.
7 8 9 7 8 |
|
Ответ:
![]()
б)

Решение. Решение найдем разложением по первому столбцу, но сначала с помощью свойств определителя сделаем нули в этом столбце везде кроме элемента, равного минус единице.
Для этого элементы второй строки умножим на два и прибавим к соответствующим элементампервойстроки; элементывторой строки прибавим к соответствующим элементамтретьейстроки; элементывторойстроки умножим на два и прибавим к соответствующим элементамчетвертойстроки. Эти действия записываем так:
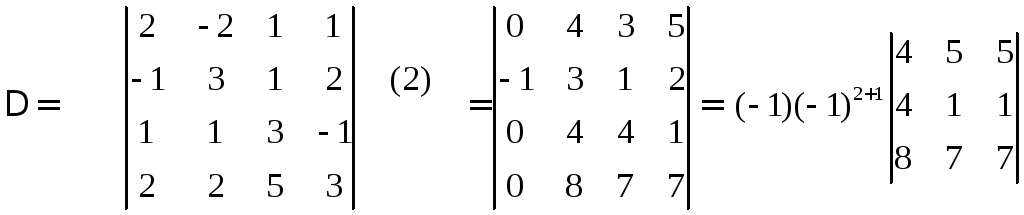
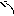

 .
.
Разложив определитель 4-го порядка по
1-му столбцу, свели его вычисление к
нахождению одного определителя 3-го
порядка, который можно вычислить по
правилу диагоналей, разобранному выше.
Можно дальше применить свойства
определителя и свести этот определитель
к одному определителю 2-го порядка.
Продолжаем делать нули теперь уже во
второй строке, умножая элементы третьего
столбца на
![]() и прибавляя к первому и второму столбцам:
и прибавляя к первому и второму столбцам:
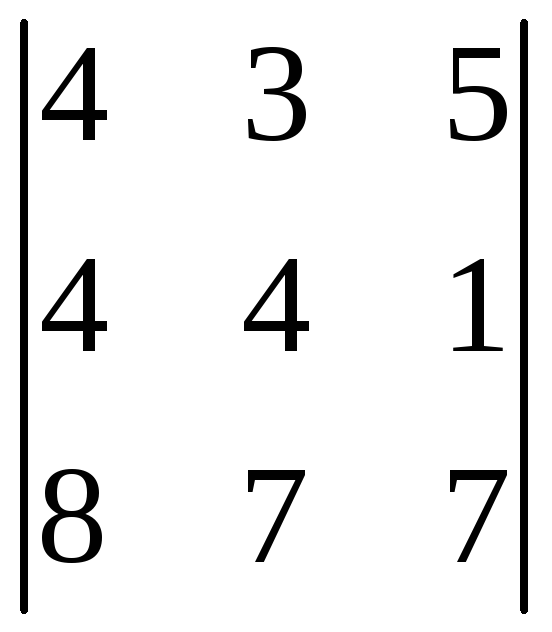

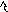
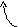
 =
=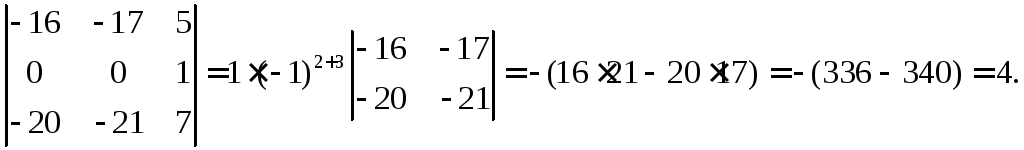
(-4)
(-4)
Ответ:![]()
Умножить матрицы:
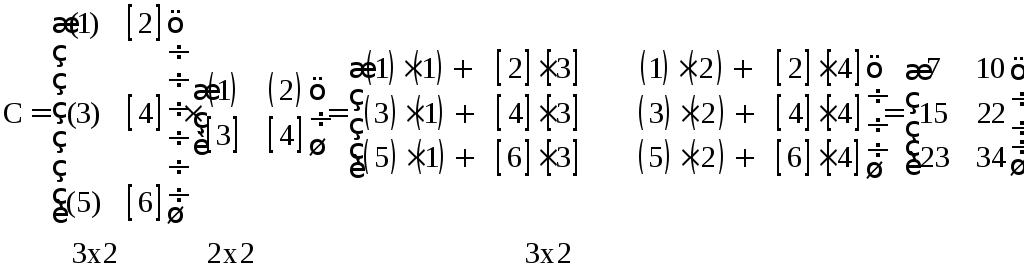


 .
.
Решение. Произведение матриц получили, умножая элементы строк первой матрицы на соответствующие элементы столбцов второй матрицы и складывая их.
Ответ: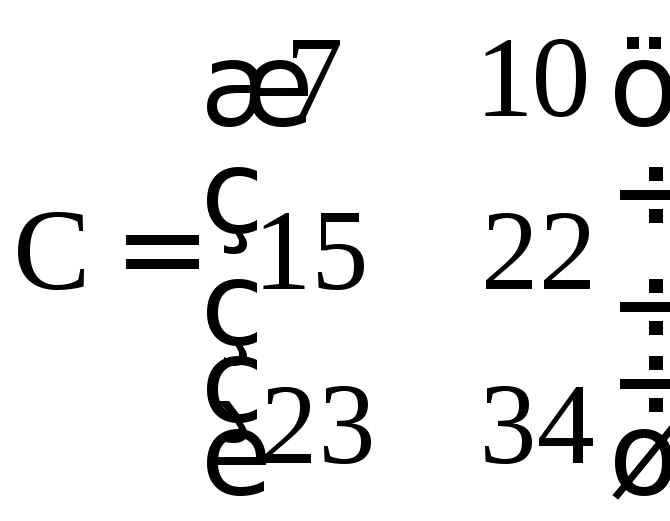 .
.
3) Найти обратные матрицы:
а)
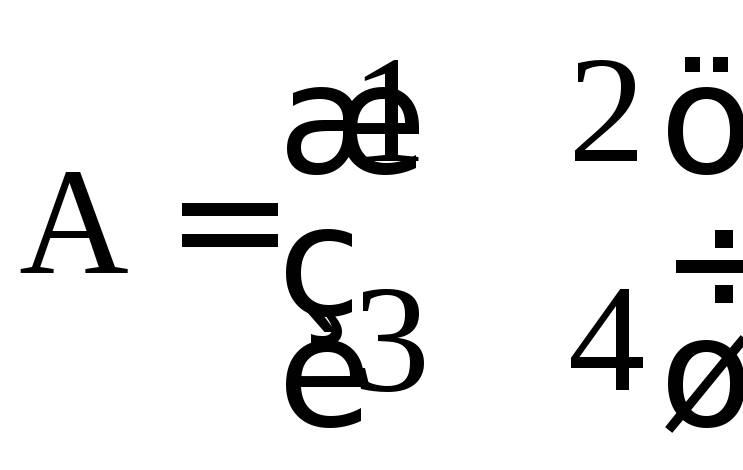
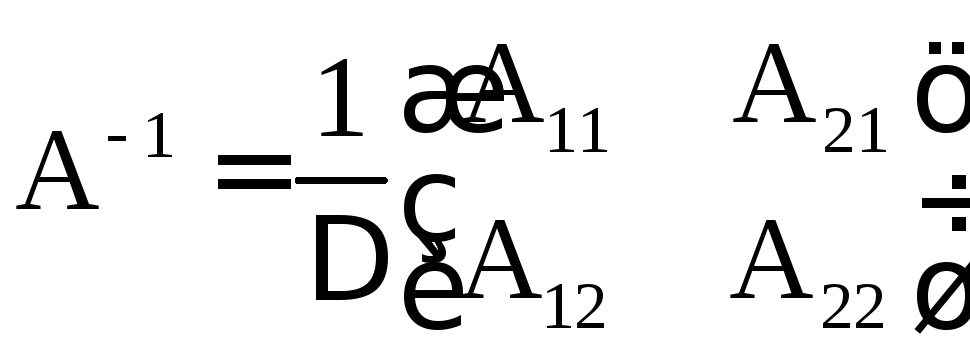 .
.
Решение. Сначала находим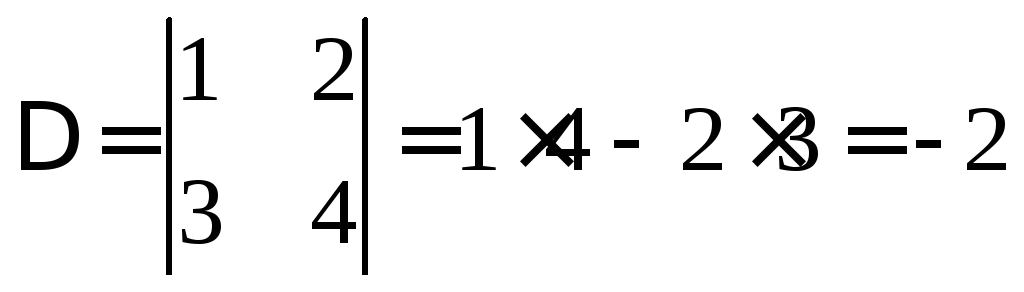 ;
;![]() ,
значит, существует матрица
,
значит, существует матрица![]() .
Находим алгебраические дополнения:
.
Находим алгебраические дополнения:







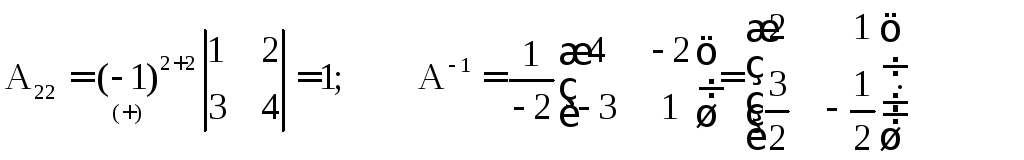


Ответ: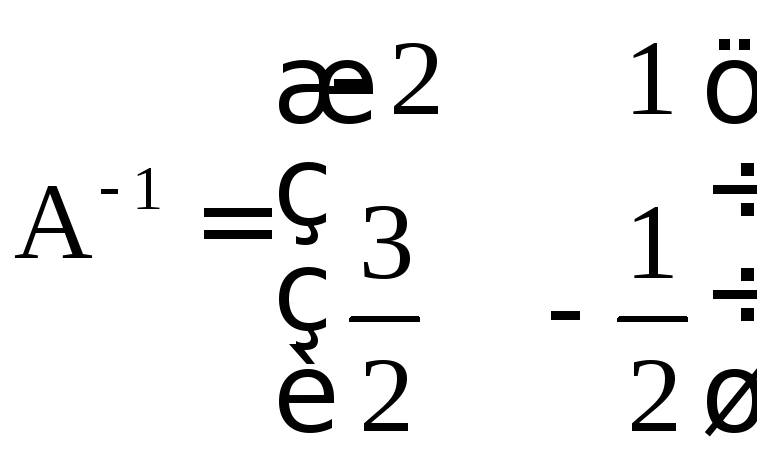 .
.
4) Найти двумя способами ранг матрицы:
 .
.
Решение.
1 способ. Метод окаймляющих миноров.Находим любой минор второго по
рядка, отличный от нуля, например
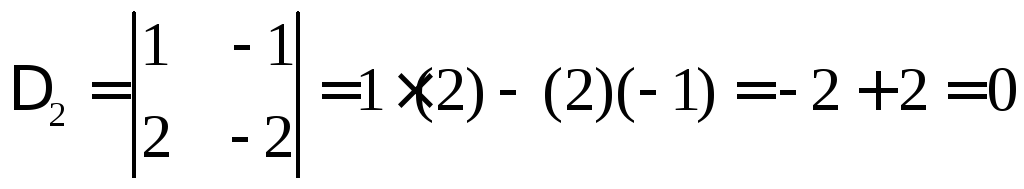 ,
по-
,
по-
этому выписываем другой определитель
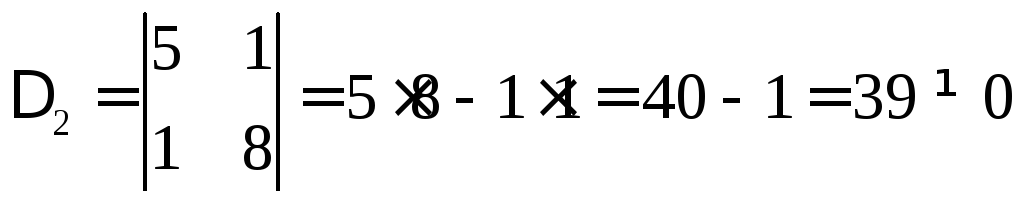 .
Нашелся определитель второго порядка,
отличный от нуля, значит ранг
.
Нашелся определитель второго порядка,
отличный от нуля, значит ранг![]() .
Теперь найдем определитель третьего
порядка, окаймляющий найденный
.
Теперь найдем определитель третьего
порядка, окаймляющий найденный![]() .
.
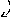


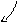
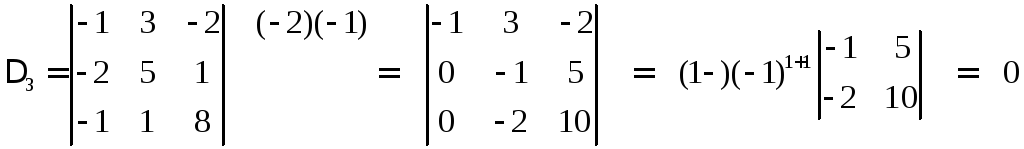
Берем
другой определитель, окаймляющий
![]()
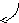

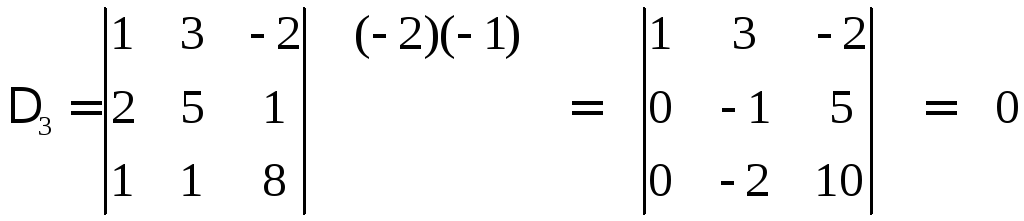 ,
как и предыдущий.
,
как и предыдущий.
Больше окаймляющих миноров третьего
порядка для
![]() нет, поэтому ранг А, равный наивысшему
порядку минора, отличного от нуля, равен
двум.
нет, поэтому ранг А, равный наивысшему
порядку минора, отличного от нуля, равен
двум.
2 Способ. Метод элементарных преобразований.






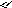
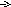
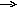 .
.
Получили
2-е нулевые строки. Поэтому ранг А равен
2 (очевидно минор второго порядка
 ).
).
Ответ:![]() .
.
Контрольная работа № 2
“СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ”
ЗАДАНИЕ 1. Решить системы матричным способом и по формулам Крамера:
|
1. |
а)
|
б)
|
|
2. |
а)
|
б)
|
|
3. |
а)
|
б)
|
|
4. |
a)
|
б)
|
|
5. |
а)
|
б)
|
|
6. |
а)
|
б)
|
|
7. |
а)
|
б)
|
|
8. |
а)
|
б)
|
|
9. |
а)
|
б)
|
|
10. |
а)
|
б)
|
|
11. |
а)
|
б)
|
|
12. |
а)
|
б)
|
|
13. |
а)
|
б)
|
|
14. |
а)
|
б)
|
|
15. |
а)
|
б)
|
|
16. |
а)
|
б)
|
|
17. |
а)
|
б)
|
|
18. |
а)
|
б)
|
|
19. |
а)
|
б)
|
|
20. |
a)
|
б)
|
|
21. |
а)
|
б)
|
|
22. |
а)
|
б)
|
|
23. |
а)
|
б)
|
|
24. |
а)
|
б)
|
|
25. |
а)
|
б)
|
|
26. |
а)
|
б)
|
|
27. |
а)
|
б)
|
|
28. |
а)
|
б)
|
|
29. |
а)
|
б)
|
|
30. |
а)
|
б)
|
Задание 2. Решить системы методом Гаусса:
|
1. |
а)
|
б)
|
|
в)
|
г)
| |
|
2. |
а)
|
б)
|
|
в)
|
г)
| |
|
3. |
а)
|
б)
|
|
в)
|
г)
| |
|
4. |
а)
|
б)
|
|
в)
|
г)
| |
|
5. |
а)
|
б)
|
|
в)
|
г)
| |
|
6. |
а)
|
б)
|
|
в)
|
г)
| |
|
7. |
а)
|
б)
|
|
в)
|
г)
| |
|
8. 8. |
а)
|
б)
|
|
в)
|
г)
| |
|
9. |
а)
|
б)
|
|
в)
|
г)
| |
|
10. |
а)
|
б)
|
|
в)
|
г)
| |
|
11. |
а)
|
б)
|
|
в)
|
г)
| |
|
12.
|
а)
|
б)
|
|
в)
|
г)
| |
|
13. |
а)
|
б)
|
|
в)
|
г)
| |
|
14. |
а)
|
б)
|
|
в)
|
г)
| |
|
15. |
а)
|
б)
|
|
в)
|
г)
| |
|
16. |
а)
|
б)
|
|
в)
|
г)
| |
|
17. |
а)
|
б)
|
|
в)
|
г)
| |
|
18. |
а)
|
б)
|
|
в)
|
г)
| |
|
19. |
а)
|
б)
|
|
в)
|
г)
| |
|
20. |
а)
|
б)
|
|
в)
|
г)
| |
|
21. |
а)
|
б)
|
|
в)
|
г)
| |
|
22. |
а)
|
б)
|
|
в)
|
г)
| |
|
23. |
а)
|
б)
|
|
в)
|
г)
| |
|
24.
|
а)
|
б)
|
|
в)
|
г)
| |
|
25. |
а)
|
б)
|
|
в)
|
г)
| |
|
26. |
а)
|
б)
|
|
в)
|
г)
| |
|
27. |
а)
|
б)
|
|
в)
|
г)
| |
|
28.
|
а)
|
б)
|
|
в)
|
г)
| |
|
29. |
а)
|
б)
|
|
в)
|
г)
| |
|
30. |
а)
|
б)
|
|
в)
|
г)
|
Задание 3. Решить системы однородных уравнений:
|
1. |
а)
|
б)
|
|
2. |
а)
|
б)
|
|
3. |
а)
|
б)
|
|
4. |
а)
|
б)
|
|
5. |
а)
|
б)
|
|
6. |
а)
|
б)
|
|
7. |
а)
|
б)
|
|
8. |
а)
|
б)
|
|
9. |
а)
|
б)
|
|
10. |
а)
|
б)
|
|
11. |
а)
|
б)
|
|
12. |
а)
|
б)
|
|
13. |
а)
|
б)
|
|
14. |
а)
|
б)
|
|
15. |
а)
|
б)
|
|
16. |
а)
|
б)
|
|
17. |
а)
|
б)
|
|
18. |
а)
|
б)
|
|
19. |
а)
|
б)
|
|
20. |
а)
|
б)
|
|
21. |
а)
|
б)
|
|
22. |
а)
|
б)
|
|
23. |
а)
|
б)
|
|
24. |
а)
|
б)
|
|
25. |
а)
|
б)
|
|
26. |
а)
|
б)
|
|
27. |
а)
|
б)
|
|
28. |
а)
|
б)
|
|
29. |
а)
|
б)
|
|
30. |
а)
|
б)
|






 2 3 1
2
2 3 1
2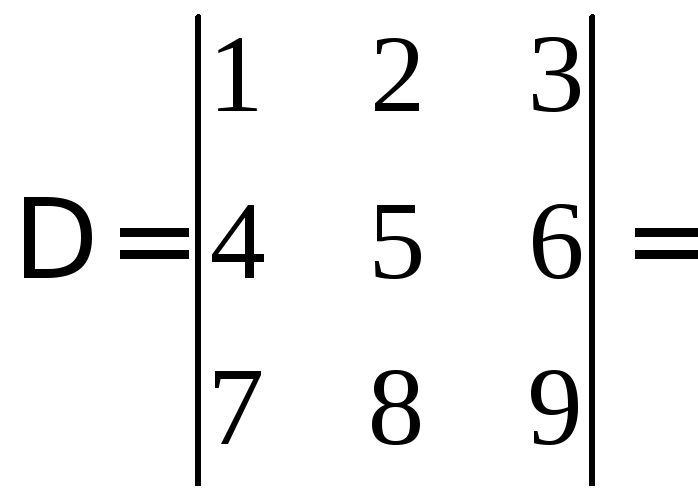
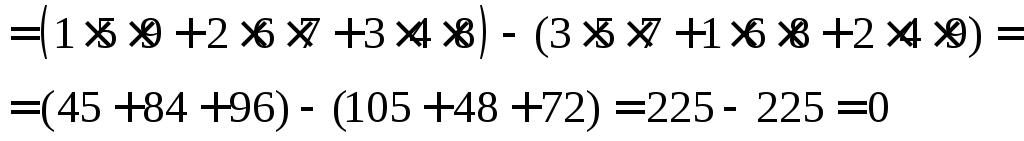
 ;
;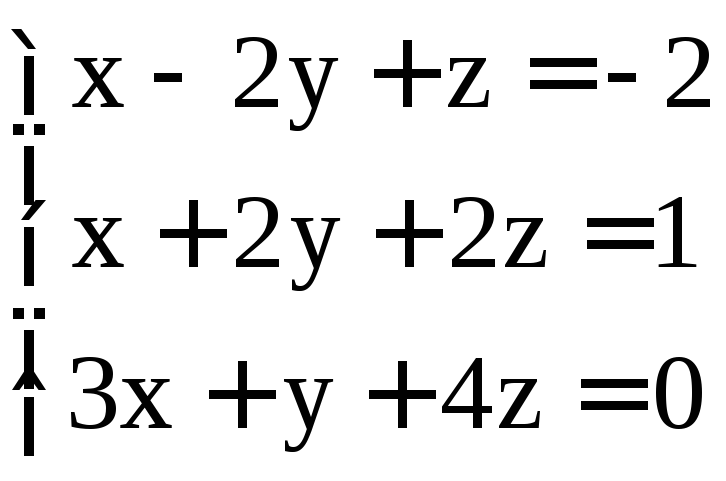 .
.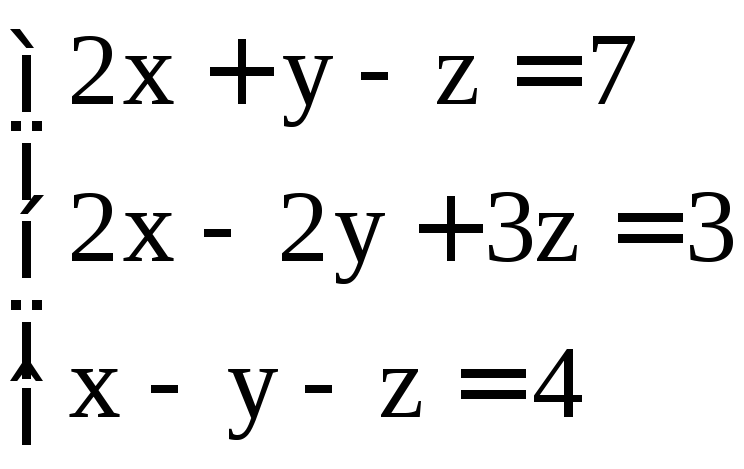 ;
;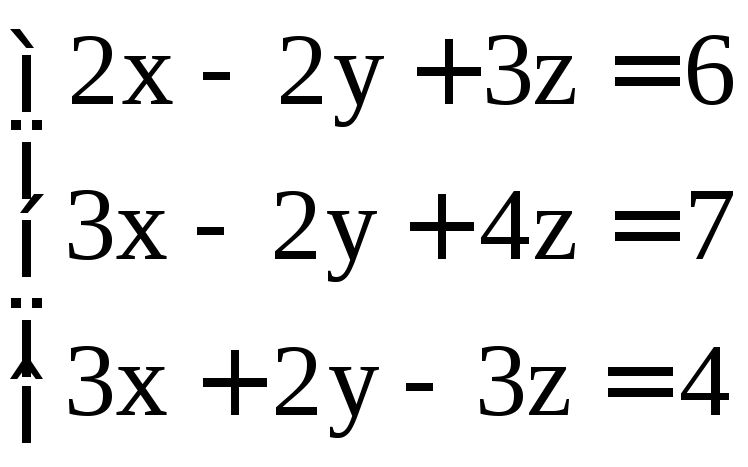 .
.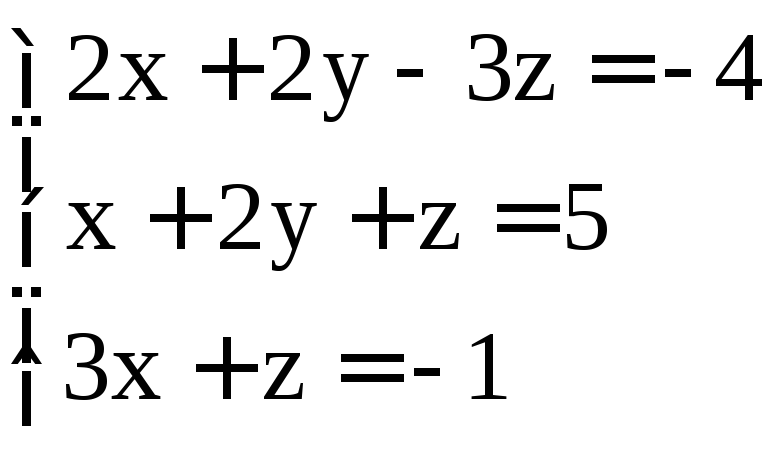 ;
;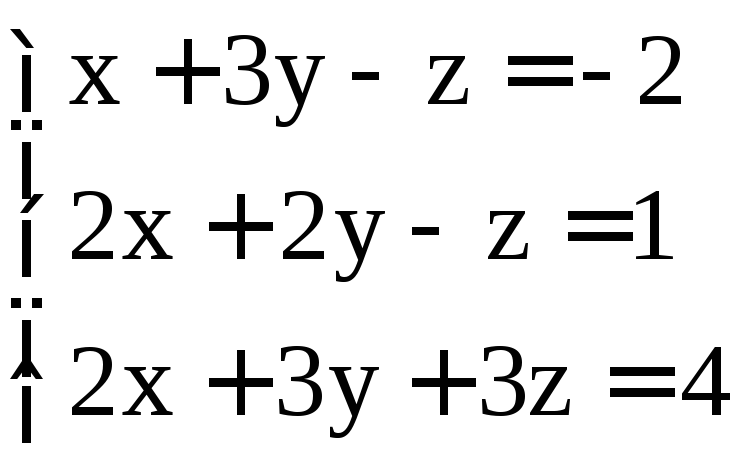 .
. ;
;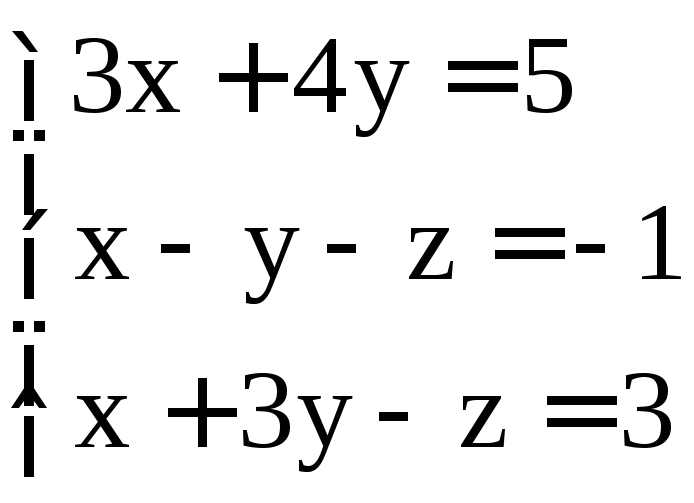 .
.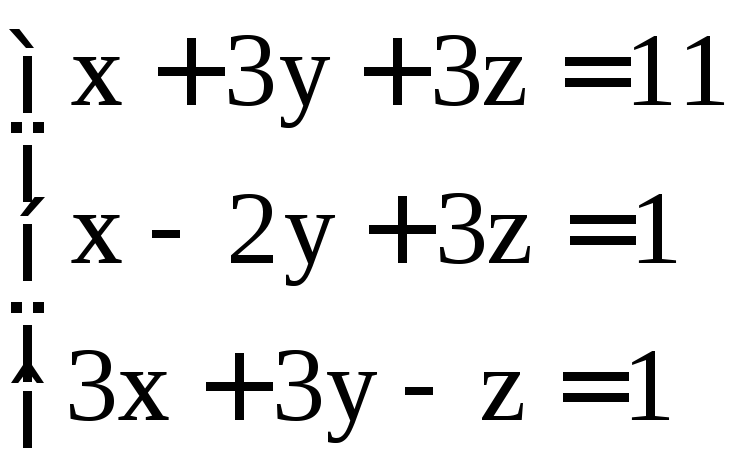 ;
;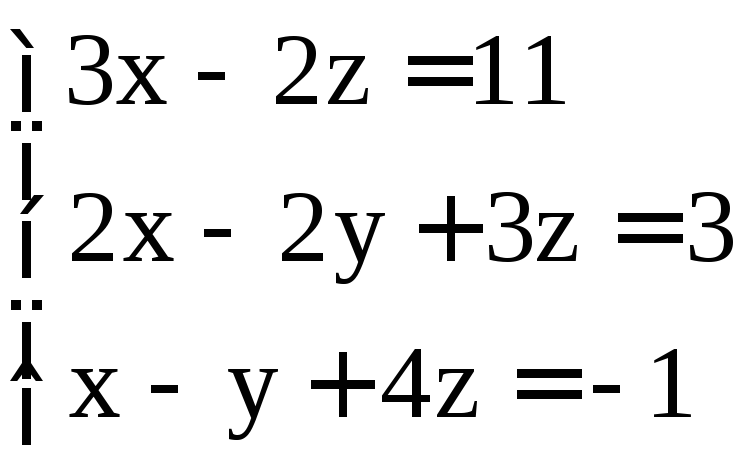 .
. ;
;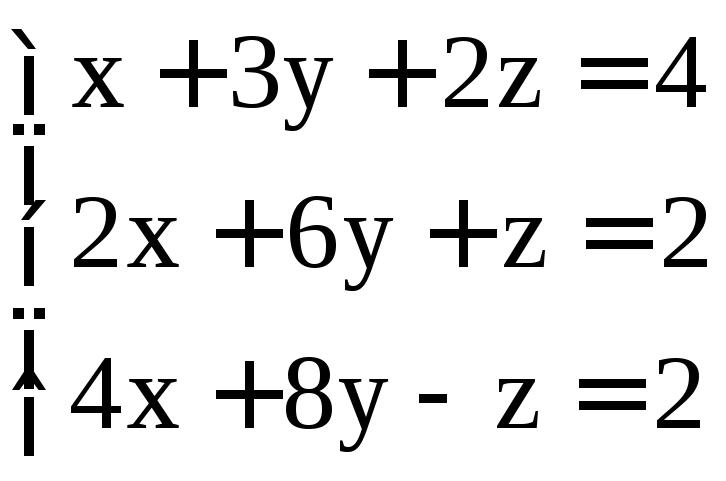 .
.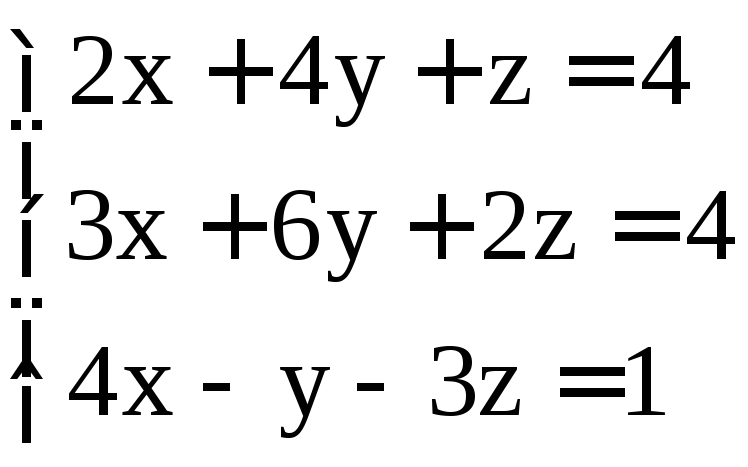 ;
;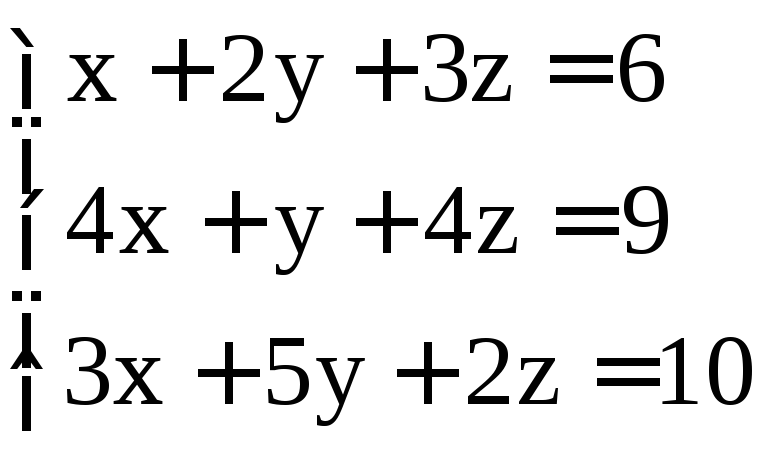 .
. ;
;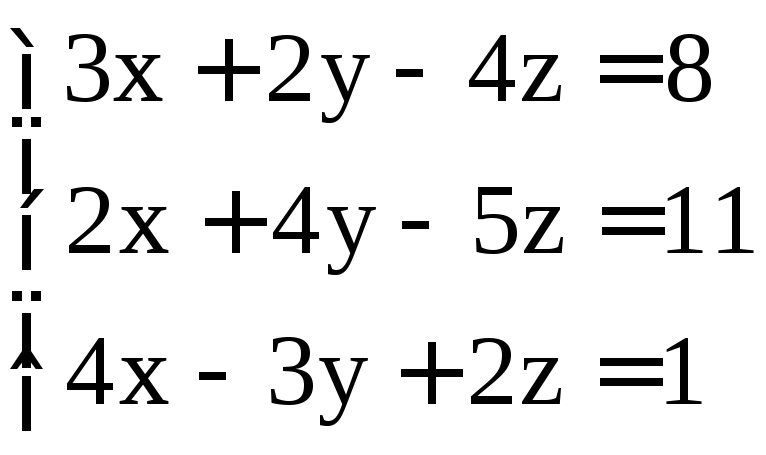 .
.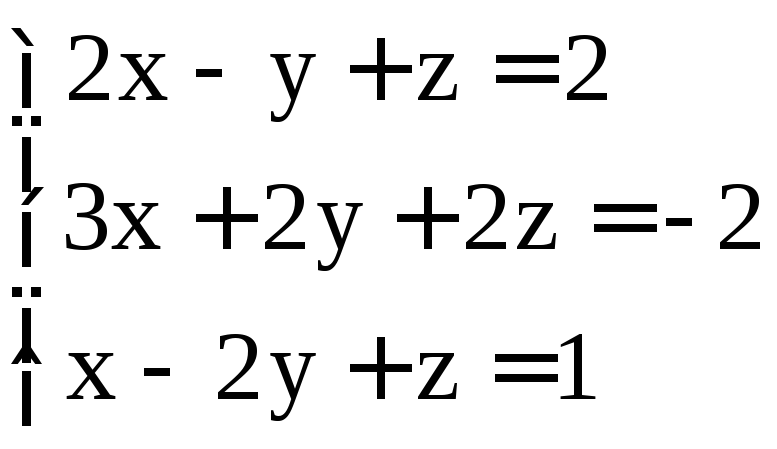 ;
;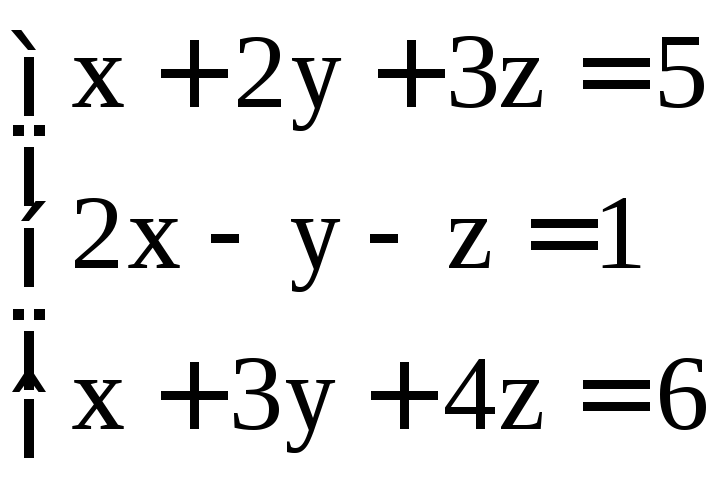 .
.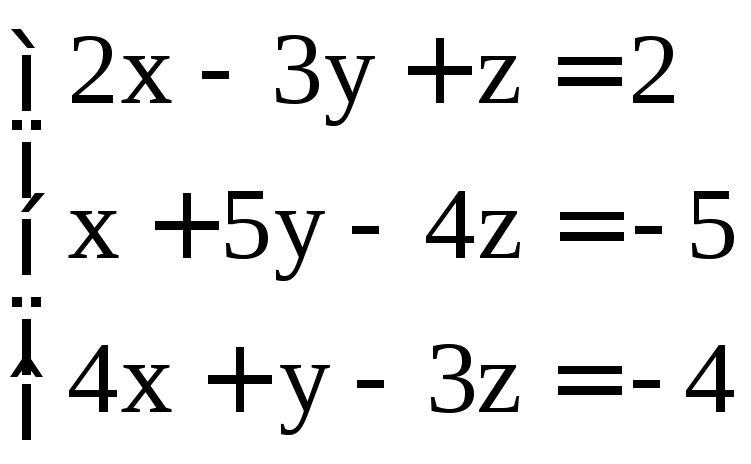 ;
;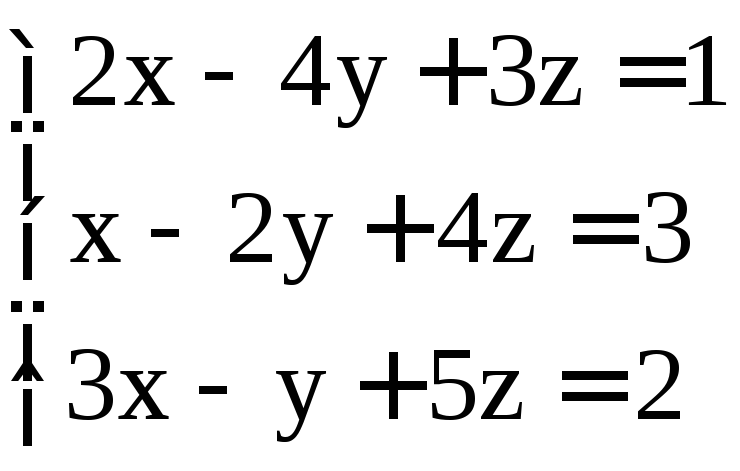 .
.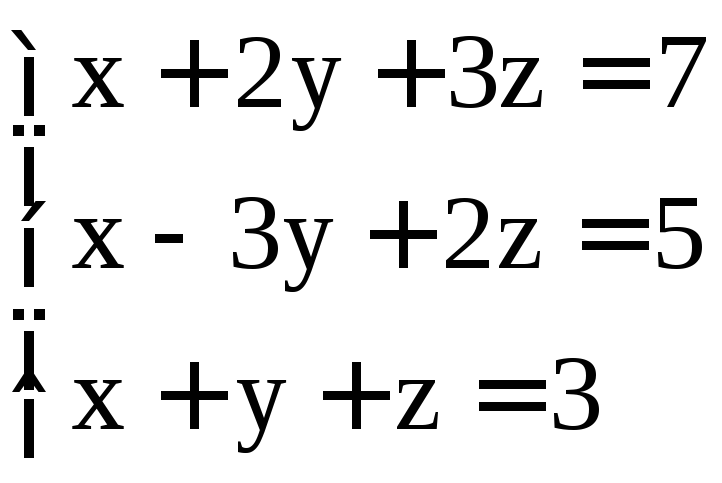 ;
;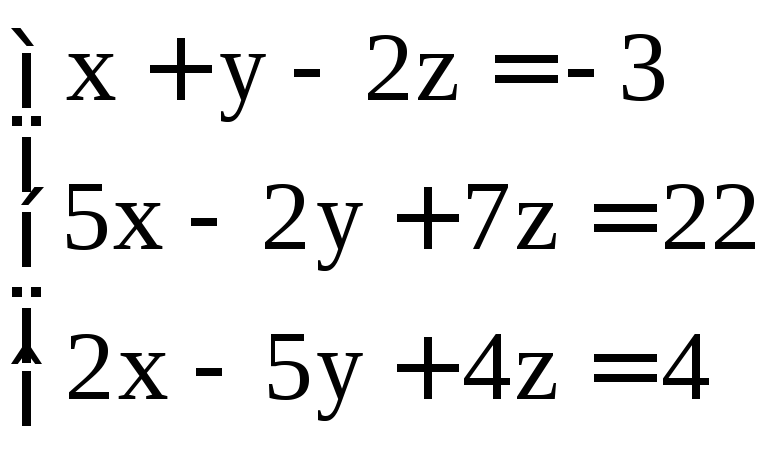 .
.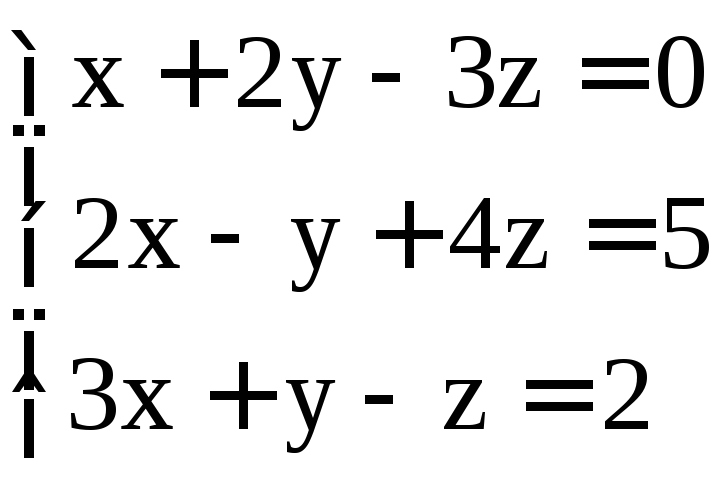 ;
;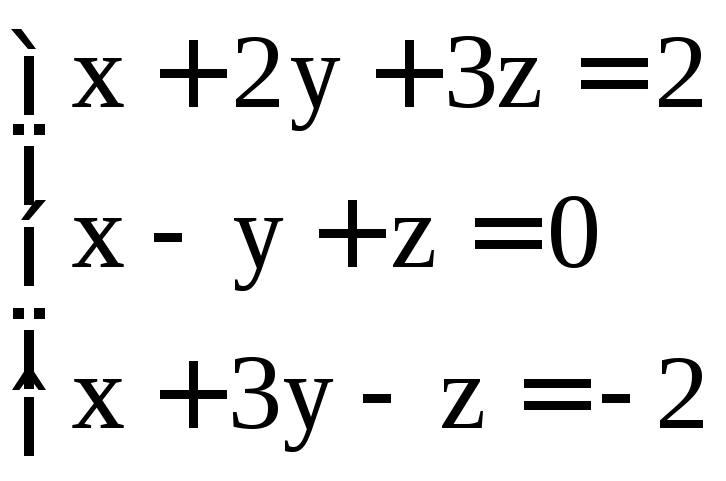 .
.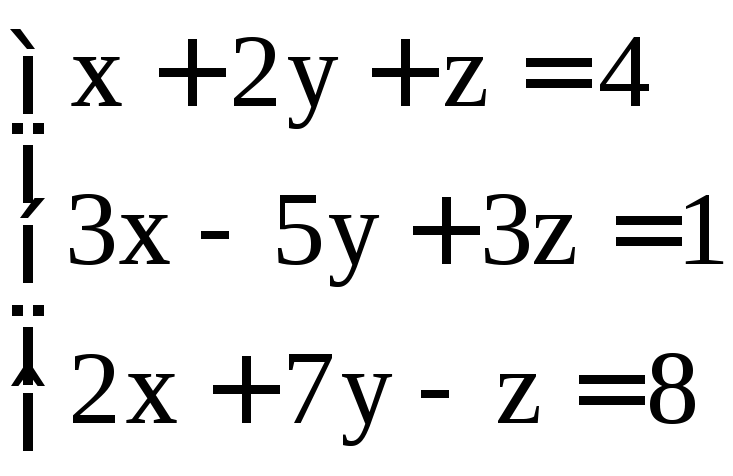 ;
;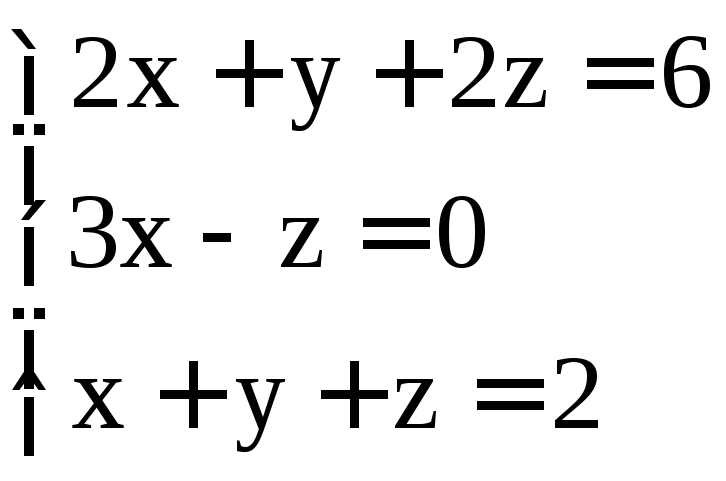 .
.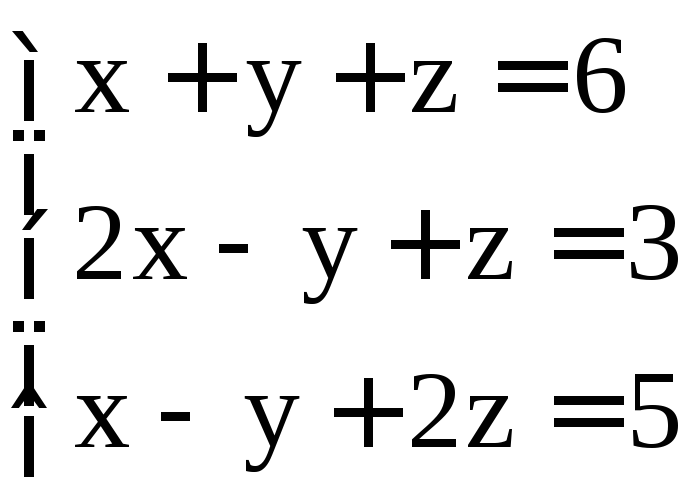 ;
;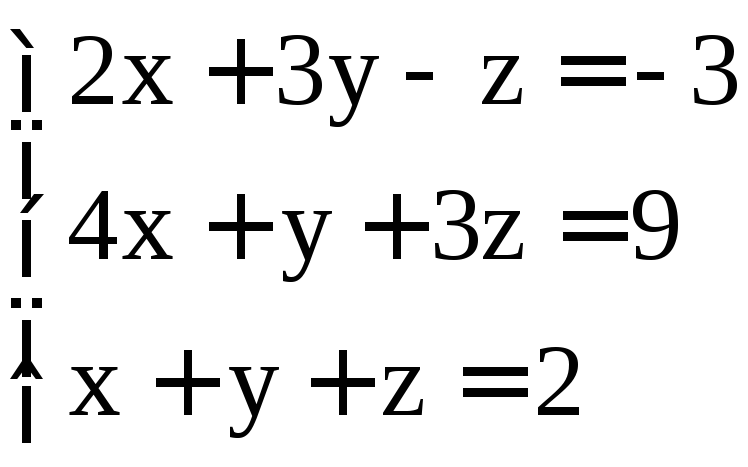 .
.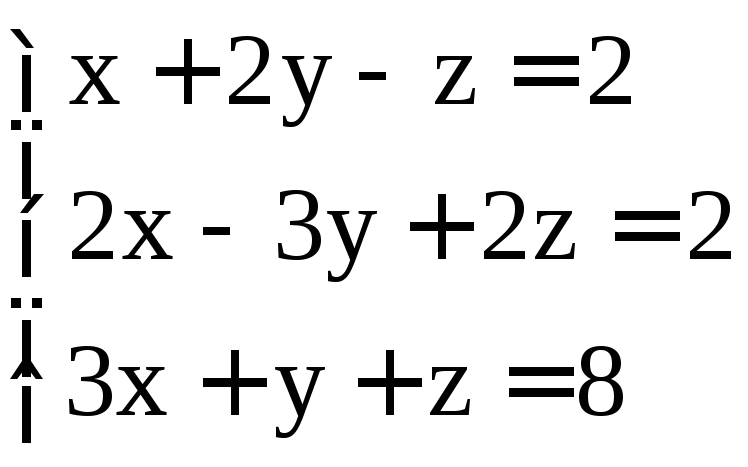 ;
;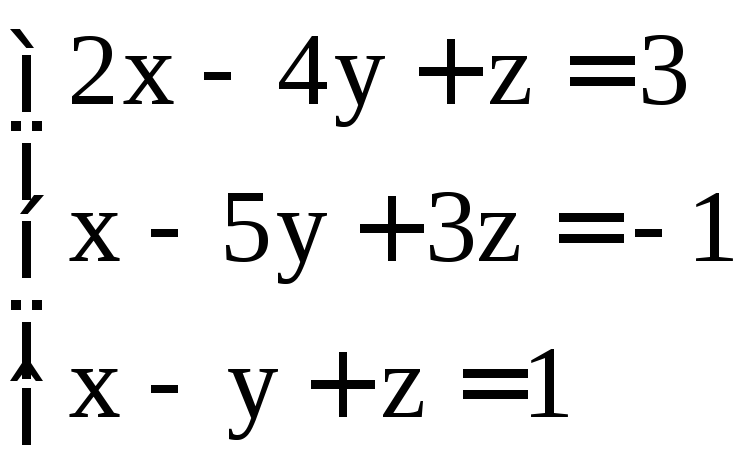 .
.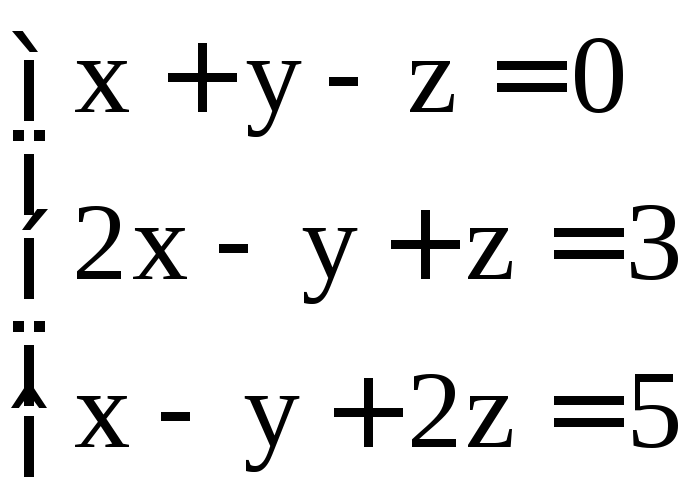 ;
; .
. ;
;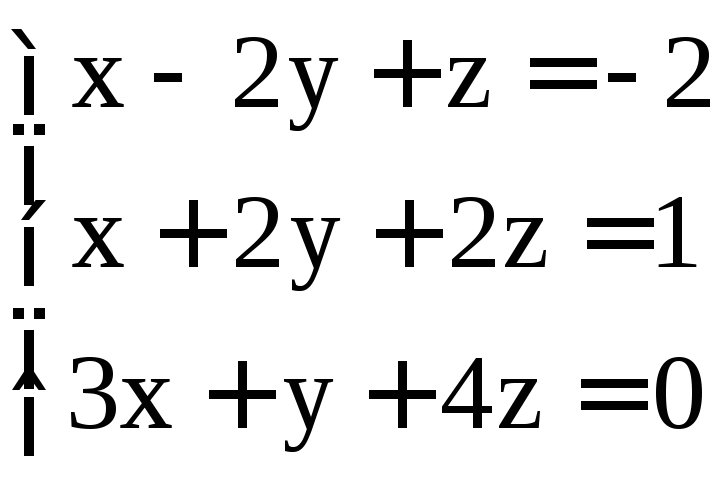 .
.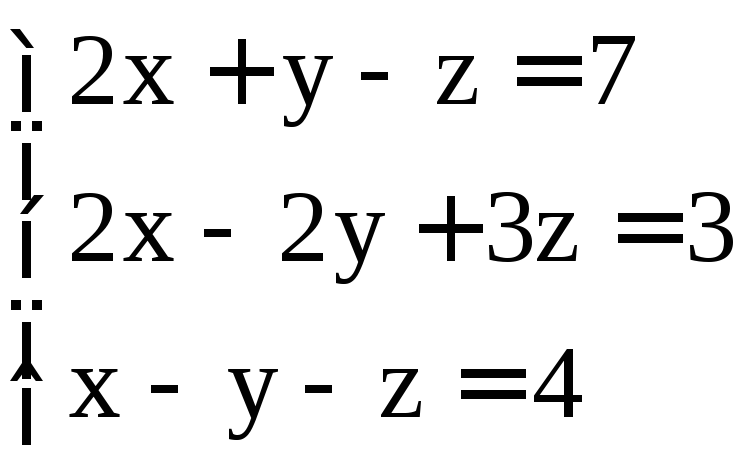 ;
;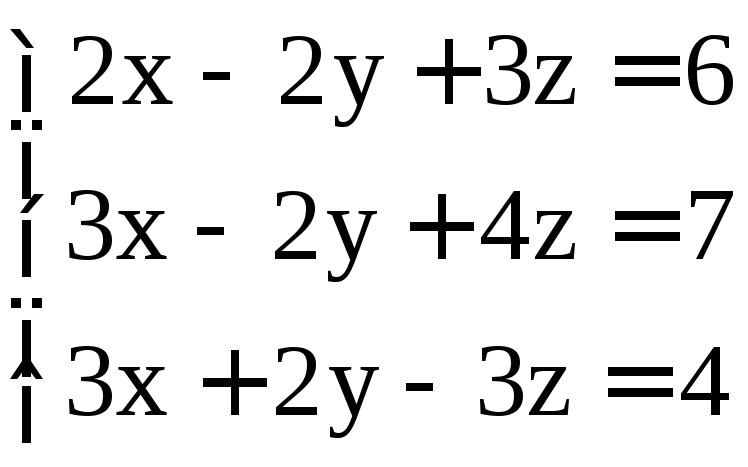 .
. ;
;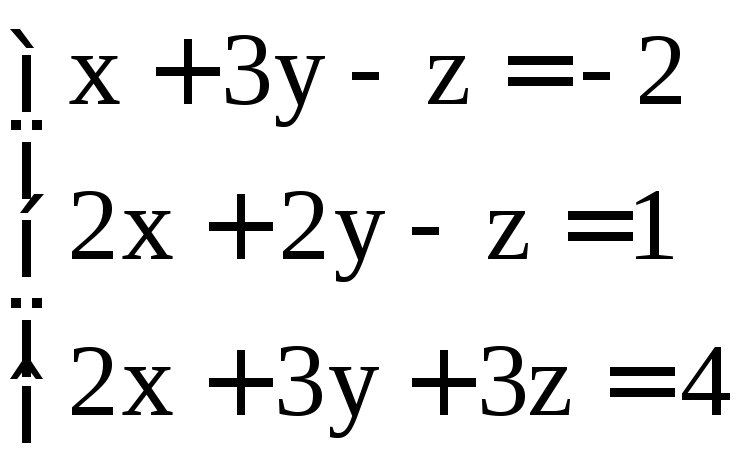 .
.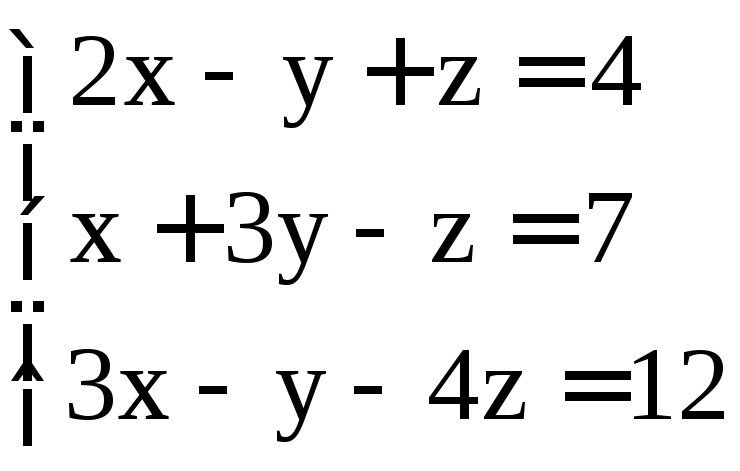 ;
;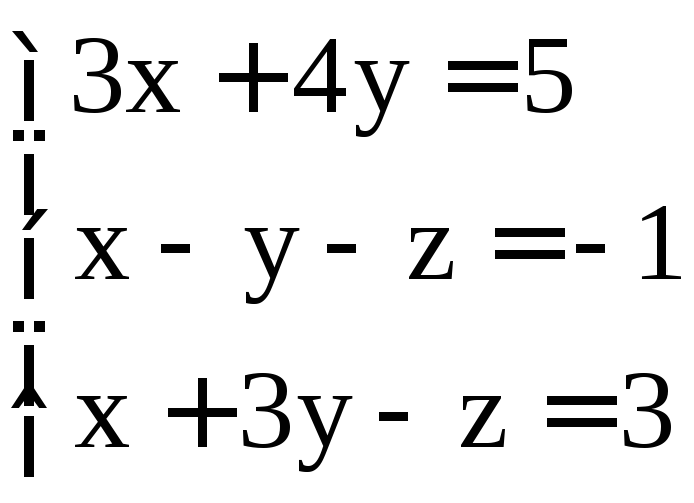 .
. ;
;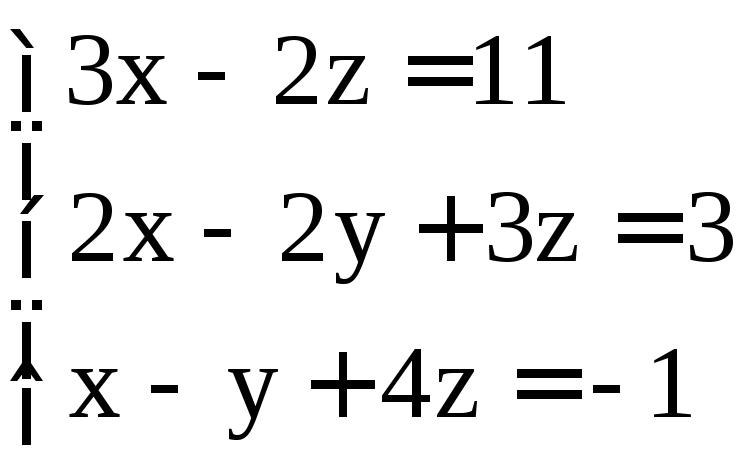 .
. ;
;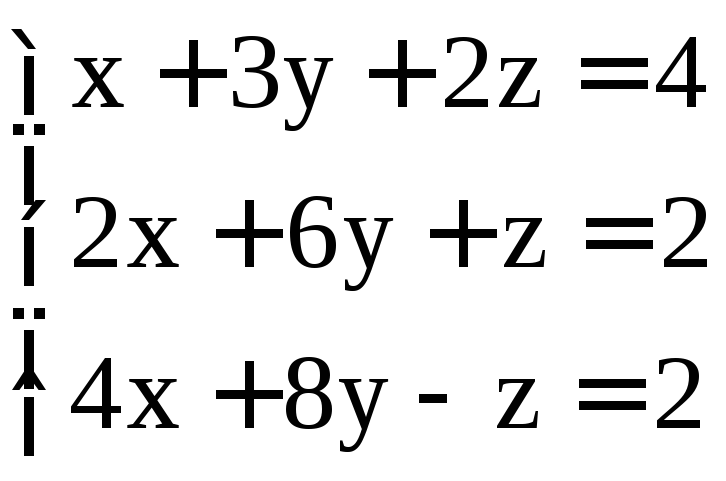 .
.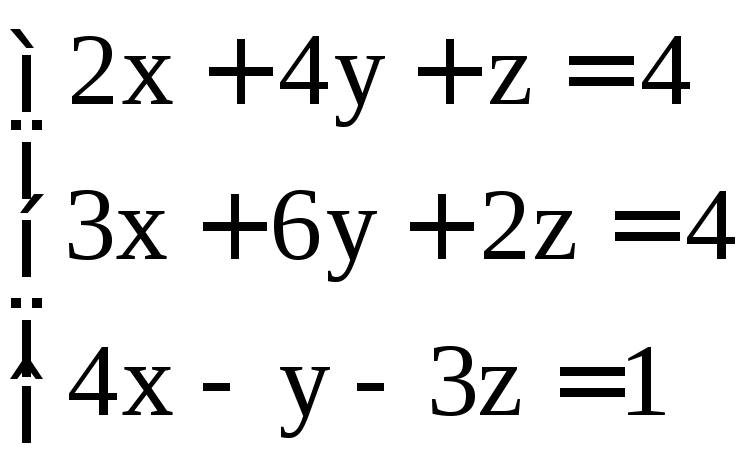 ;
;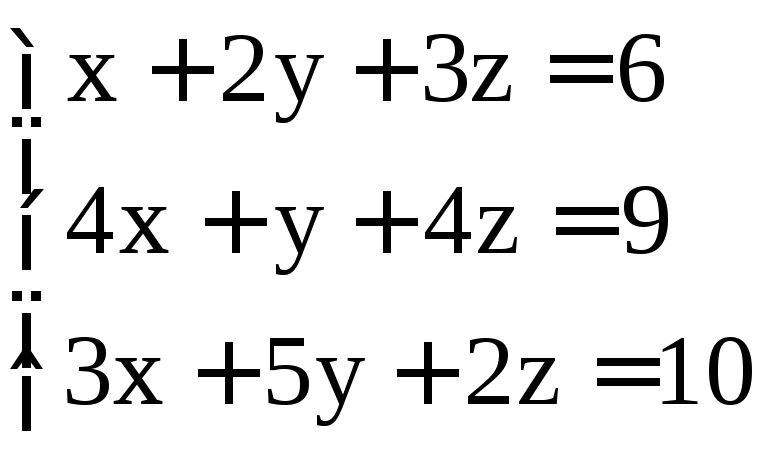 .
.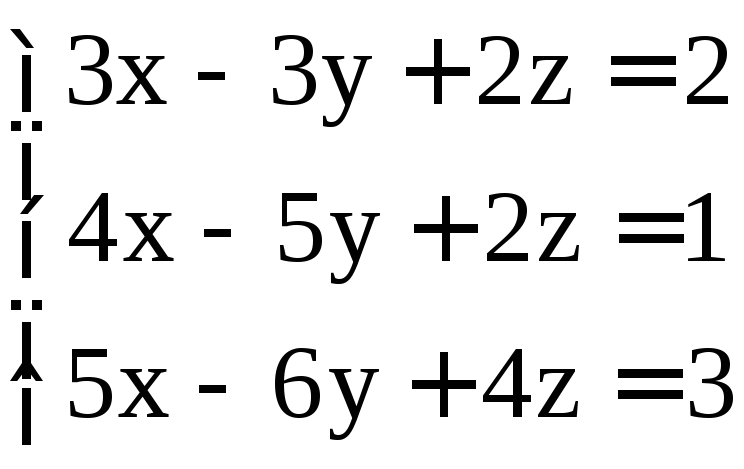 ;
;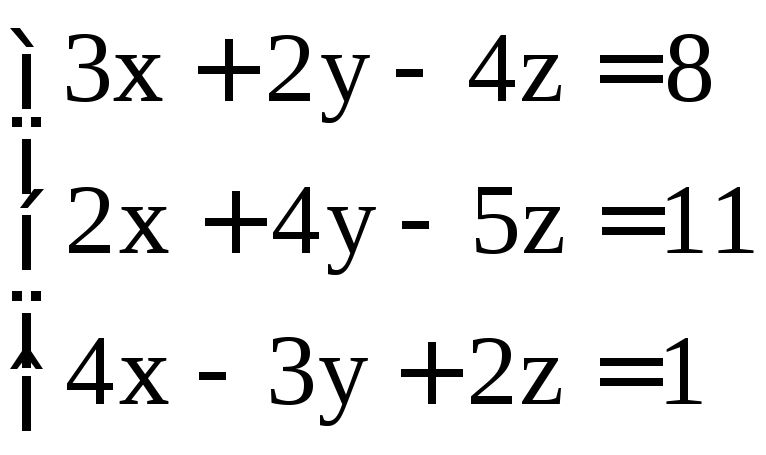 .
. ;
;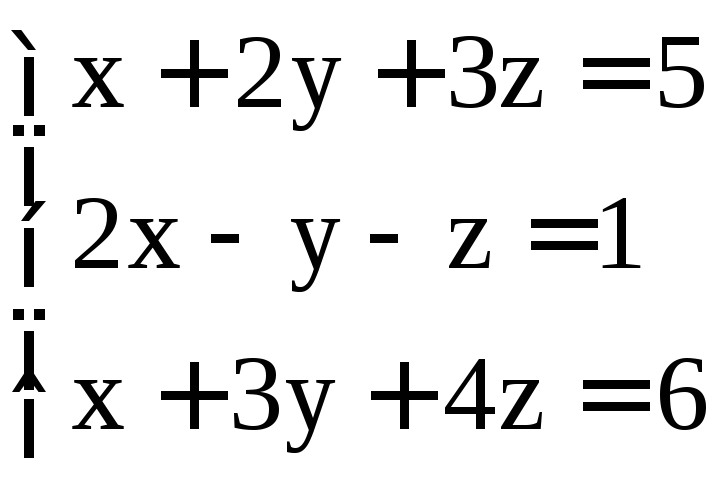 .
.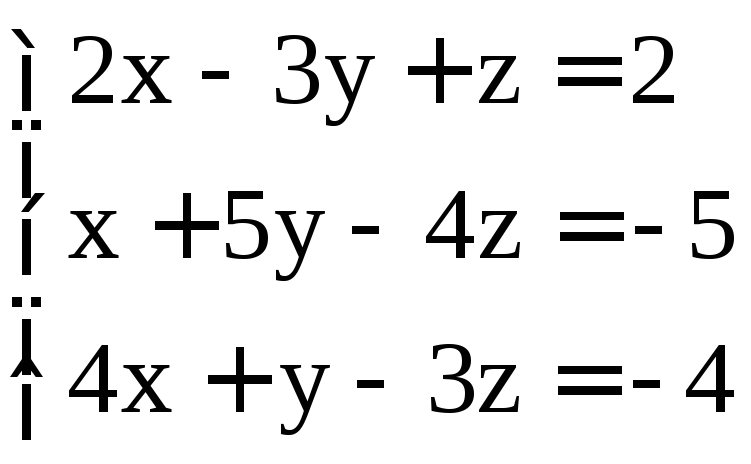 ;
;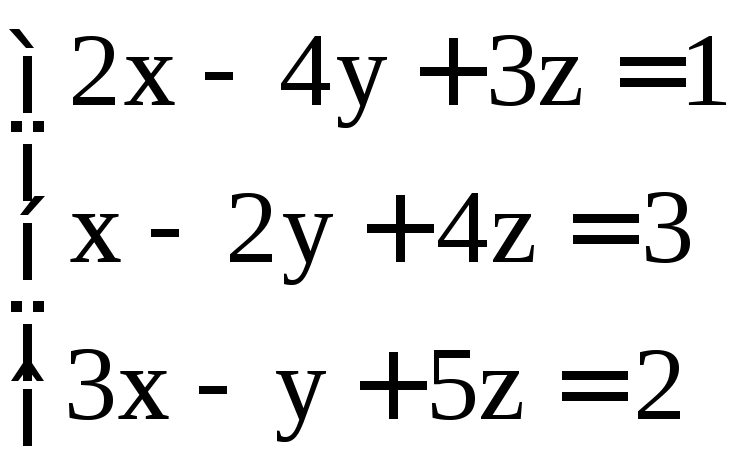 .
.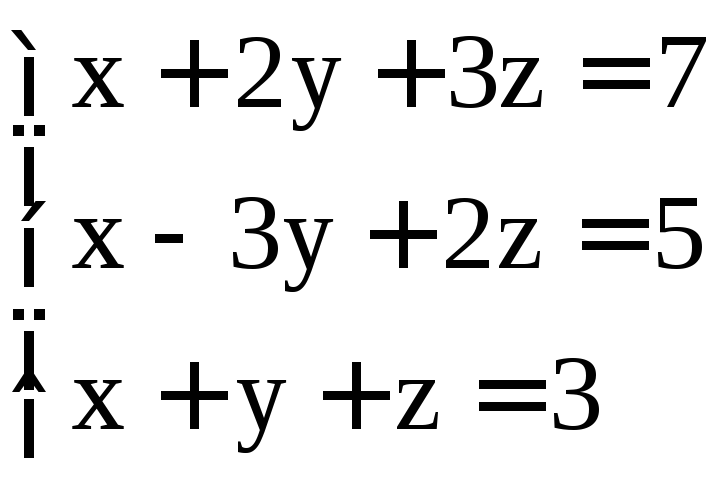 ;
;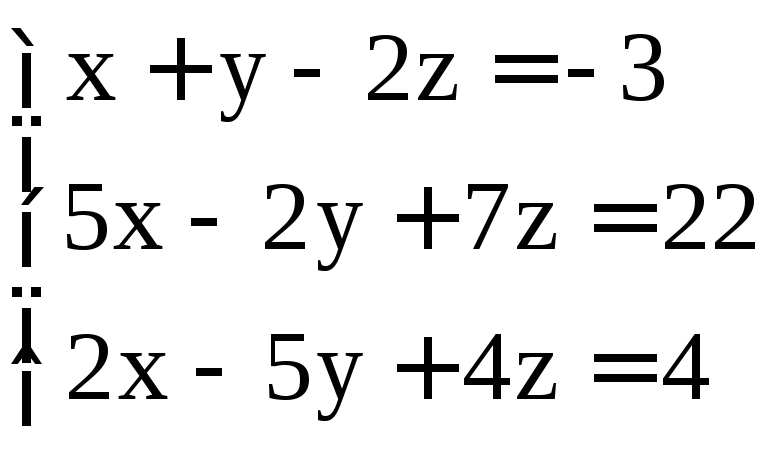 .
.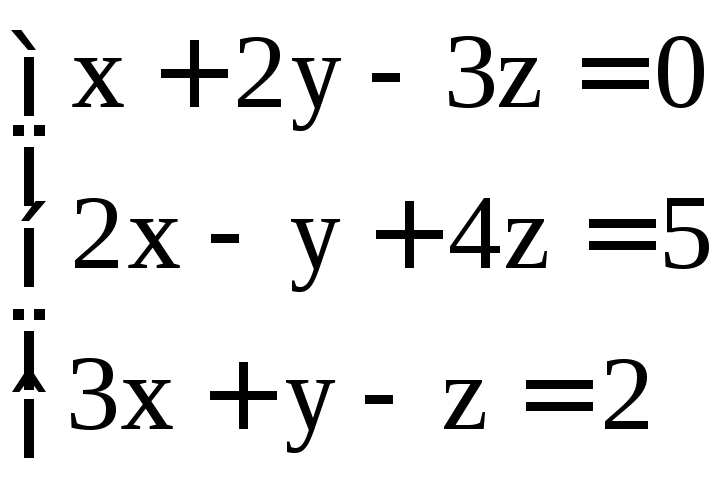 ;
; .
. ;
; .
.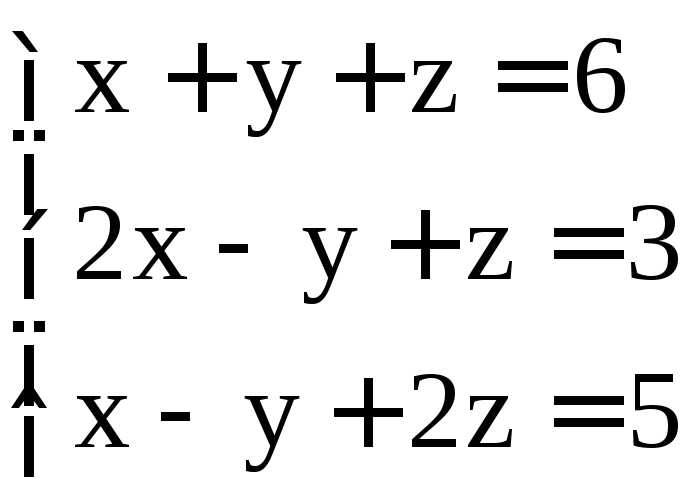 ;
;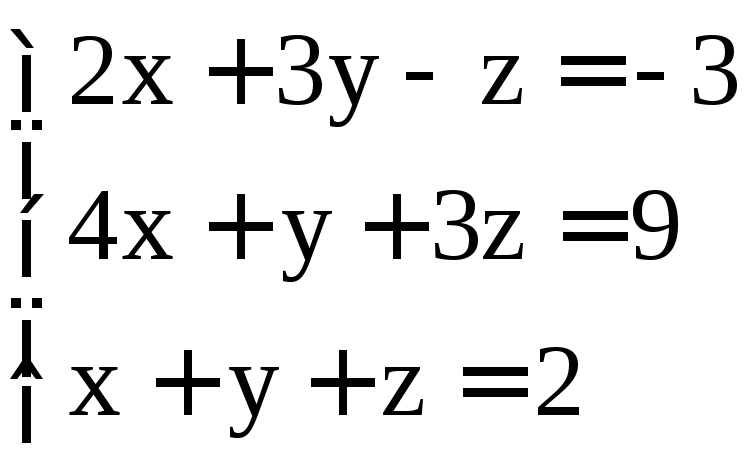 .
.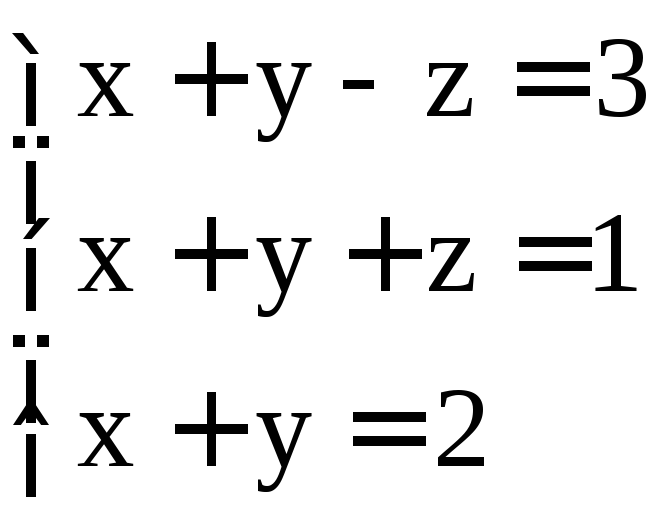 ;
; ;
; ;
;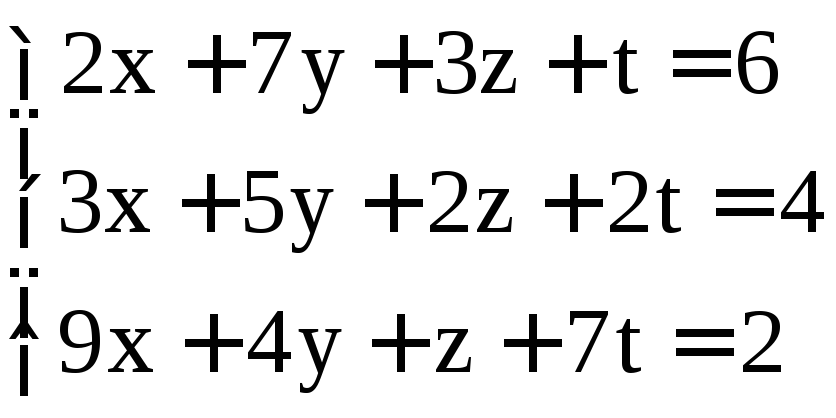 .
. ;
;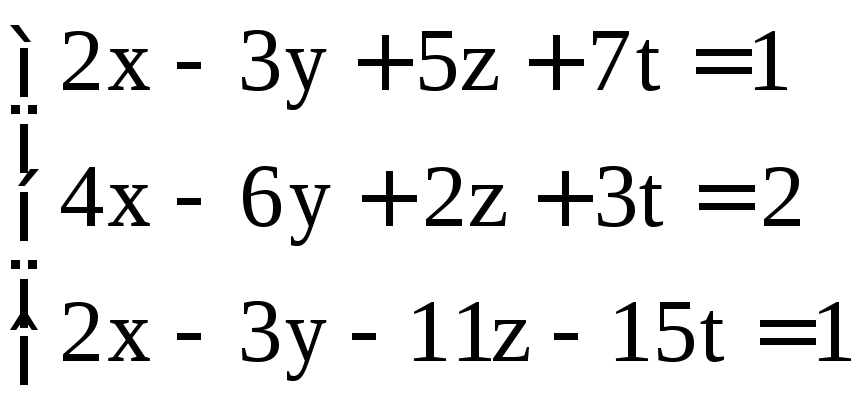 ;
;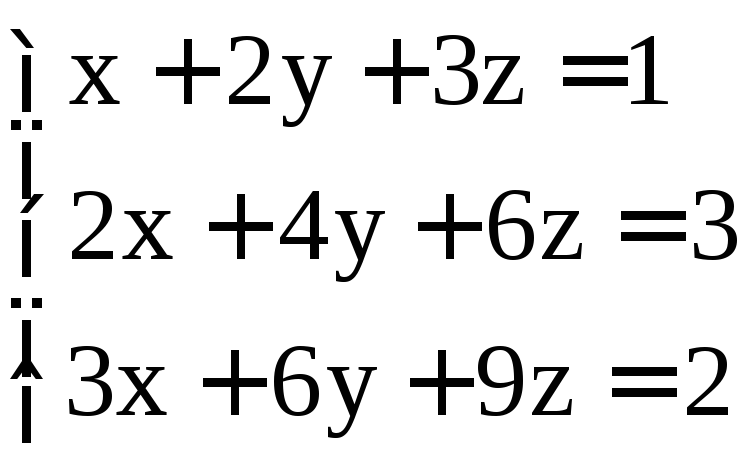 ;
;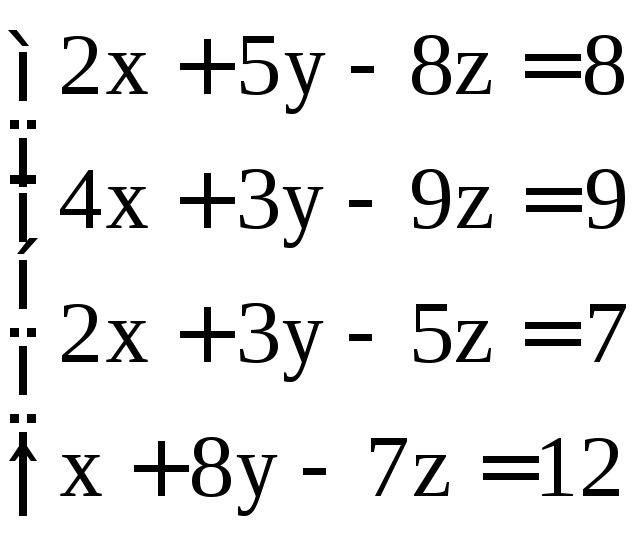 ;
;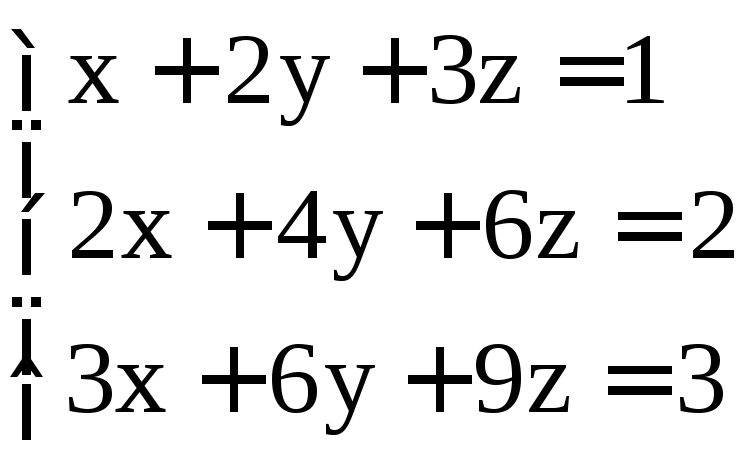 ;
; ;
;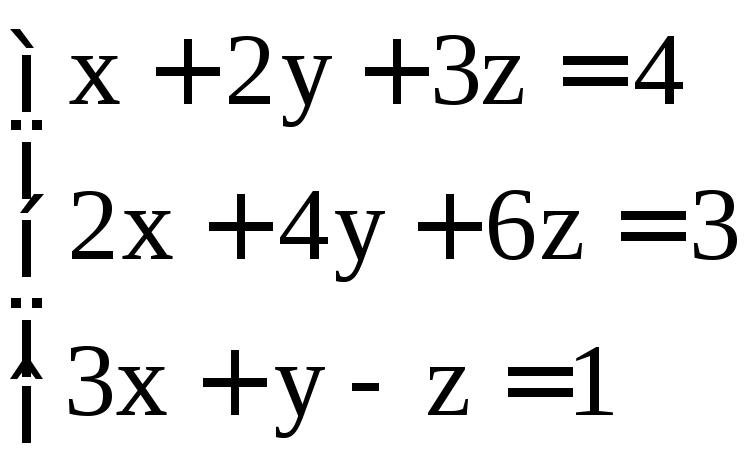 ;
; .
. ;
;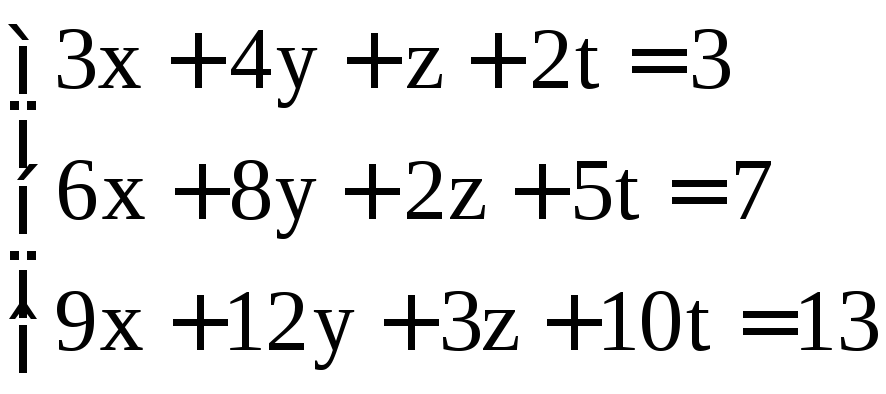 ;
;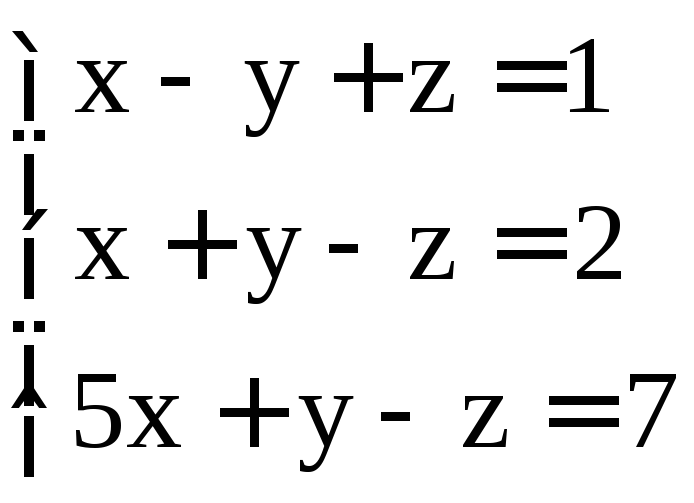 ;
;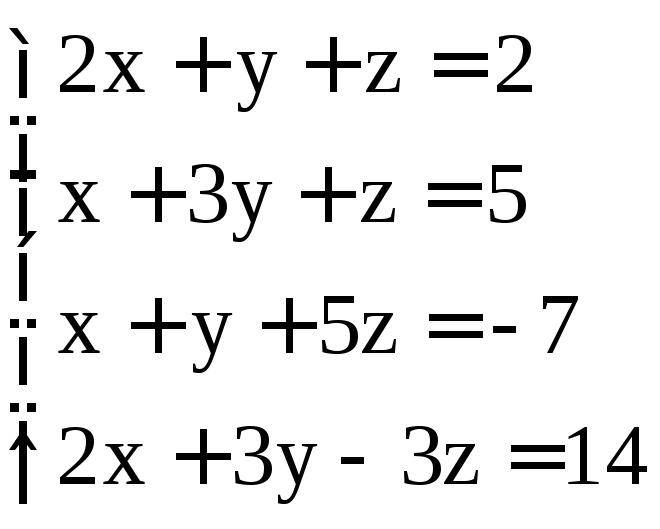 .
.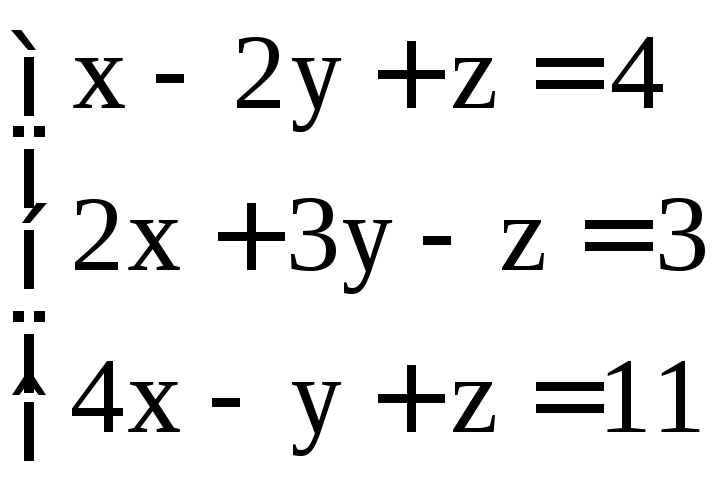 ;
;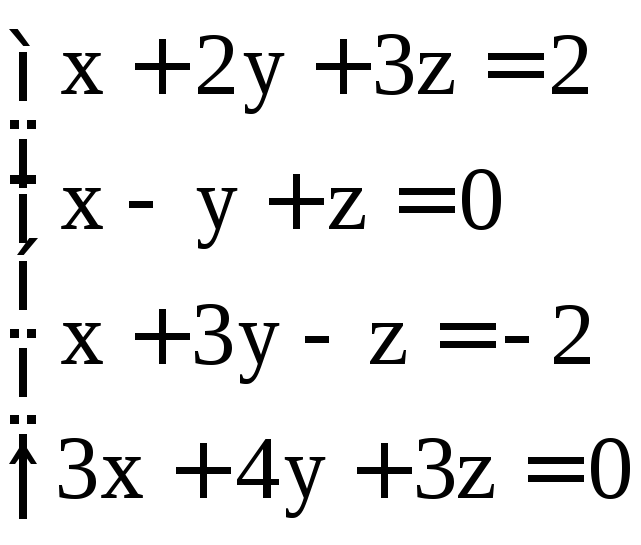 ;
;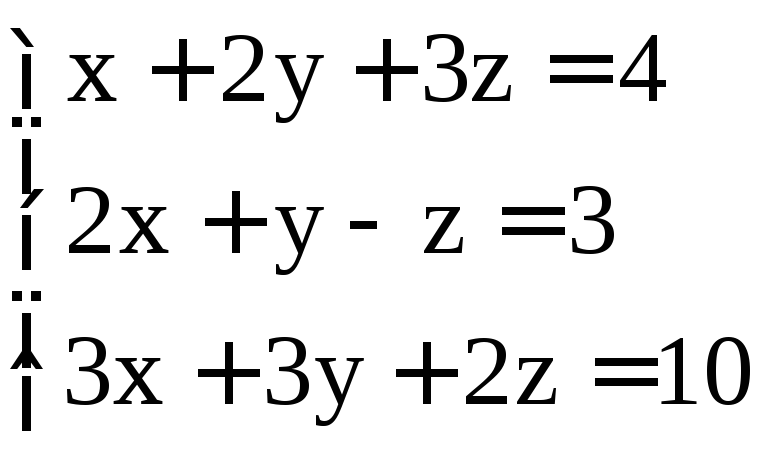 ;
;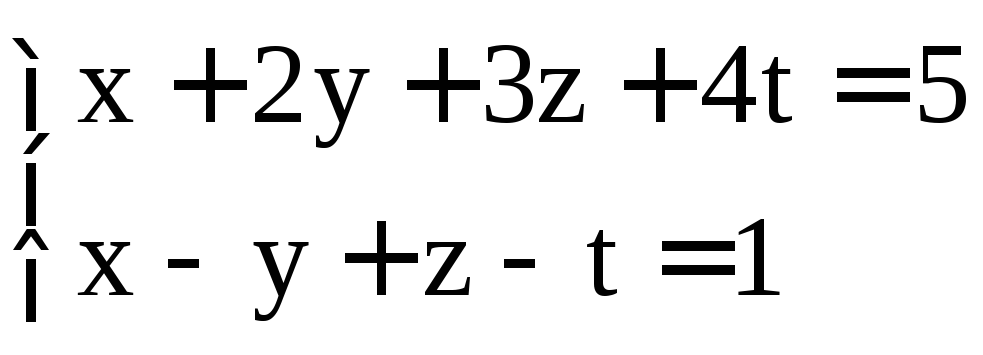 .
. ;
; ;
;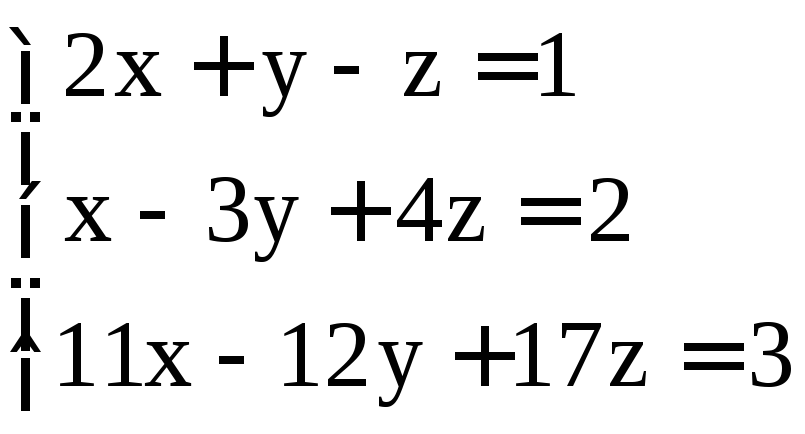 ;
;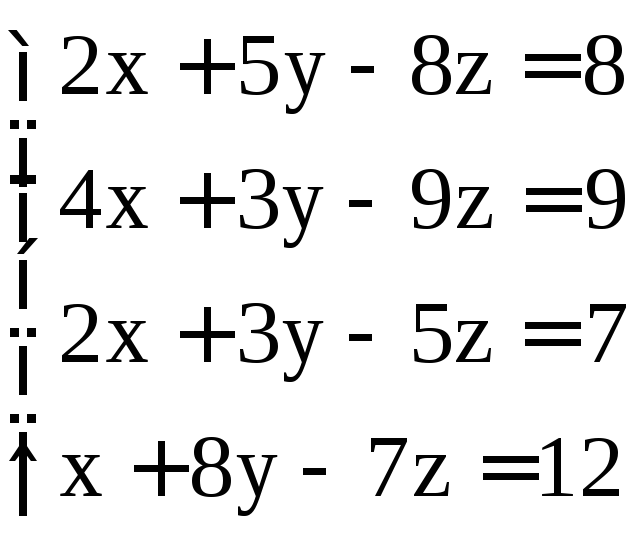 .
.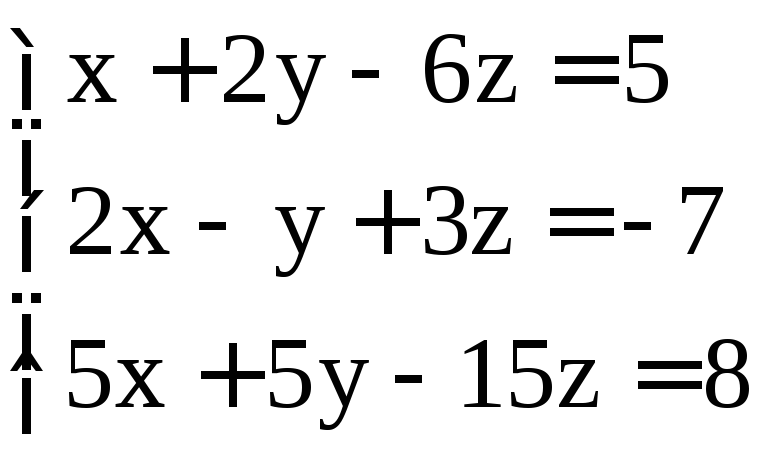 ;
;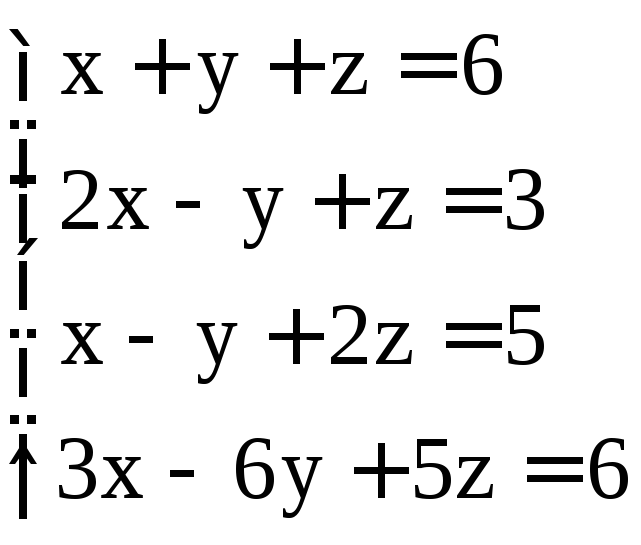 ;
; ;
;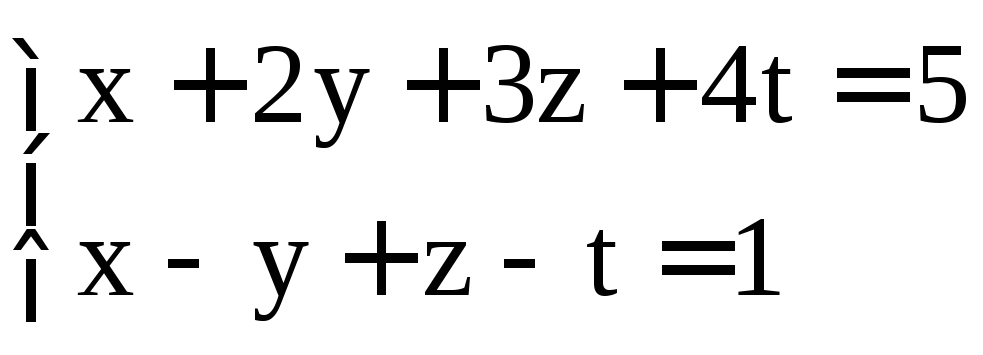 .
. ;
;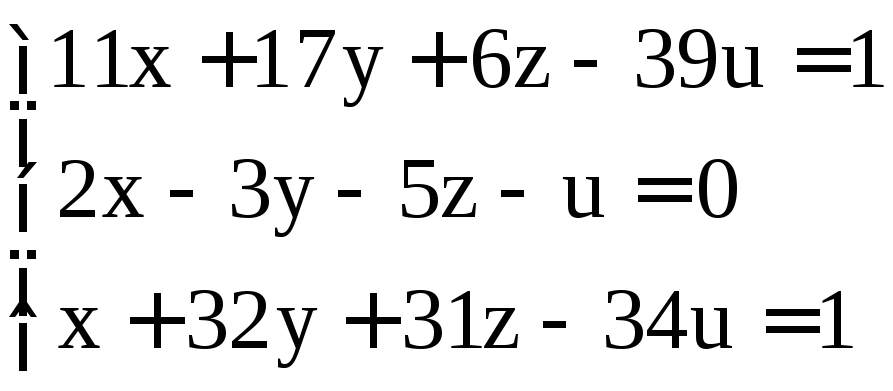 ;
; ;
; .
.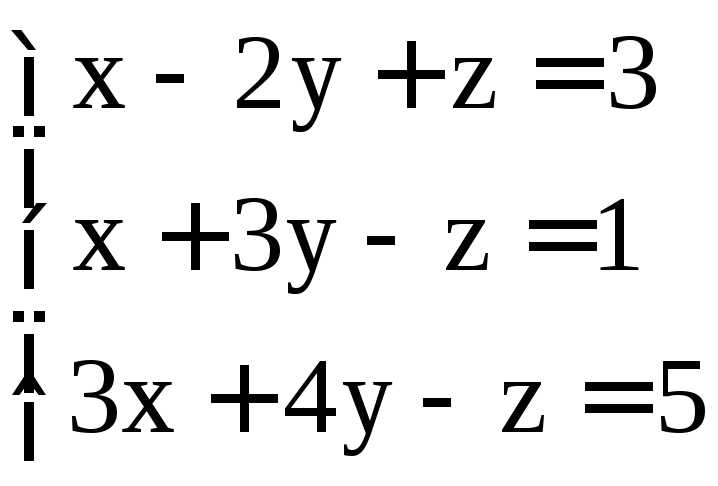 ;
;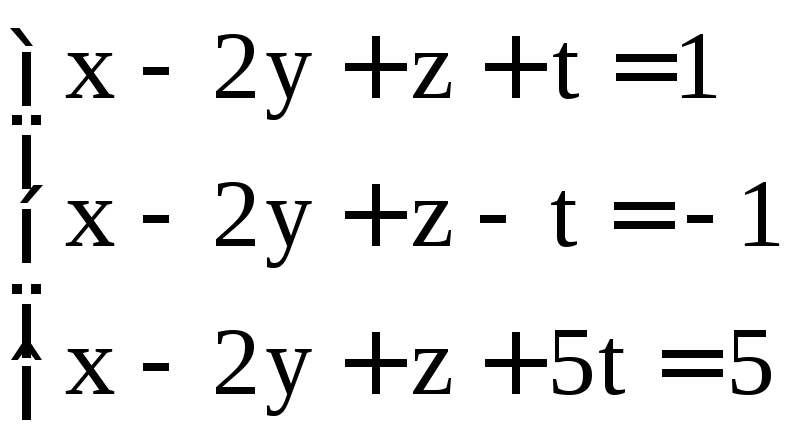 ;
;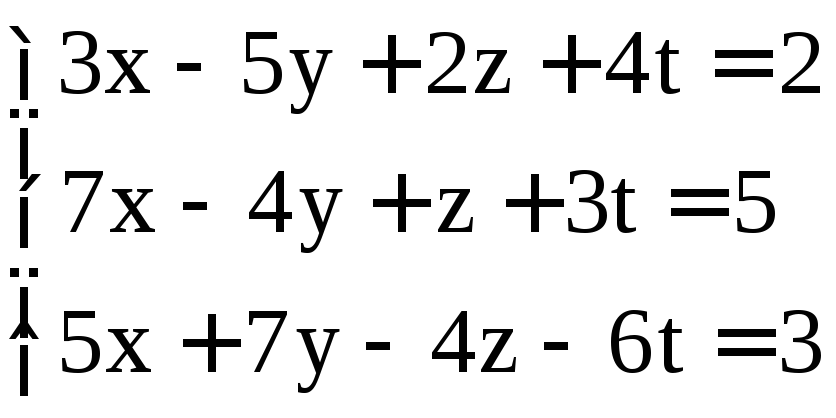 ;
;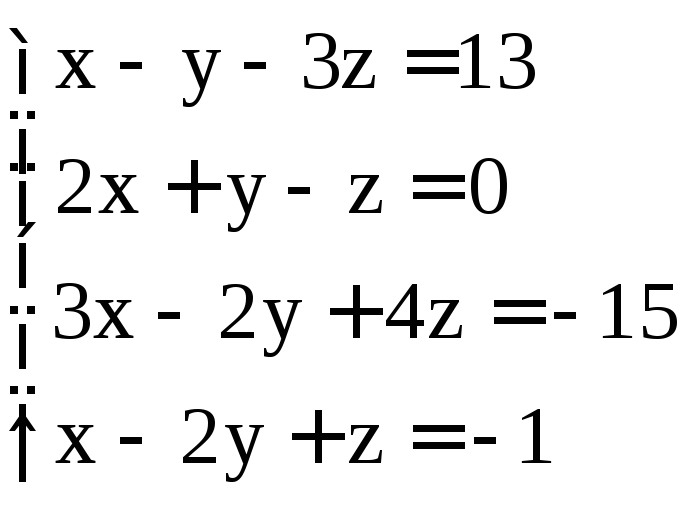 .
.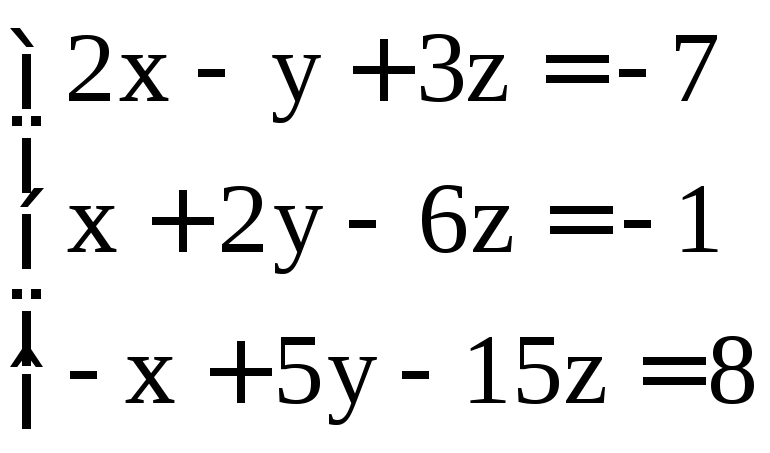 ;
;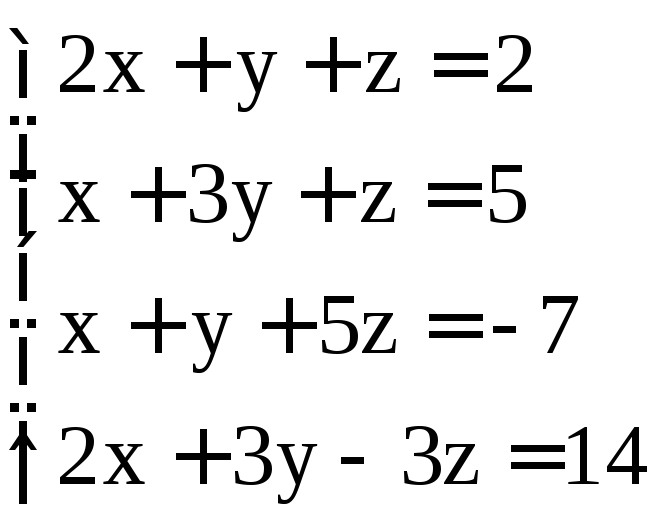 ;
;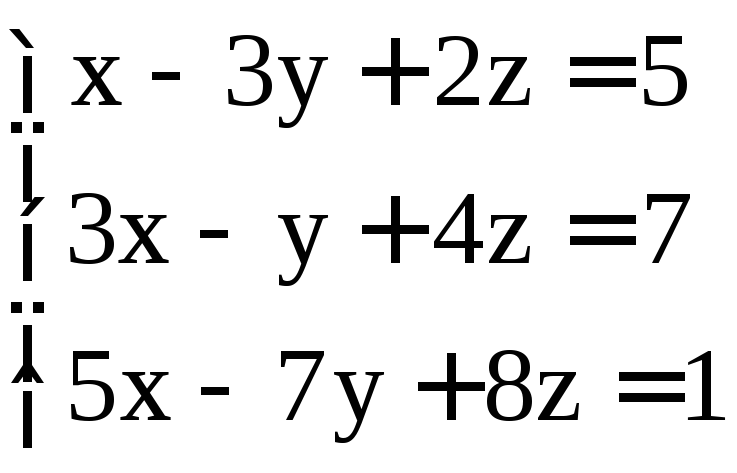 ;
;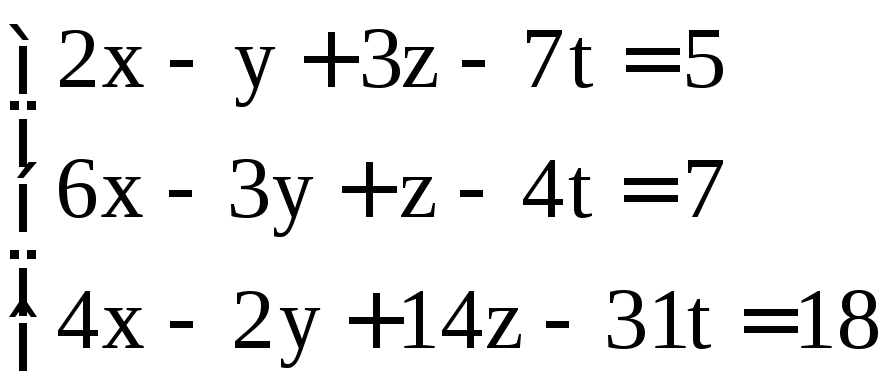 .
.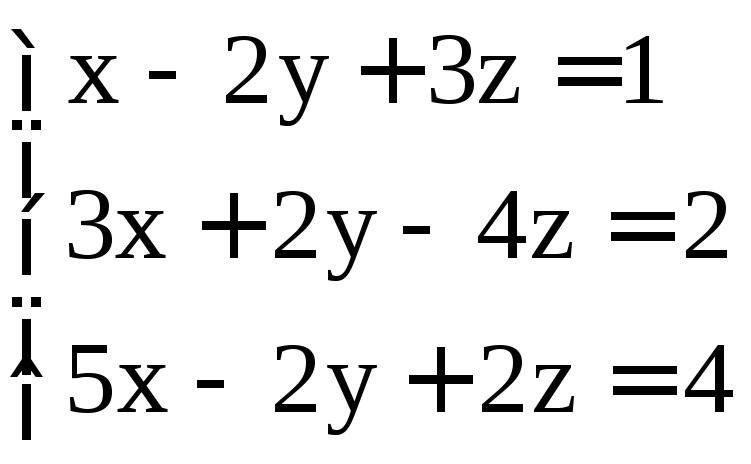 ;
; ;
;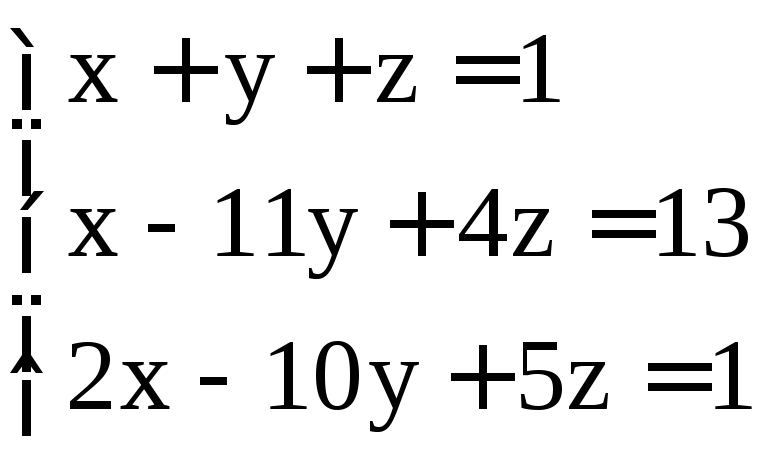 ;
;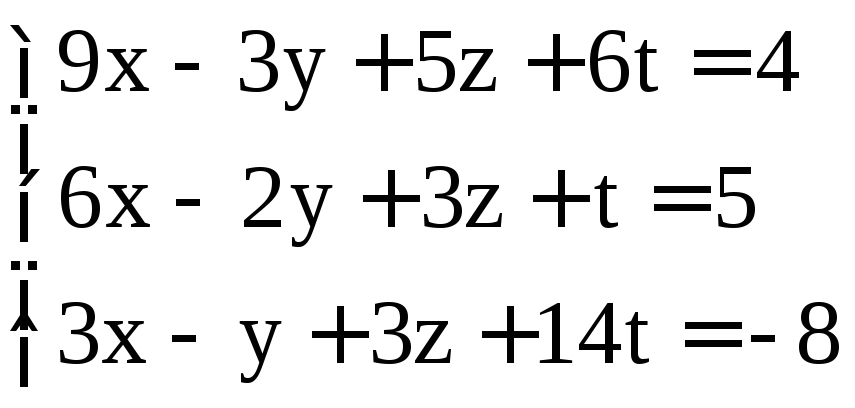 .
.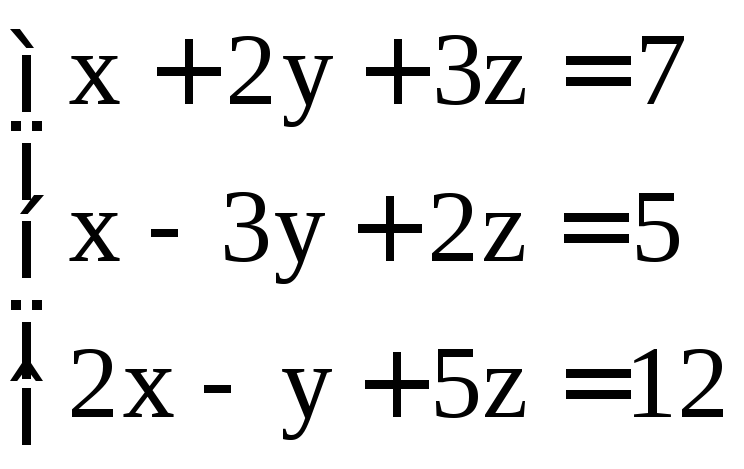 ;
;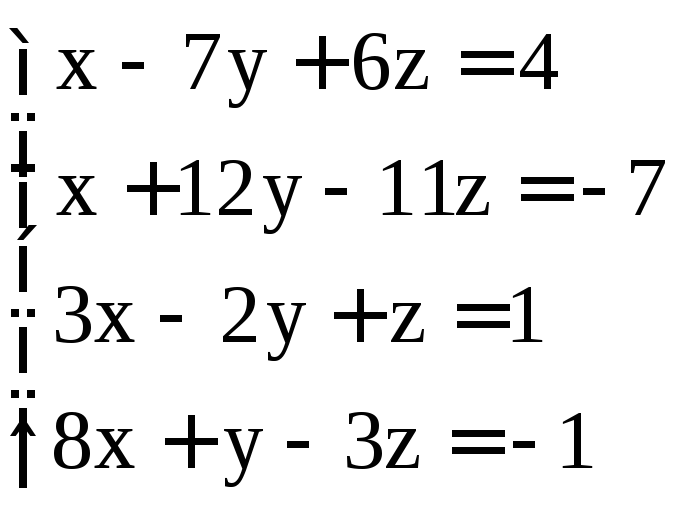 ;
; ;
;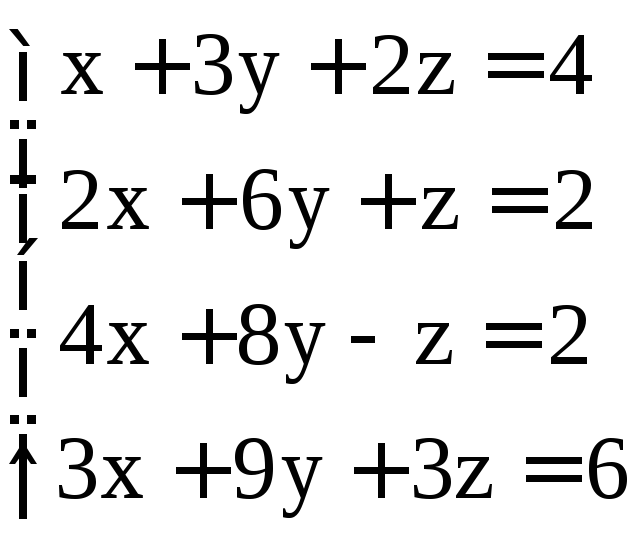 .
.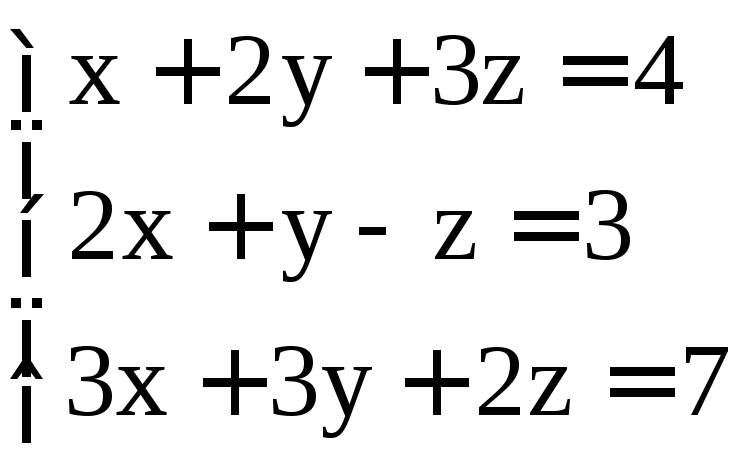 ;
; ;
;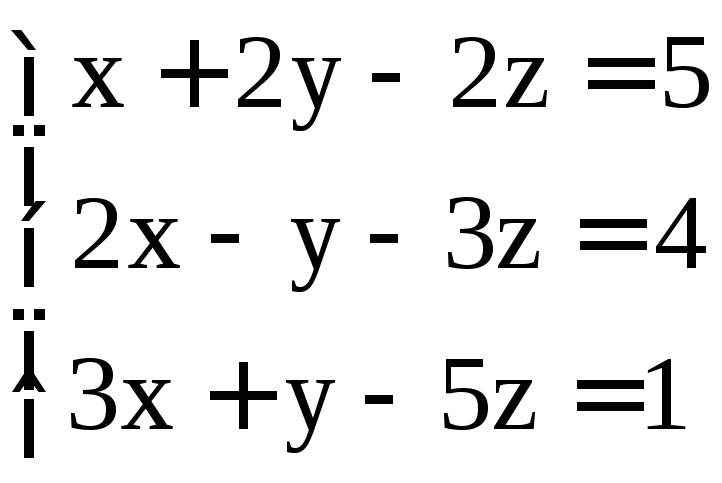 ;
;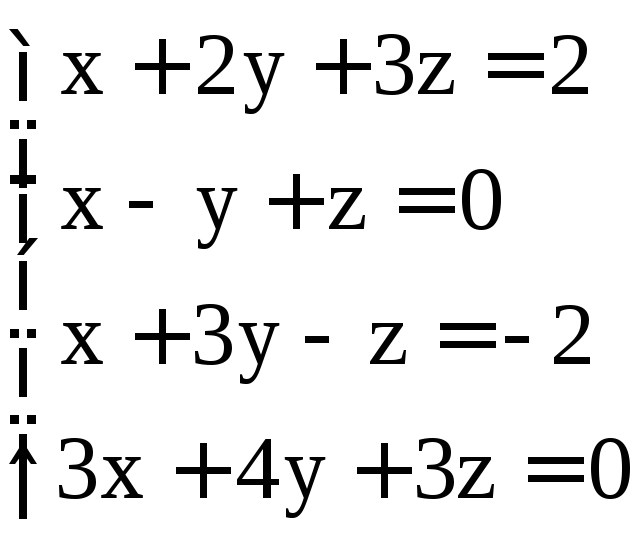 .
.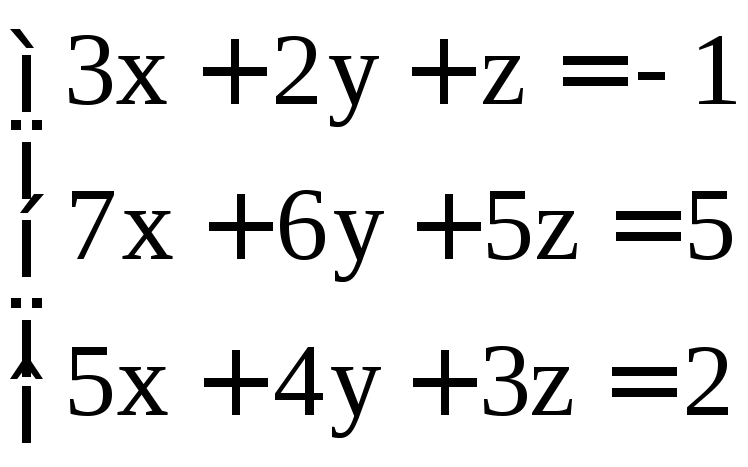 ;
; ;
;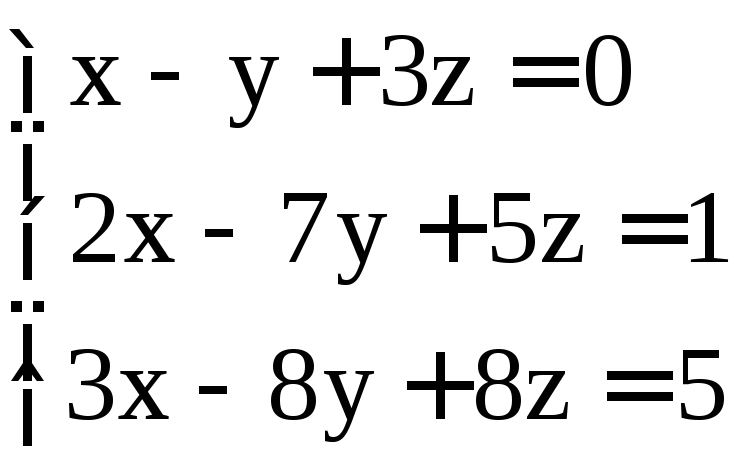 ;
;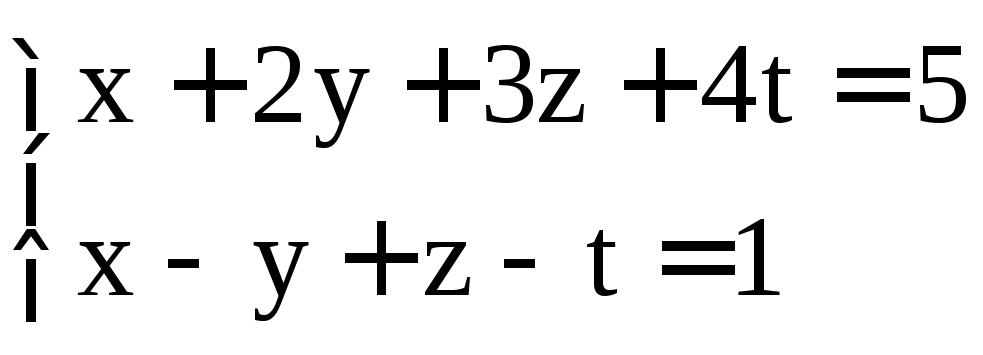 .
. ;
;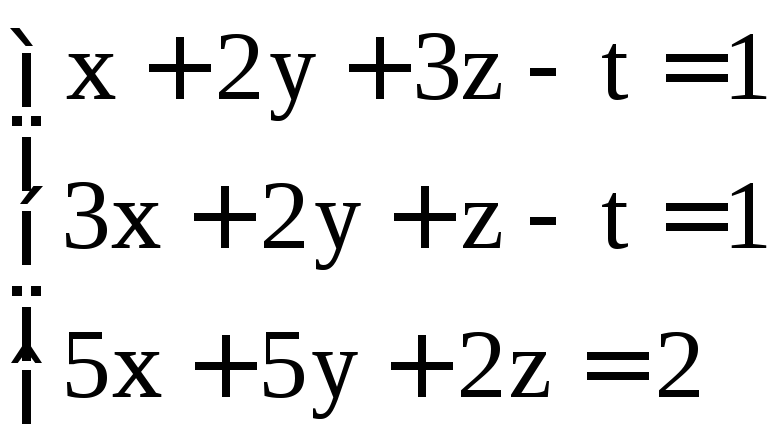 ;
; ;
; .
. ;
; ;
; ;
;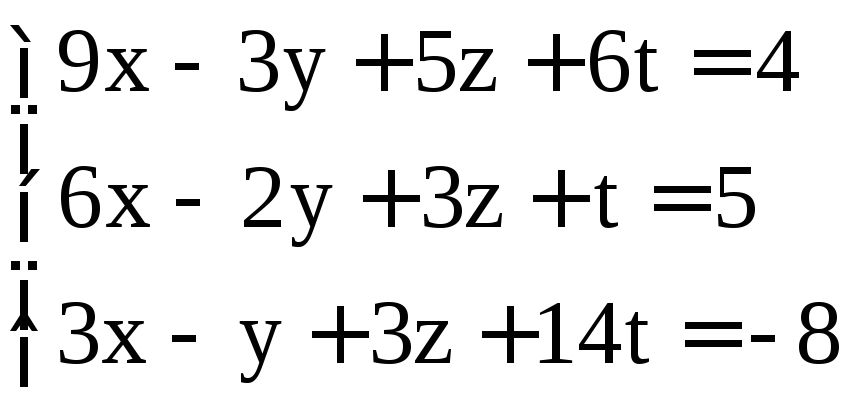 .
.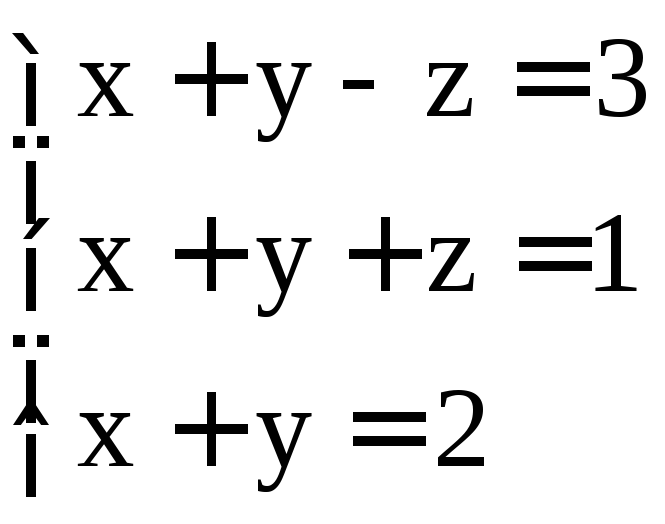 ;
;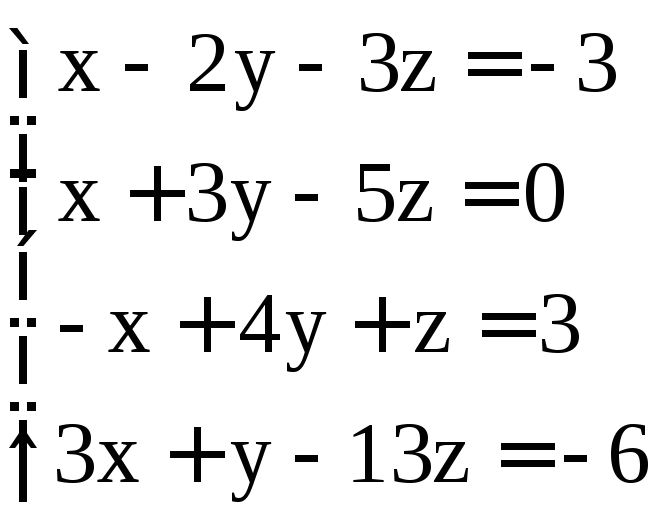 ;
;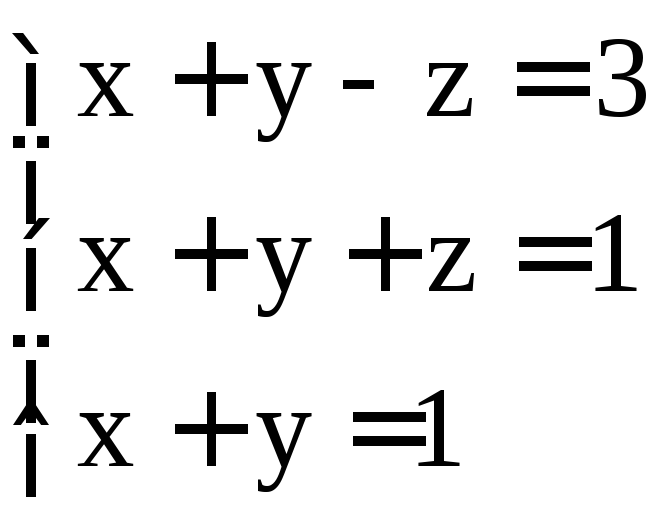 ;
;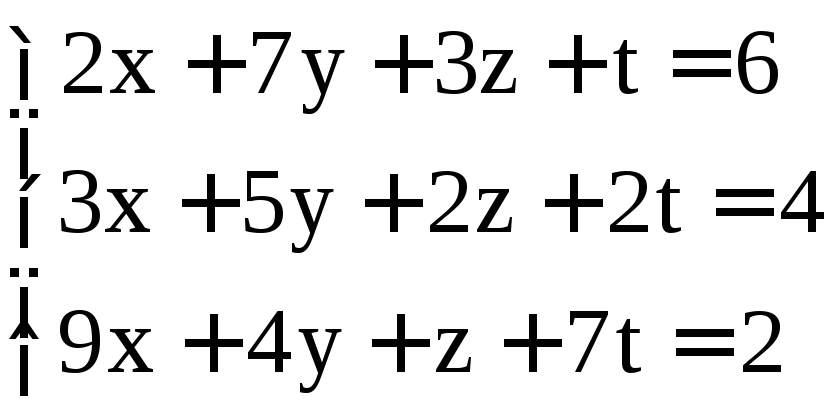 .
.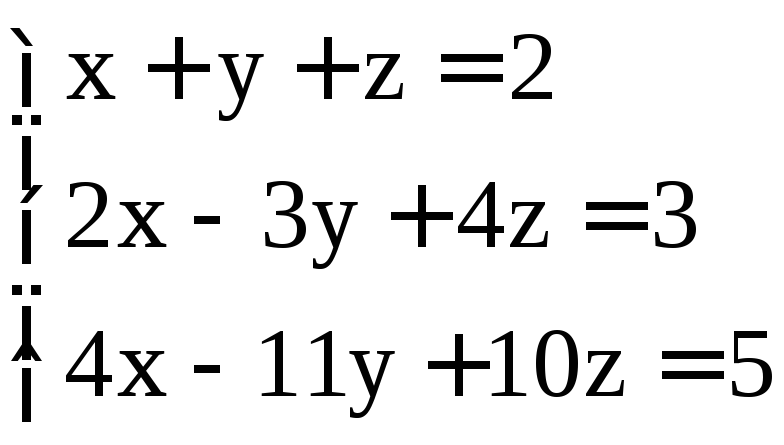 ;
; ;
;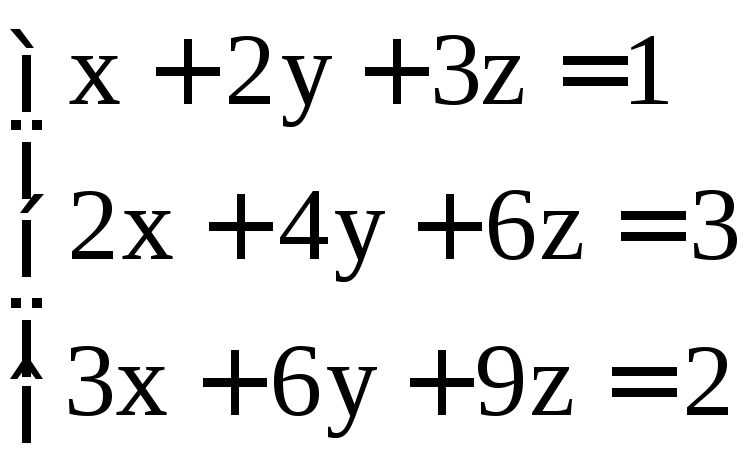 ;
;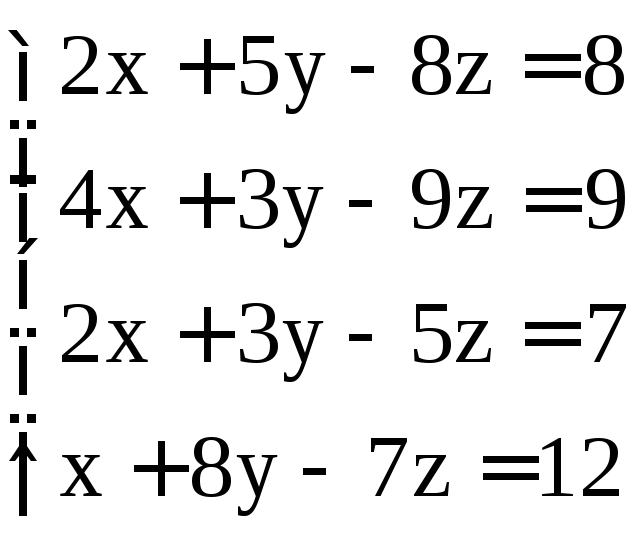 ;
;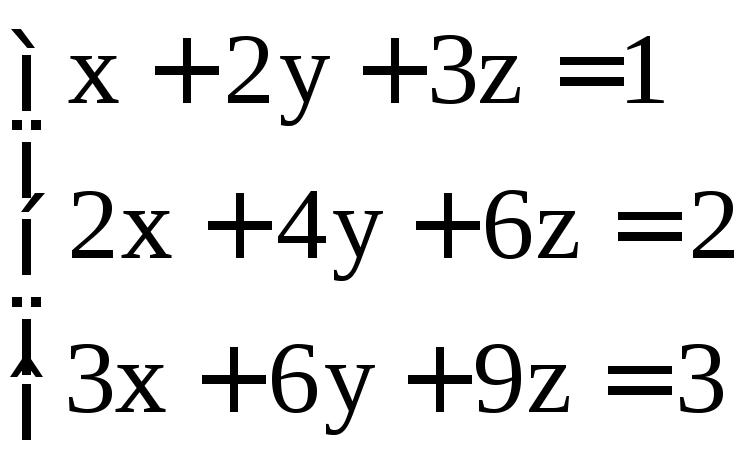 ;
;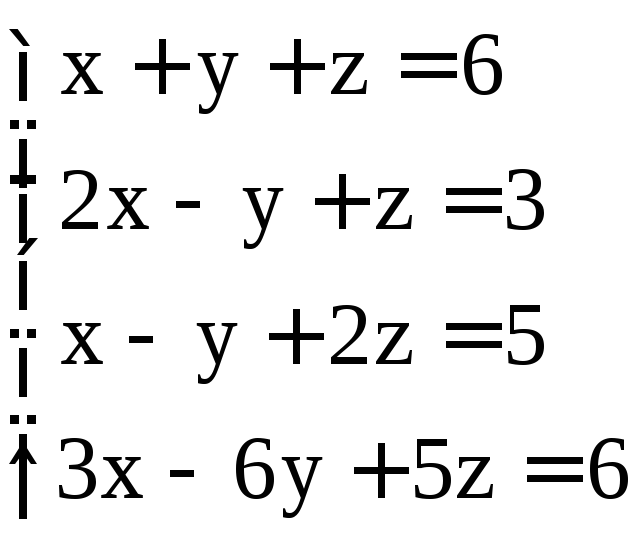 ;
;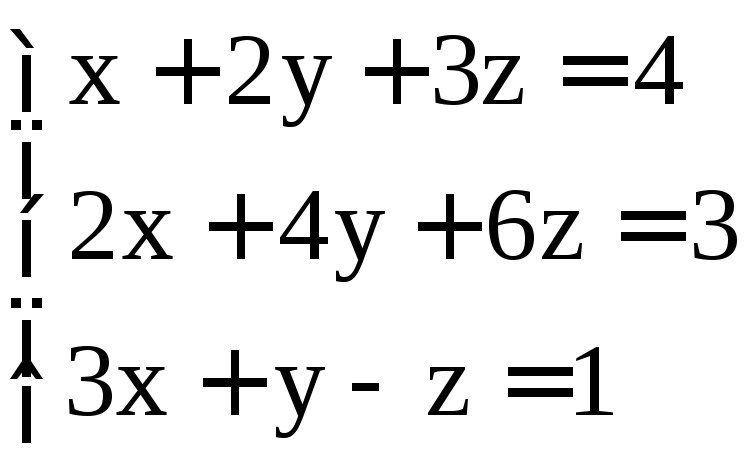 ;
;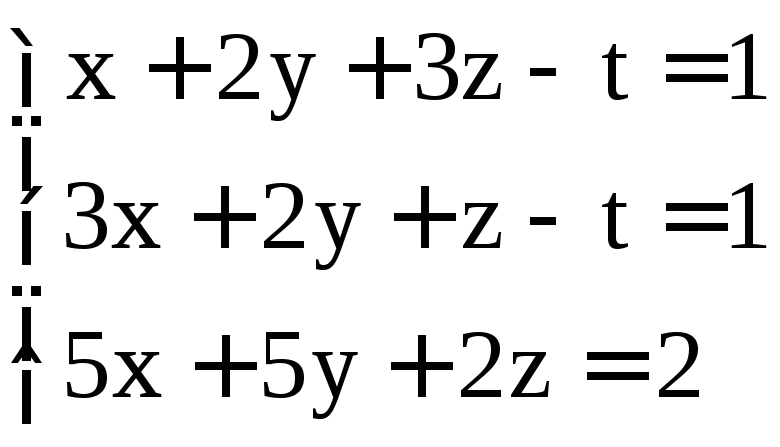 .
.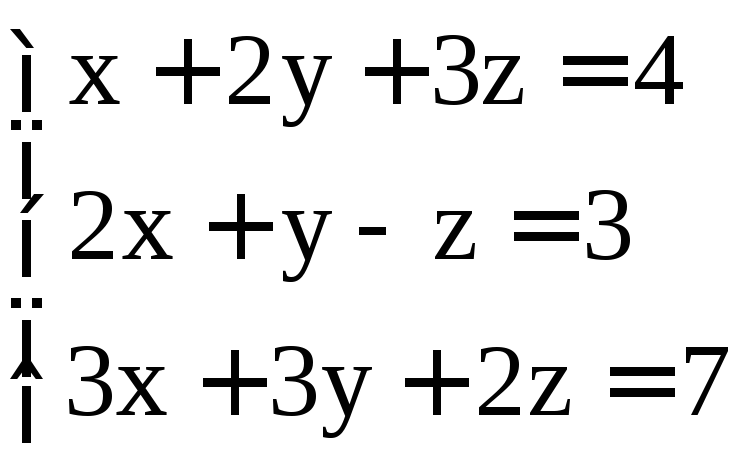 ;
;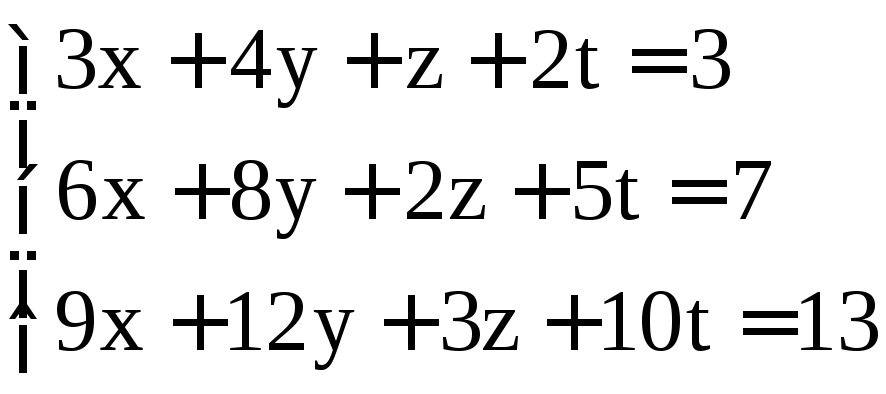 ;
; ;
;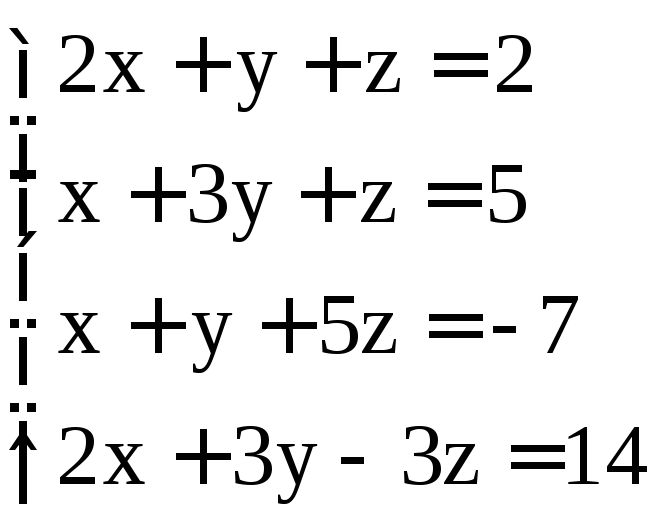 .
.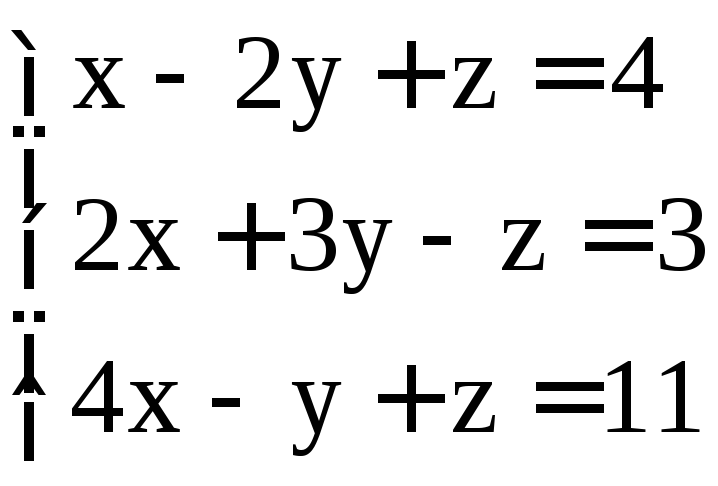 ;
;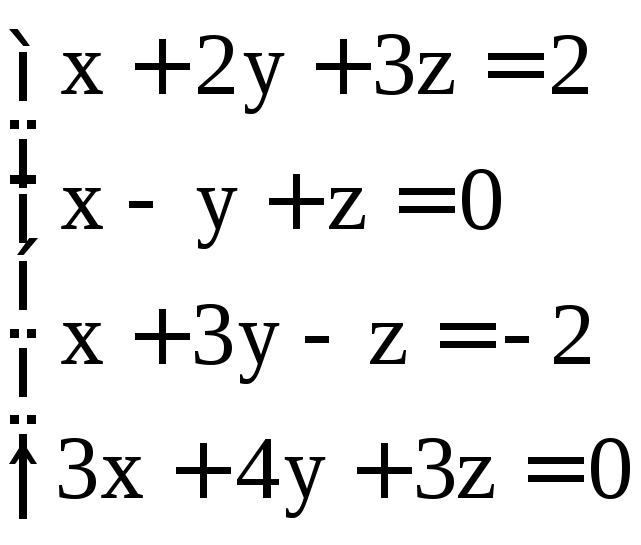 ;
;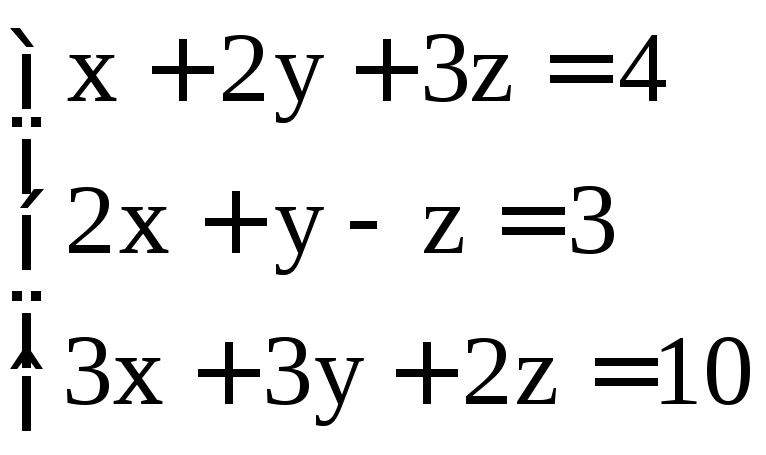 ;
;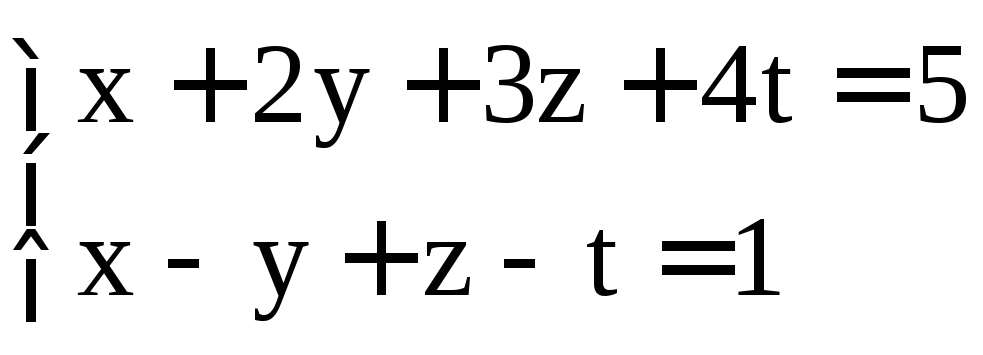 .
.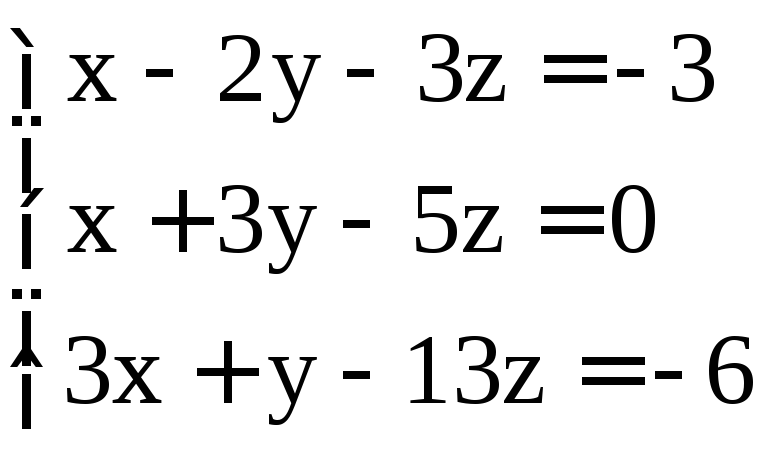 ;
; ;
; ;
;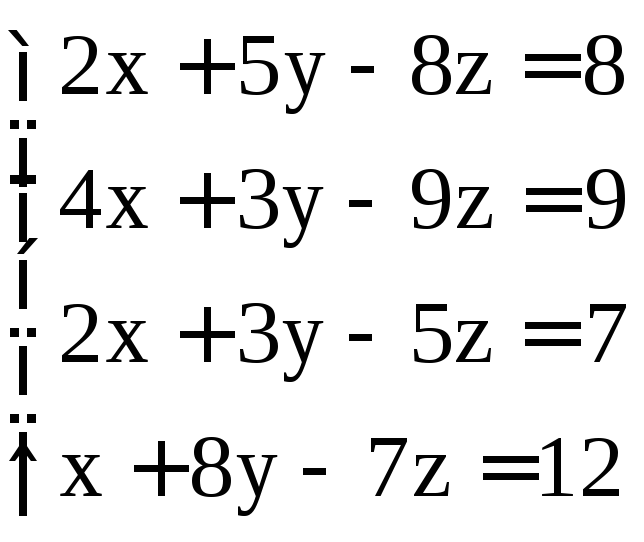 .
.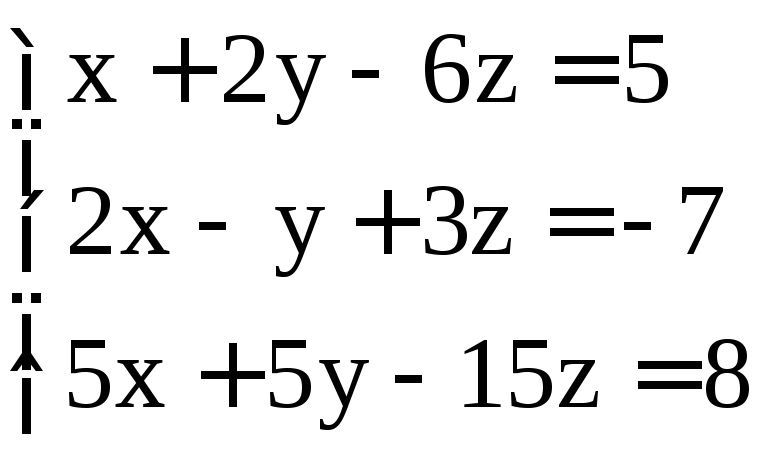 ;
; ;
;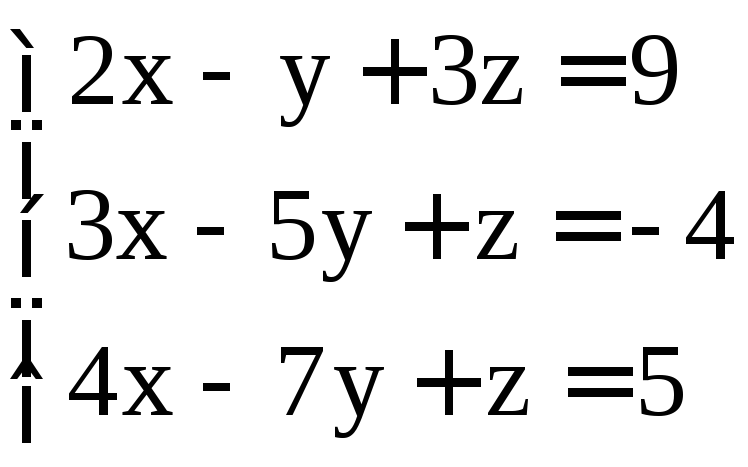 ;
; .
.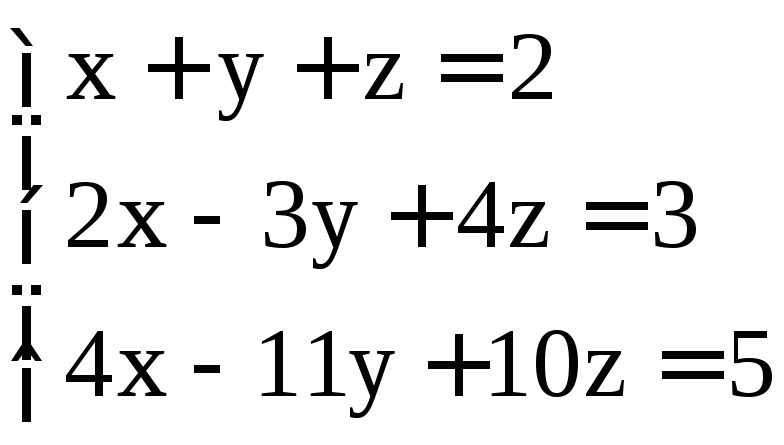 ;
; ;
;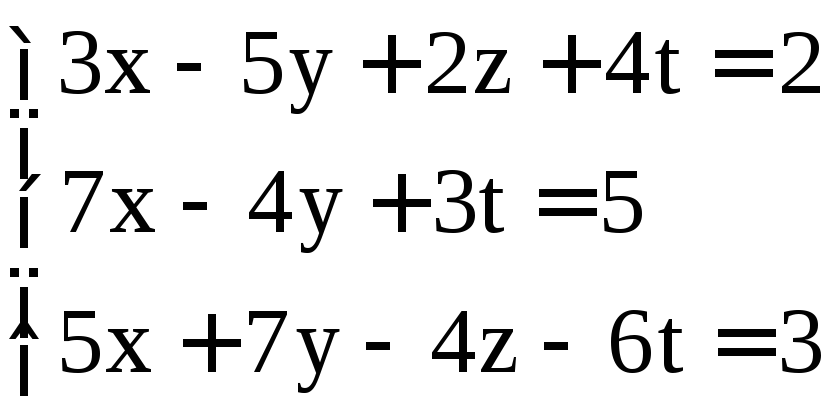 ;
;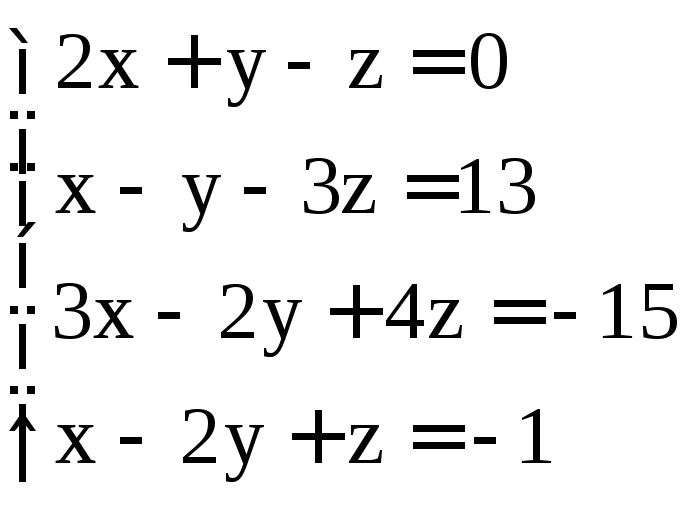 .
. ;
;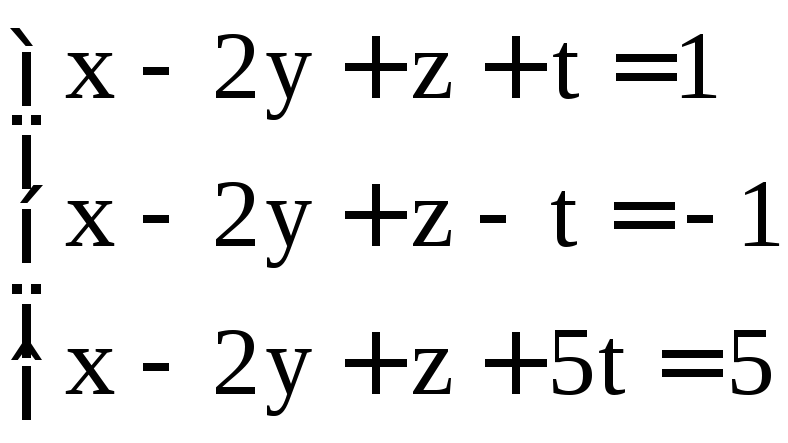 ;
;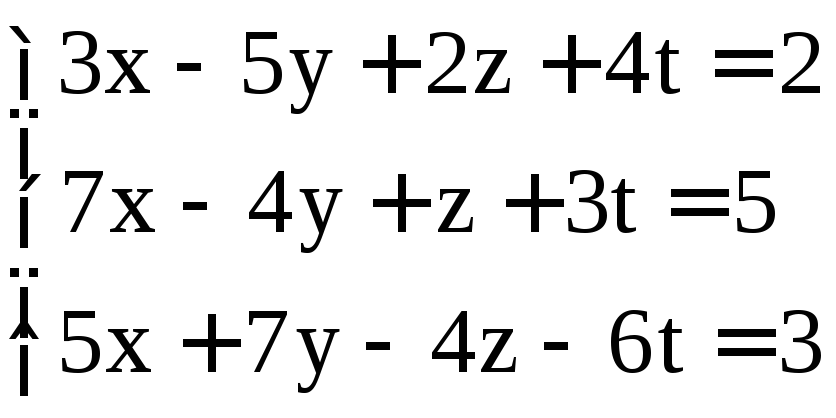 ;
;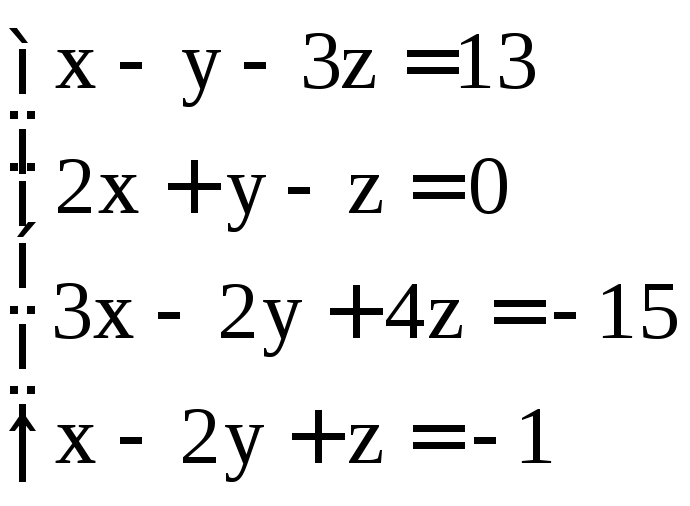 .
.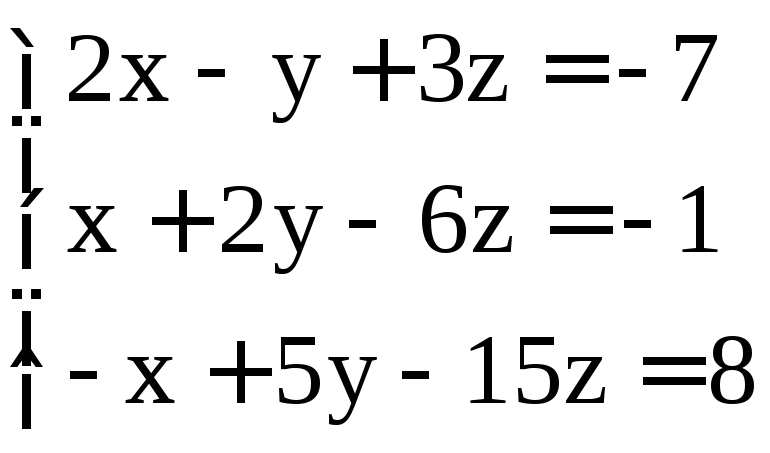 ;
;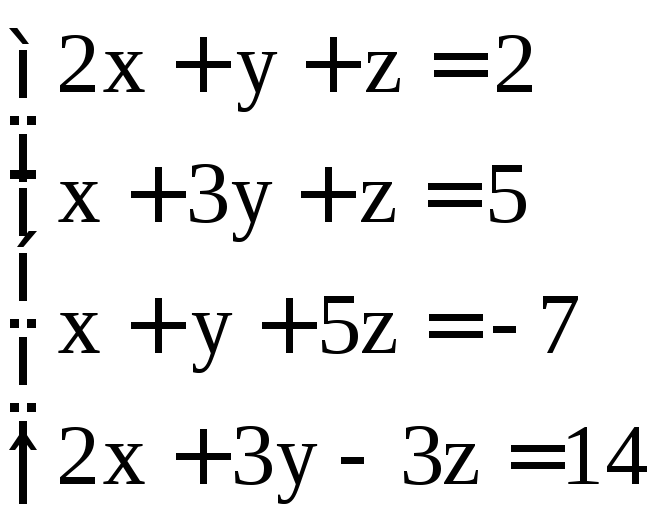 ;
;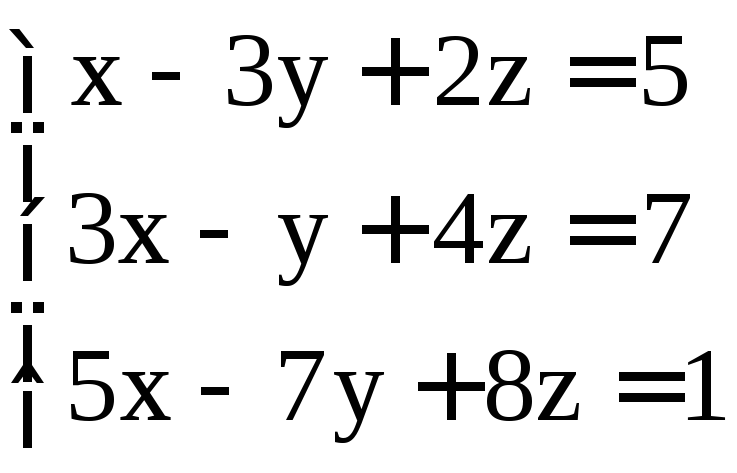 ;
; .
.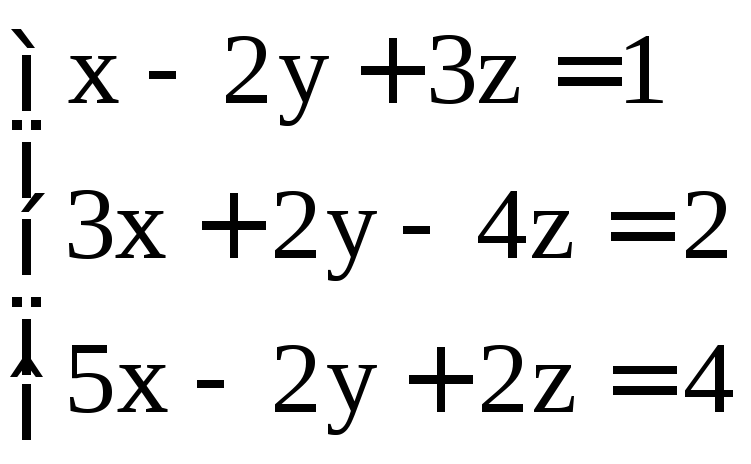 ;
;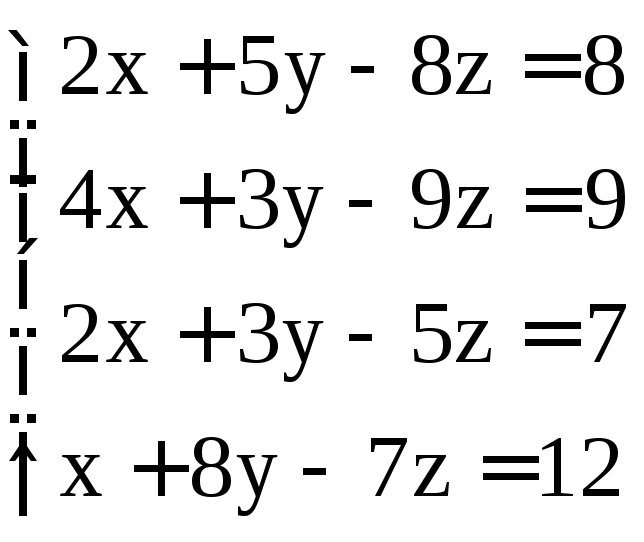 ;
;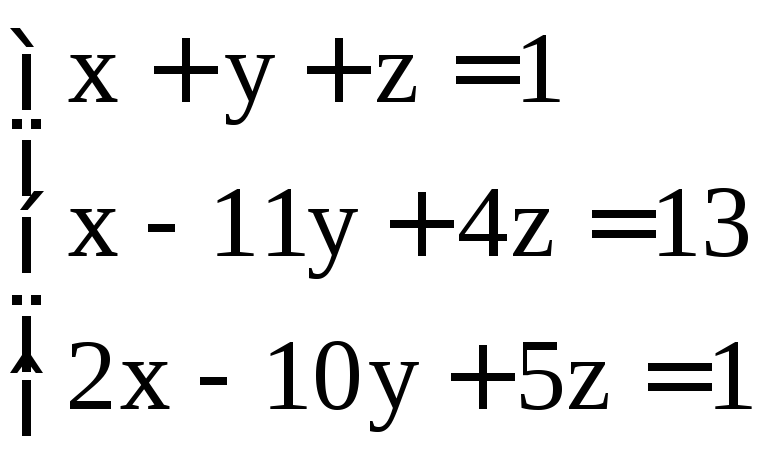 ;
;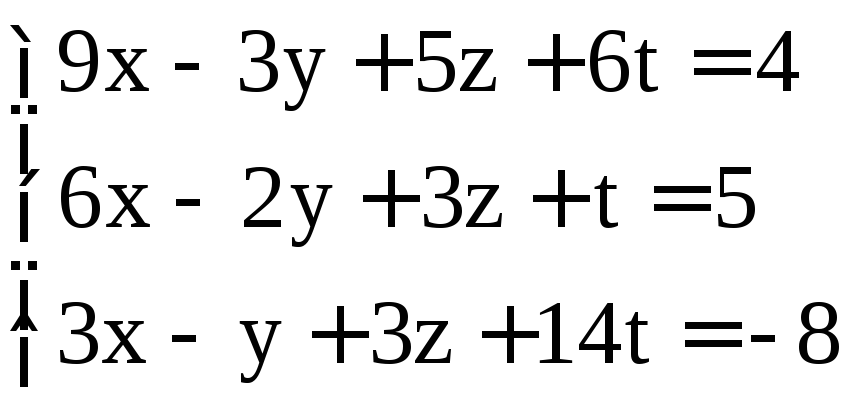 .
.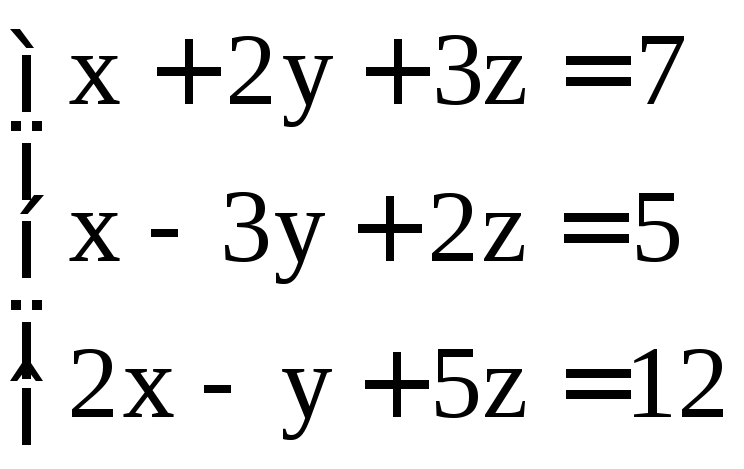 ;
;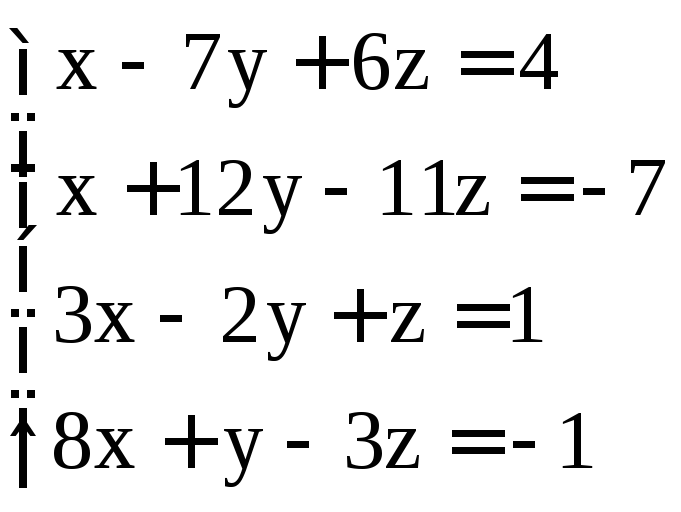 ;
;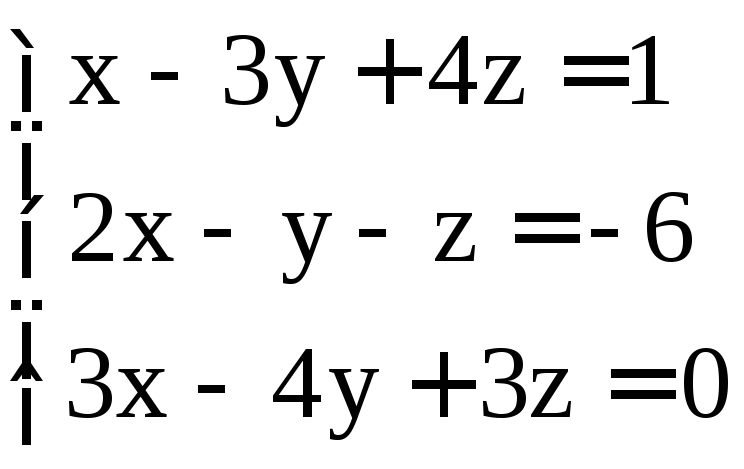 ;
; .
. ;
;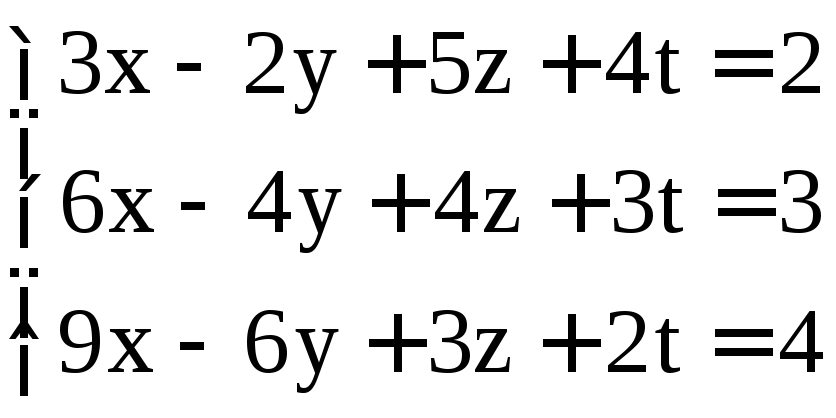 ;
;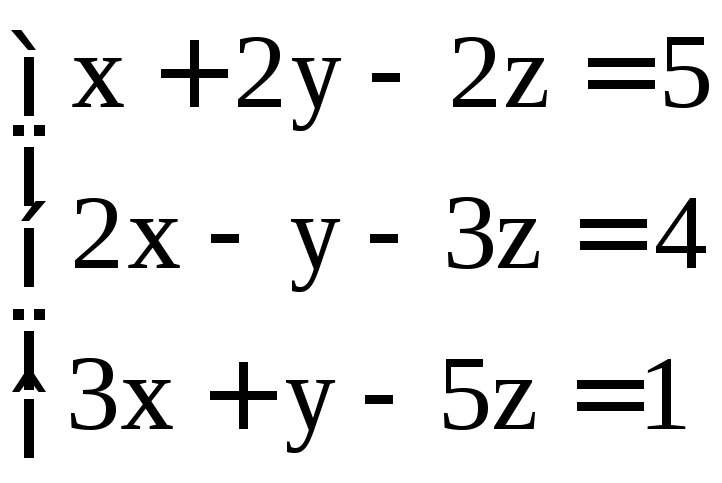 ;
;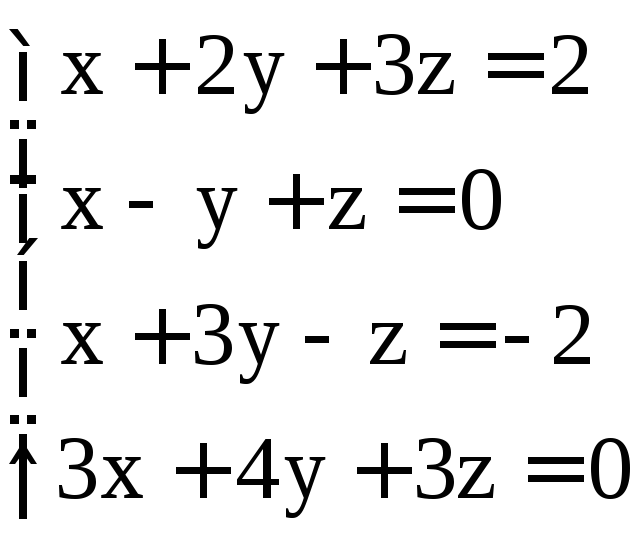 .
. ;
;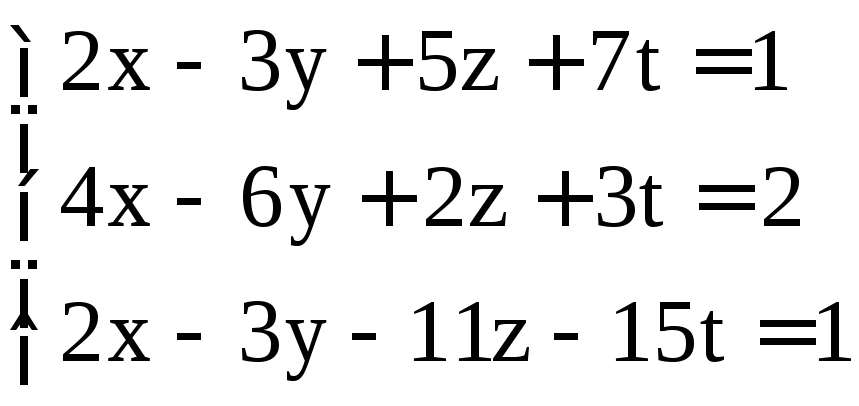 ;
;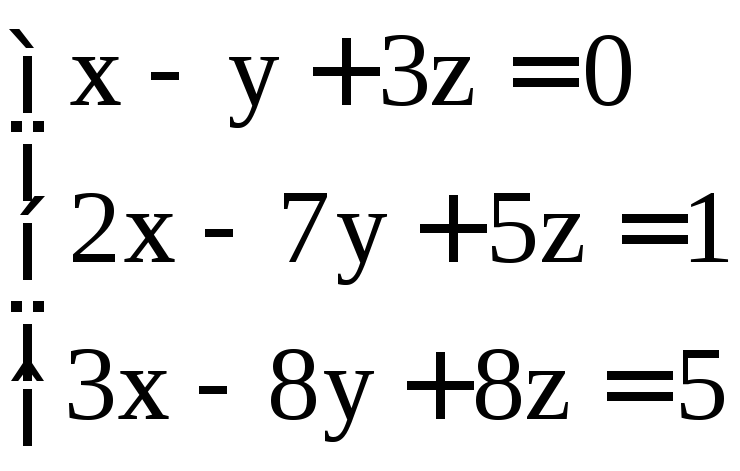 ;
;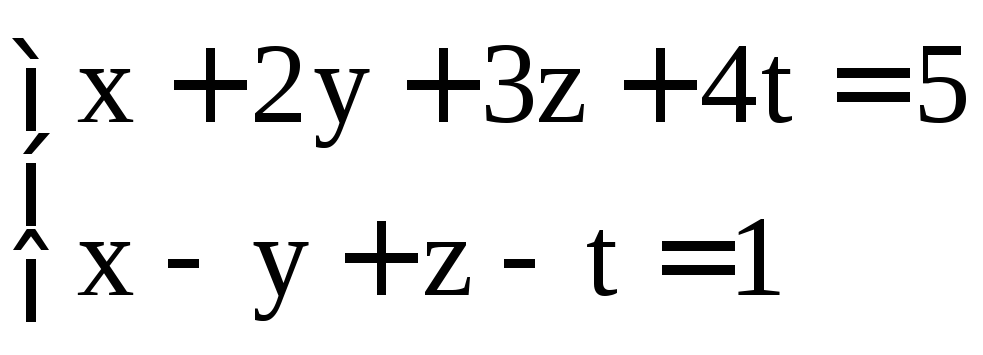 .
.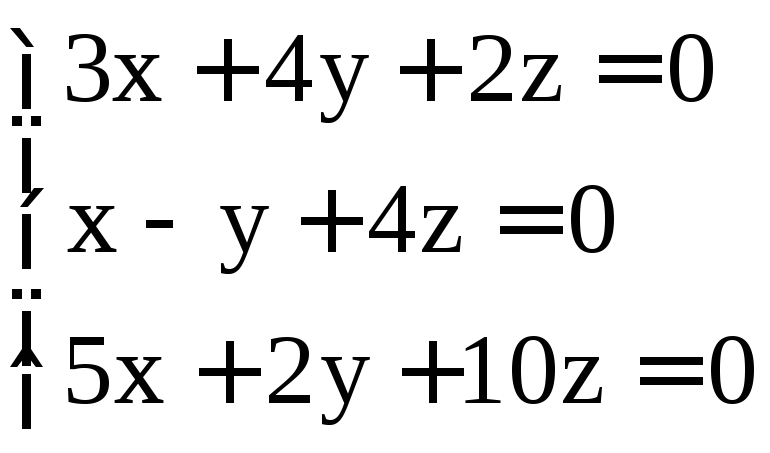 ;
;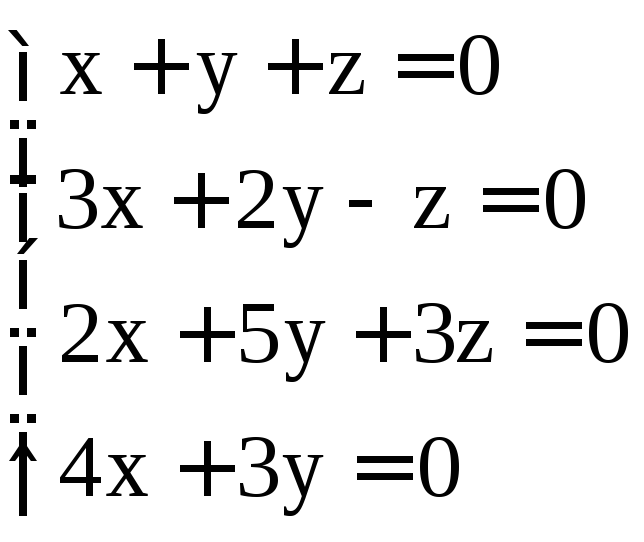 .
.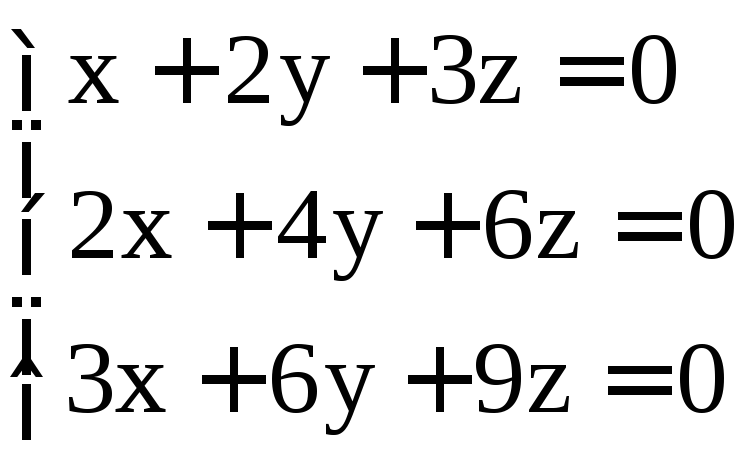 ;
;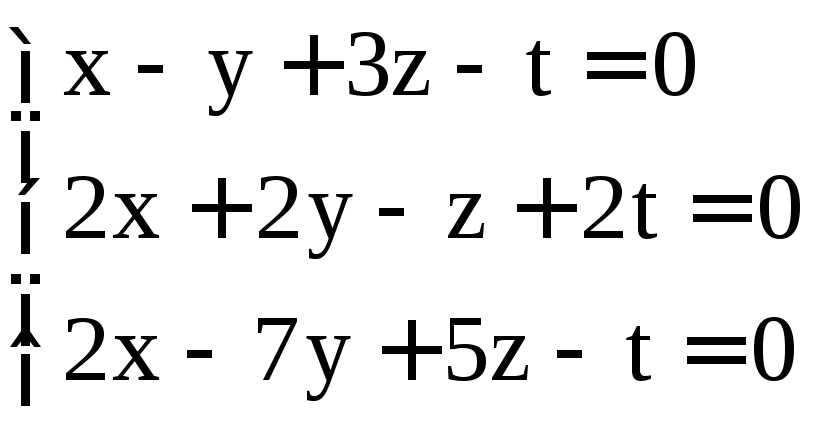 .
. ;
;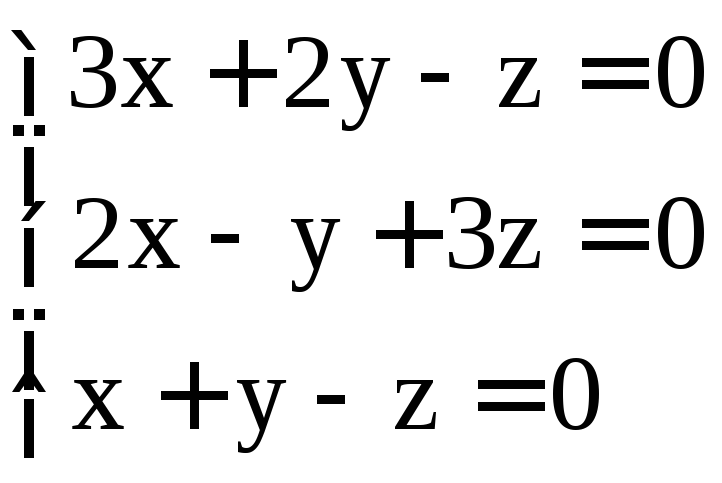 .
. ;
;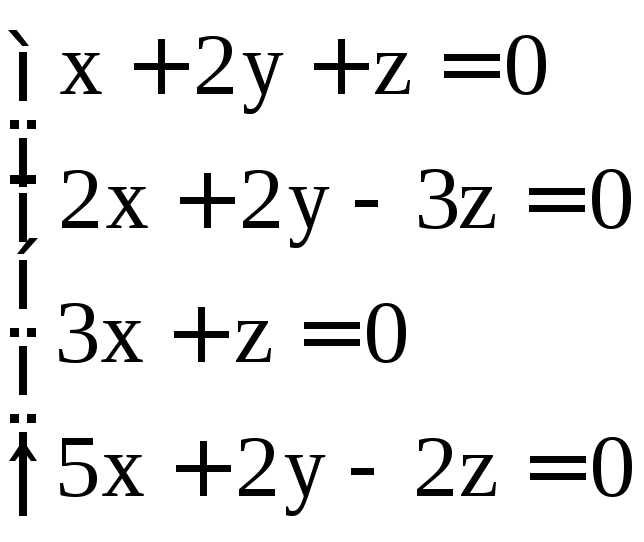 .
.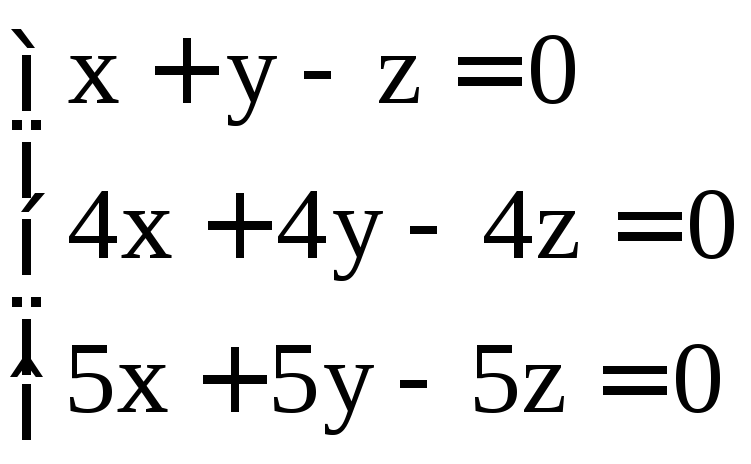 ;
;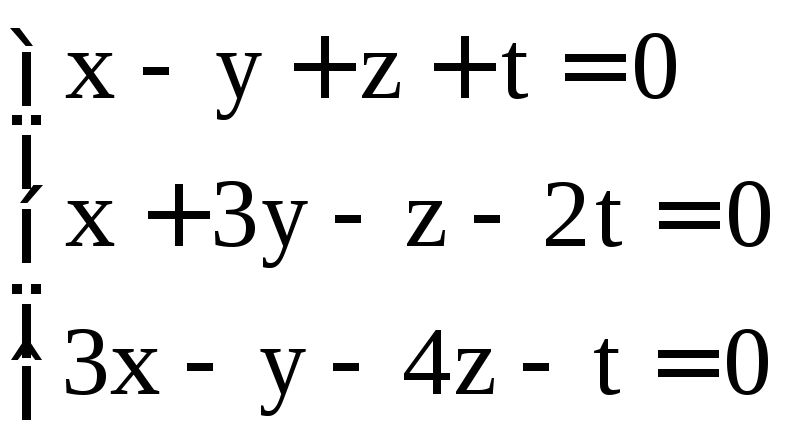 .
.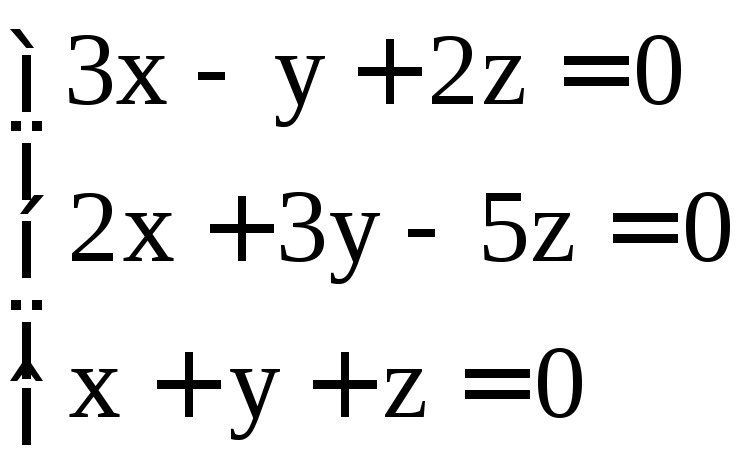 ;
;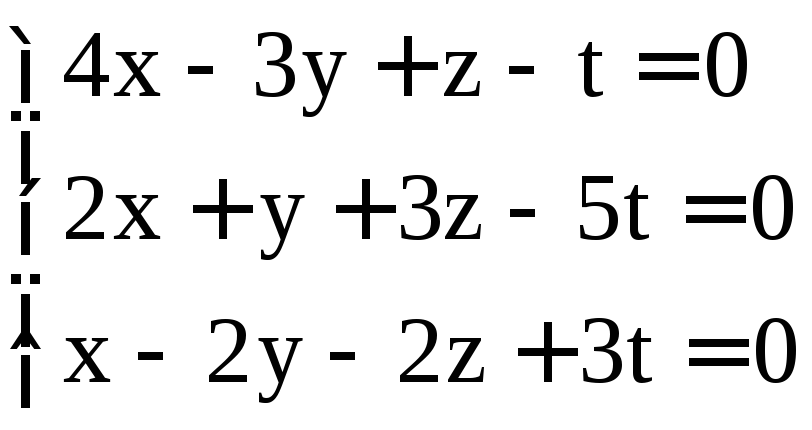 .
.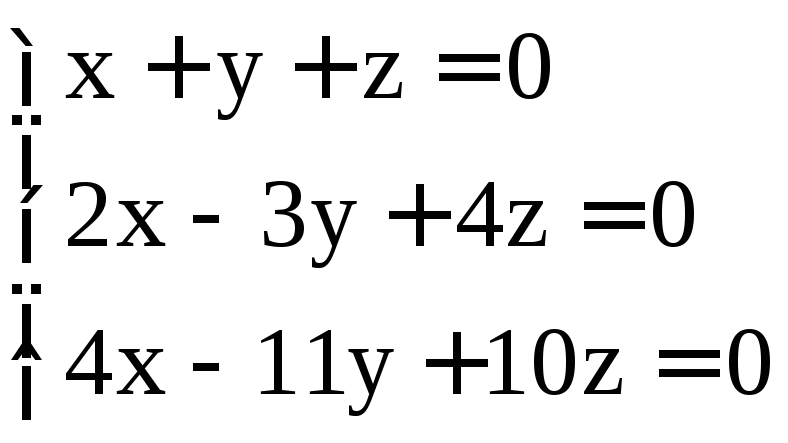 ;
;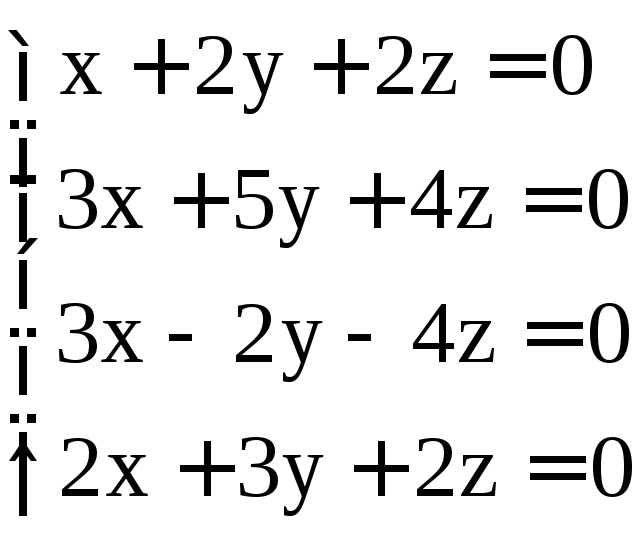 .
. ;
;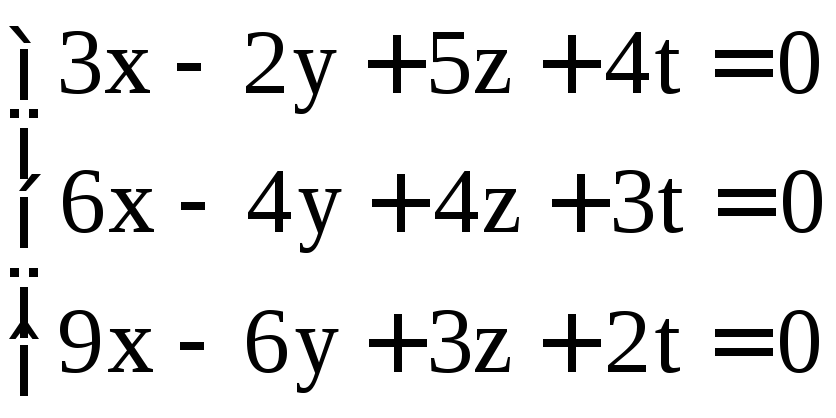 .
. ;
;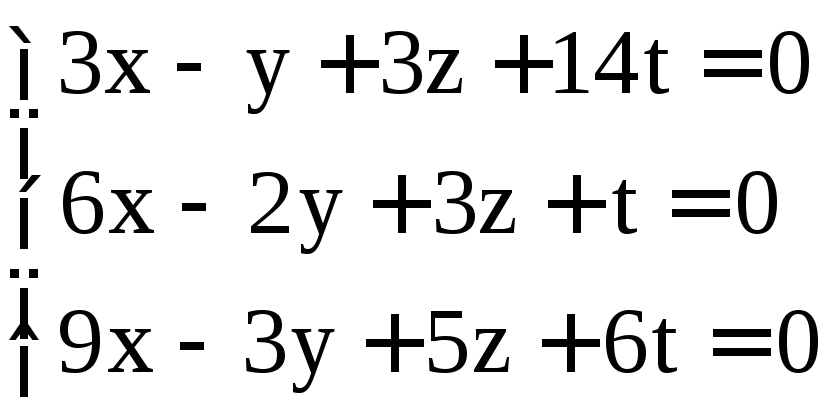 .
.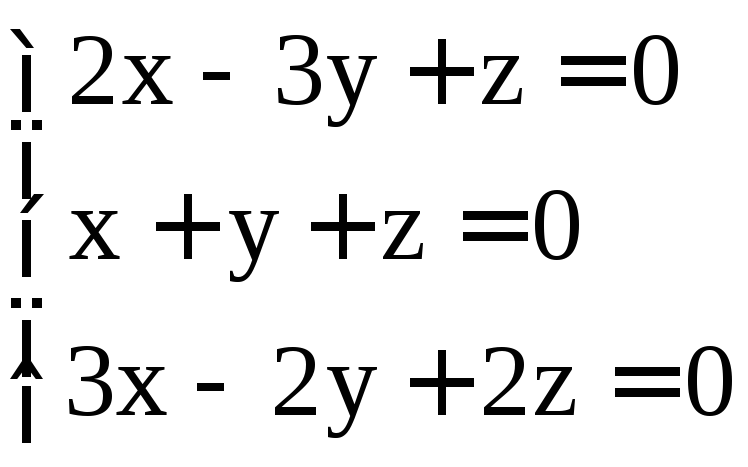 ;
;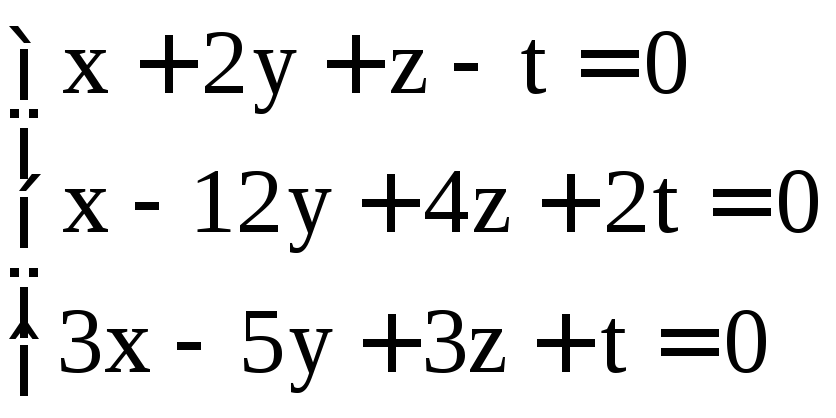 .
.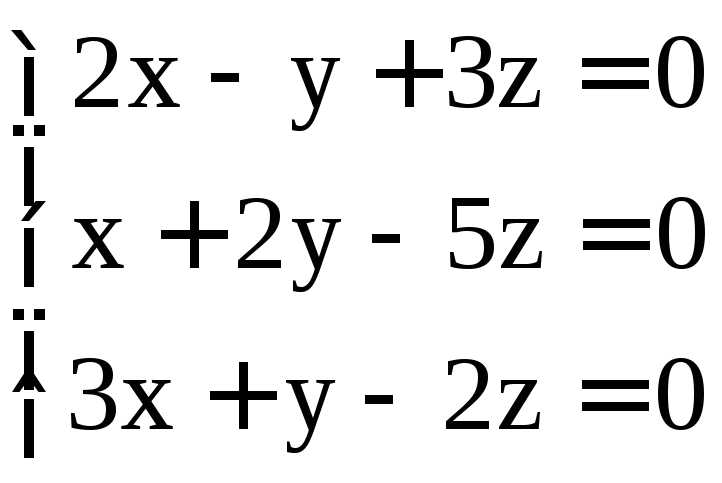 ;
;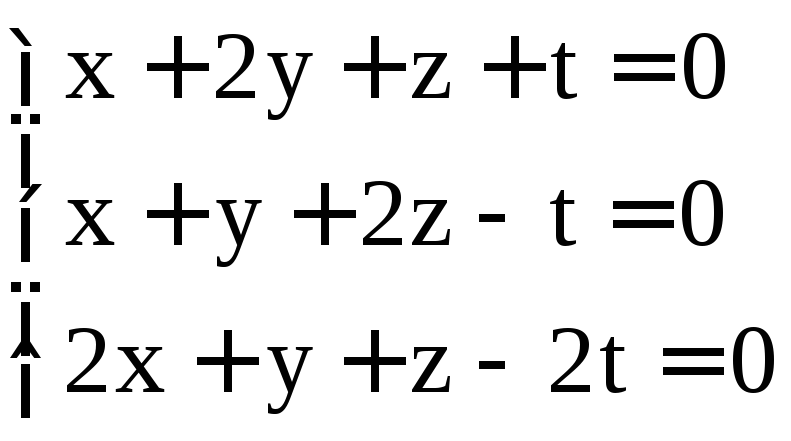 .
.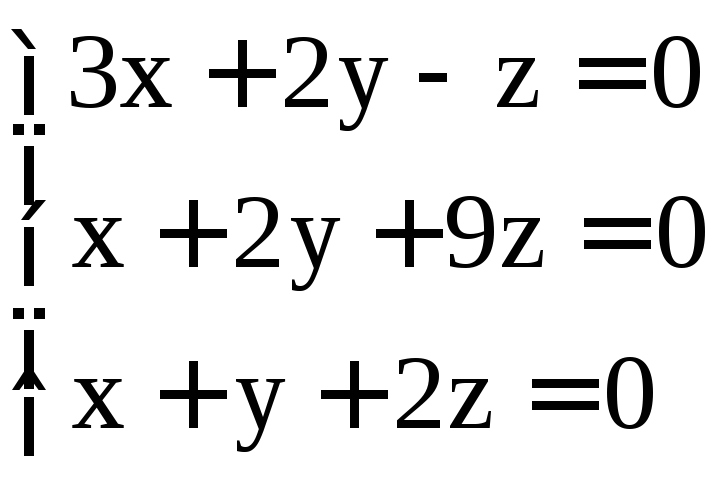 ;
;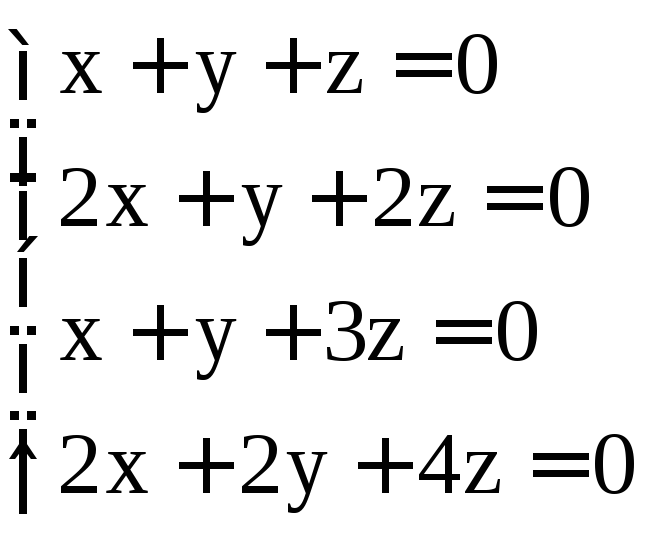 .
.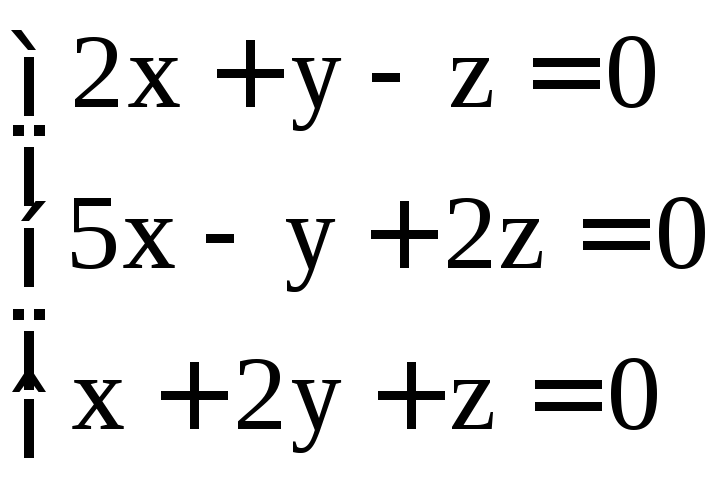 ;
;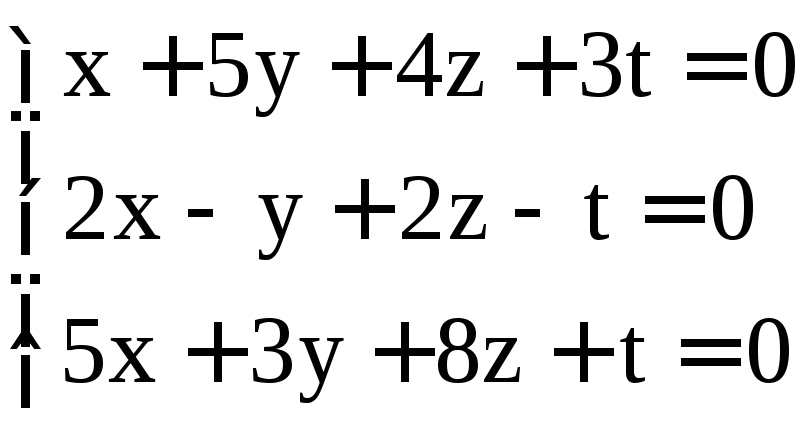 .
.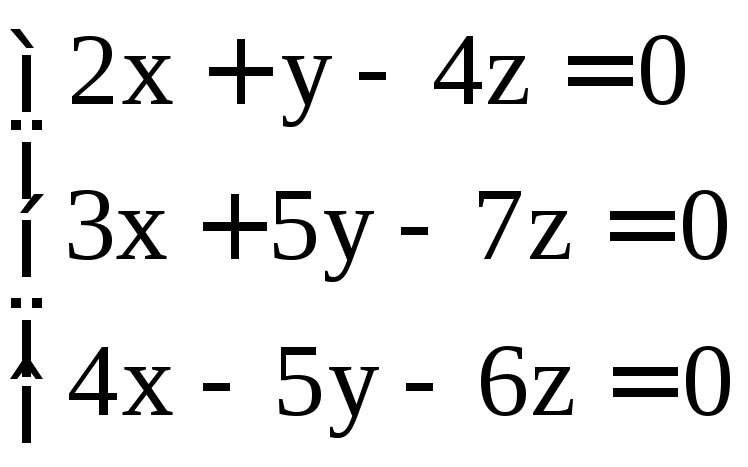 ;
;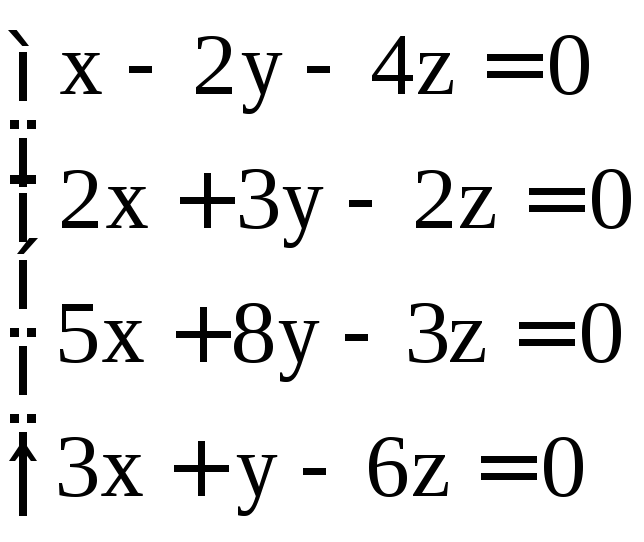 .
.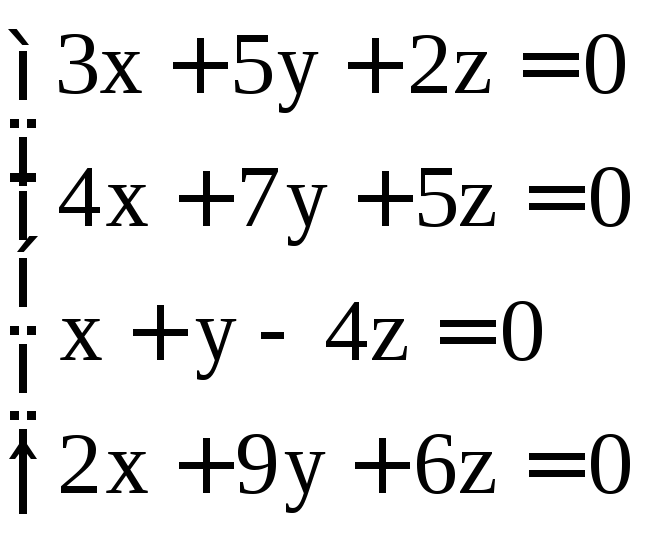 ;
;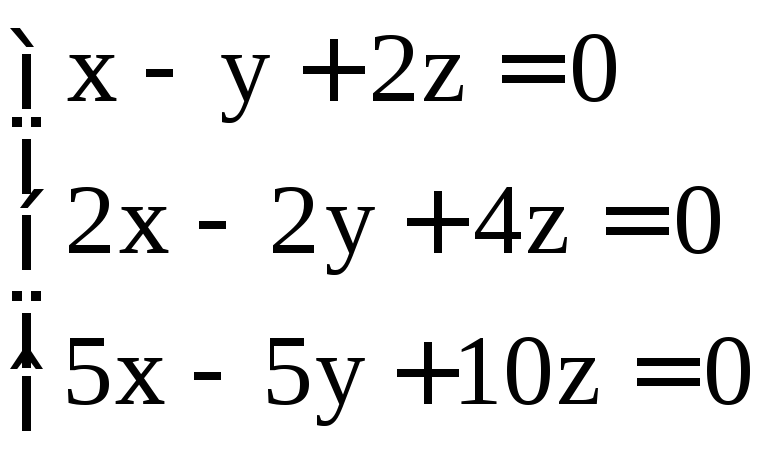 .
.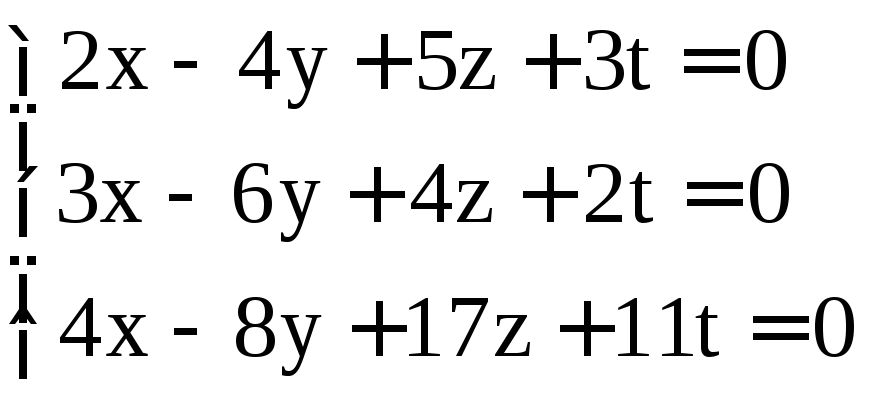 ;
; .
. ;
; .
. ;
;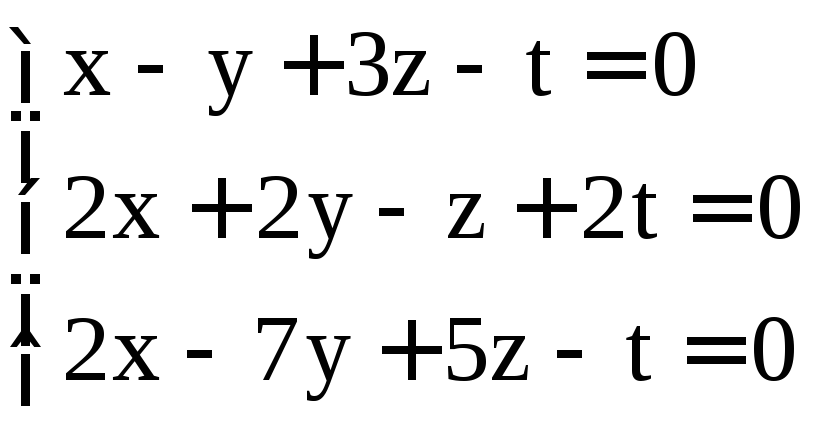 .
.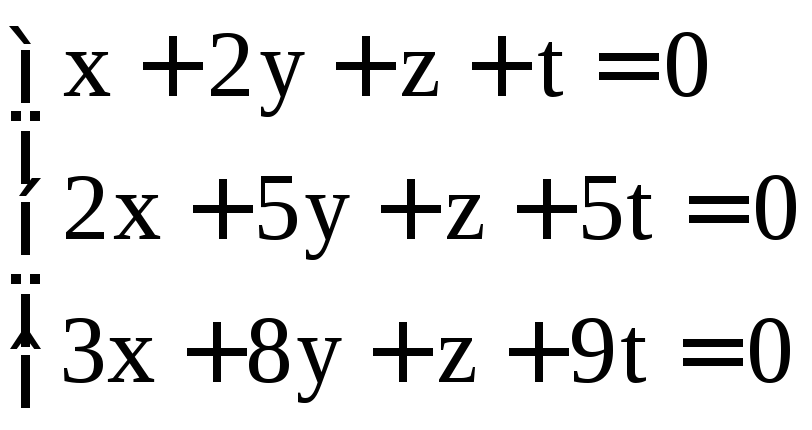 ;
;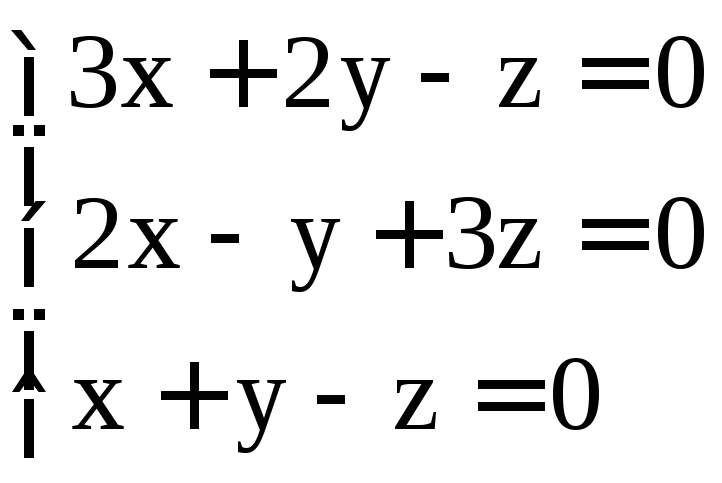 .
.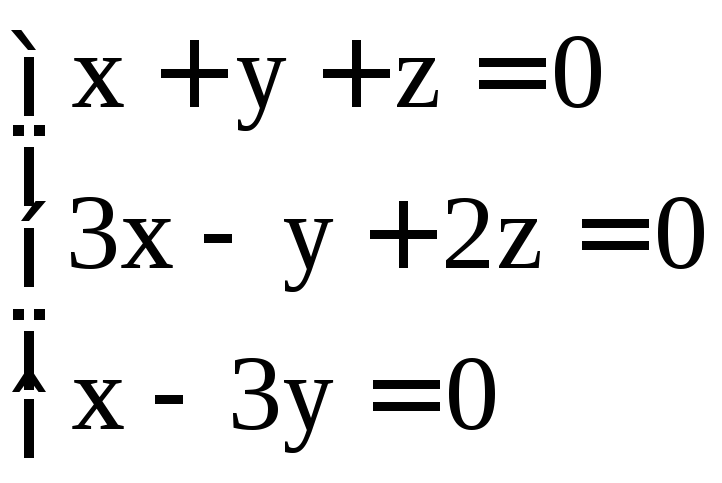 ;
;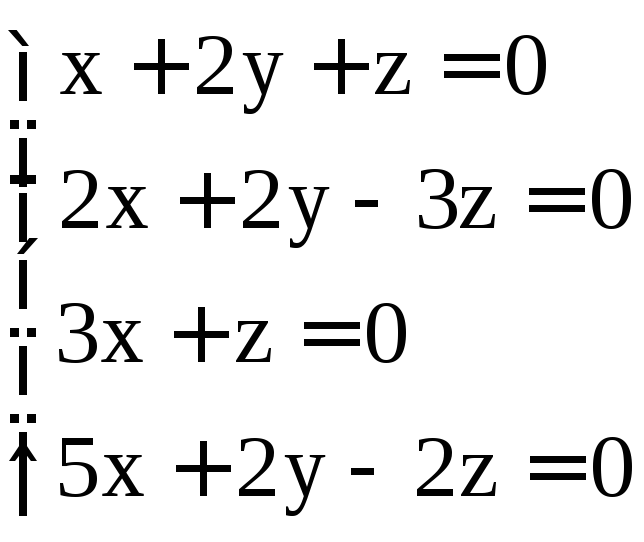 .
.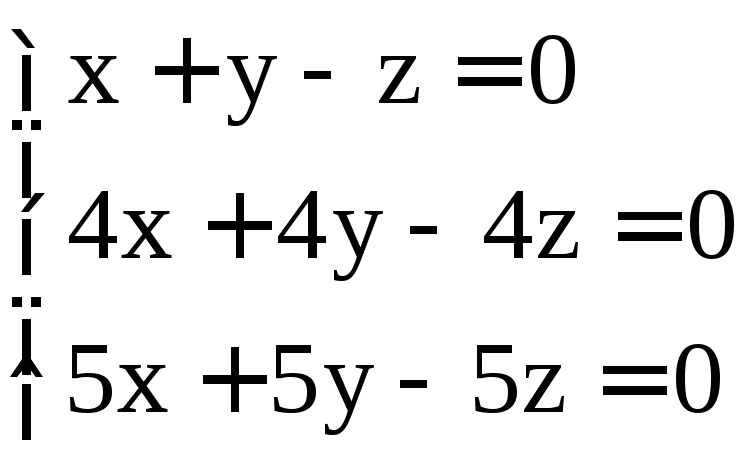 ;
;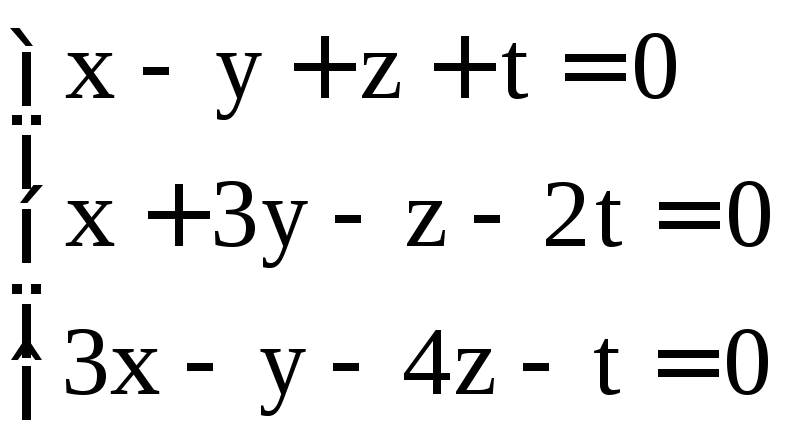 .
.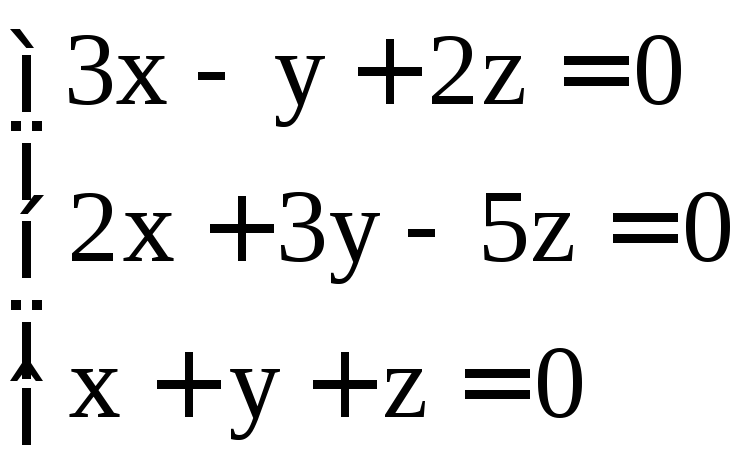 ;
;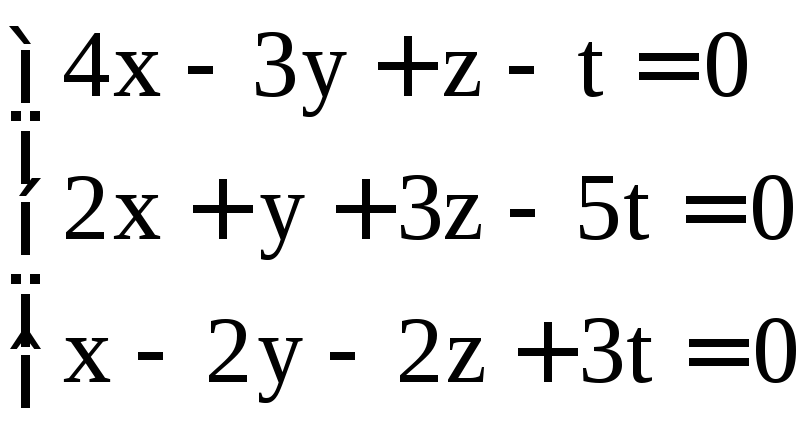 .
.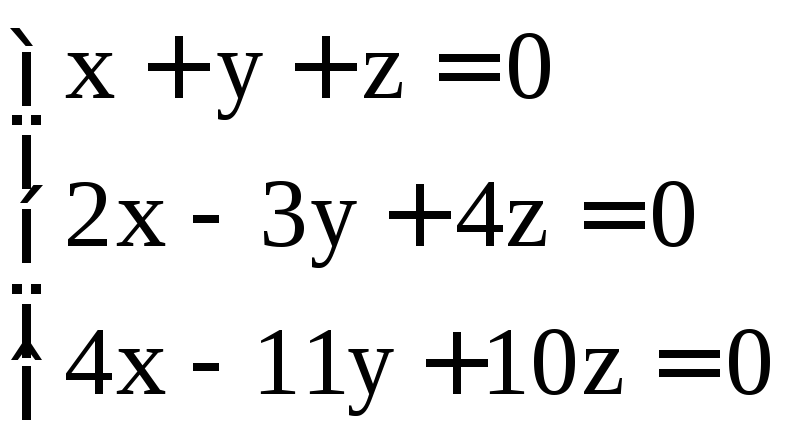 ;
;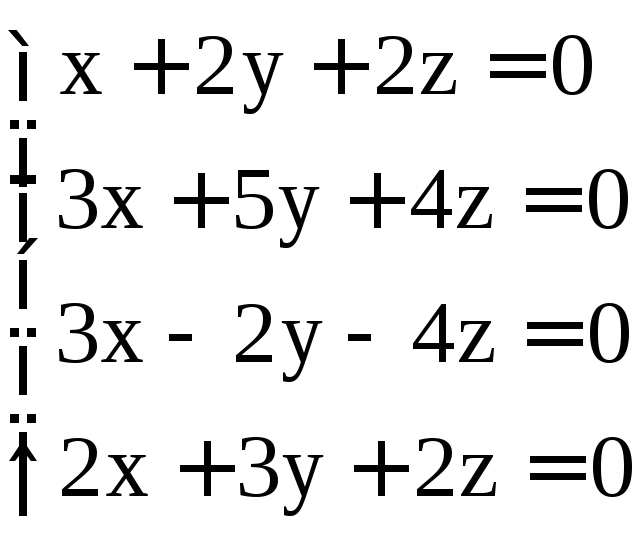 .
. ;
;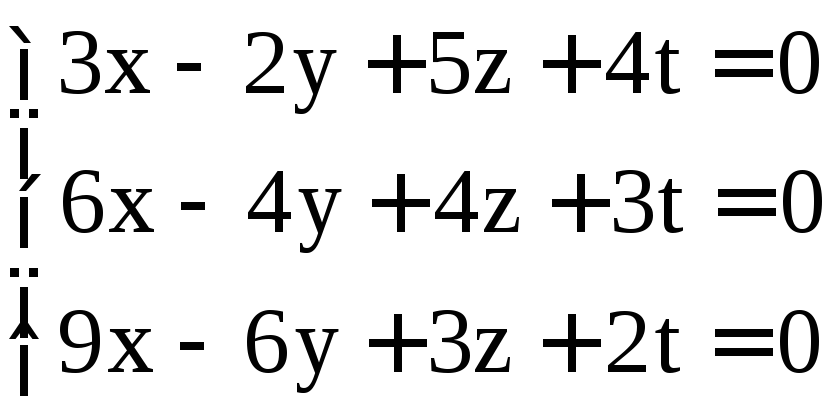 .
.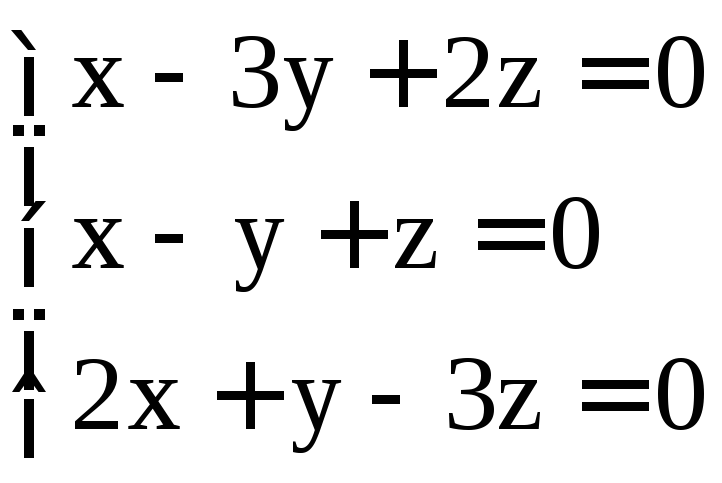 ;
;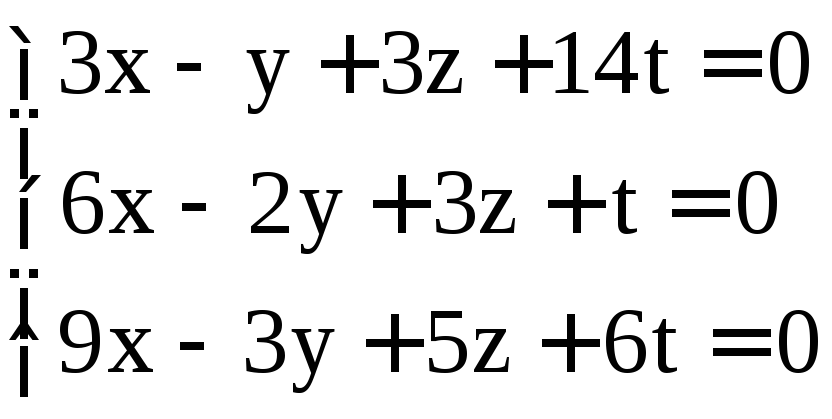 .
.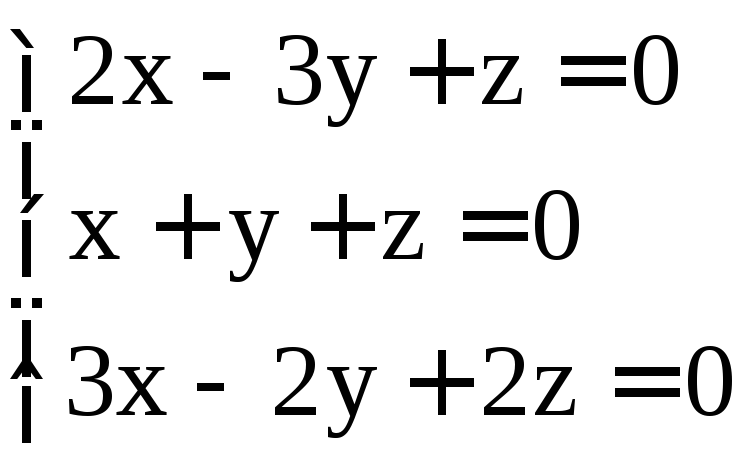 ;
;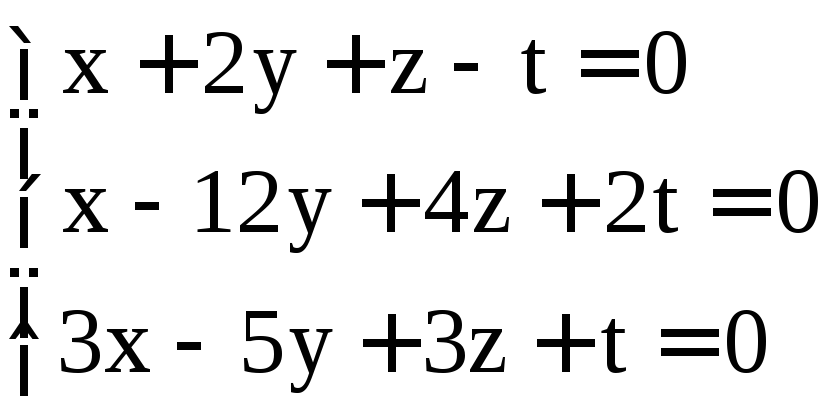 .
.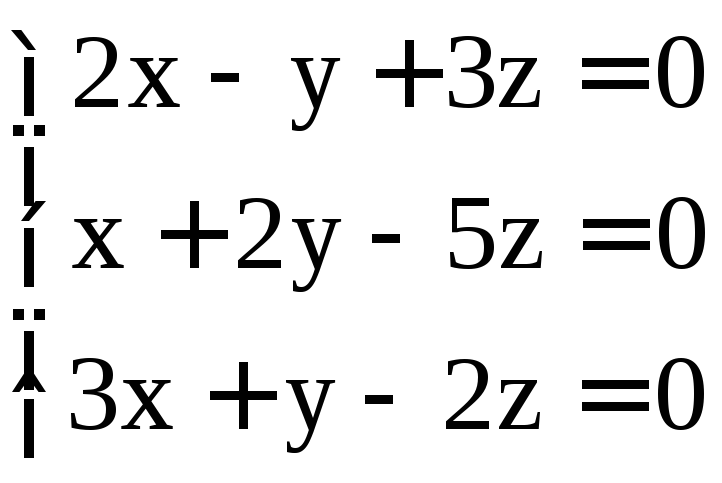 ;
;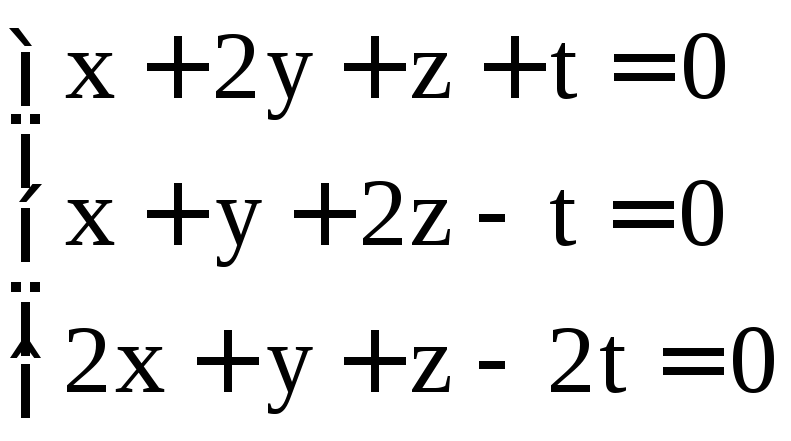 .
.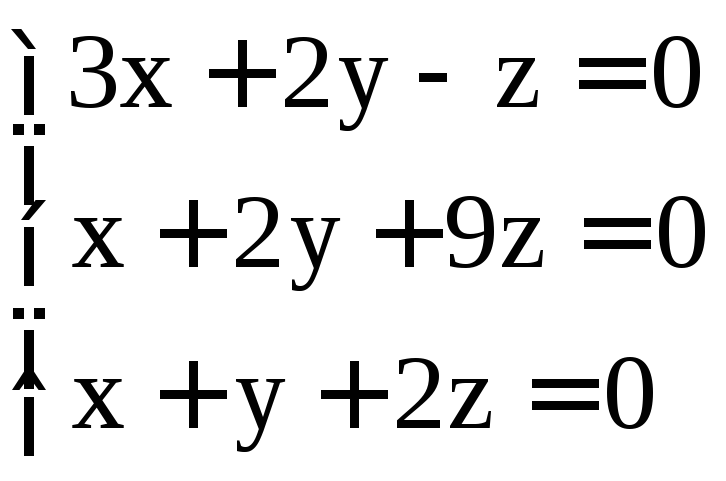 ;
;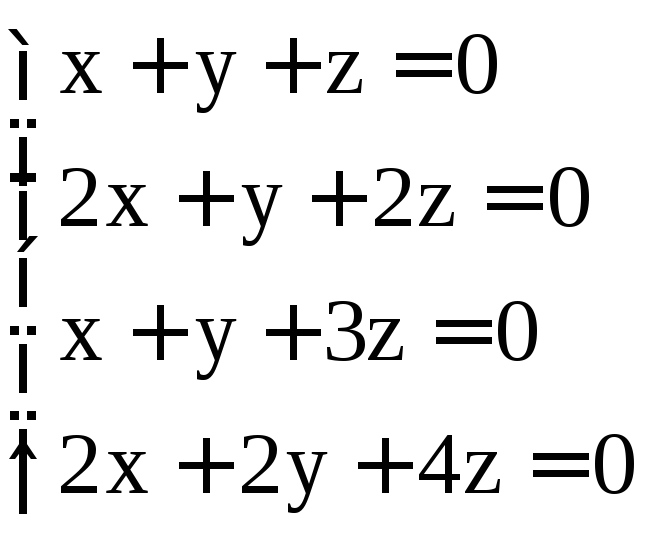 .
. ;
;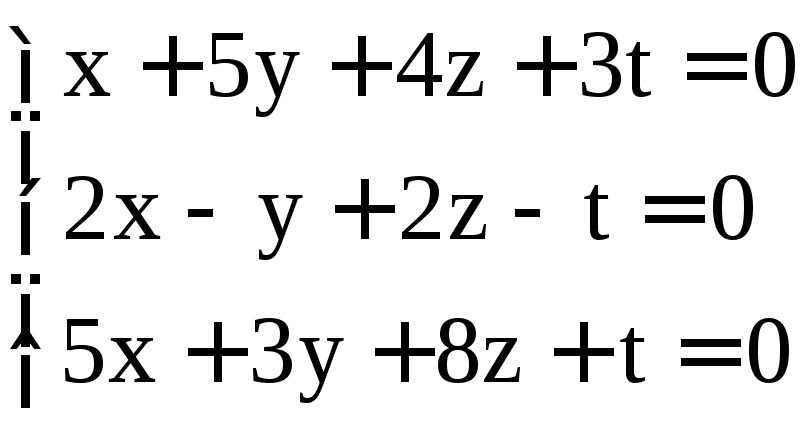 .
.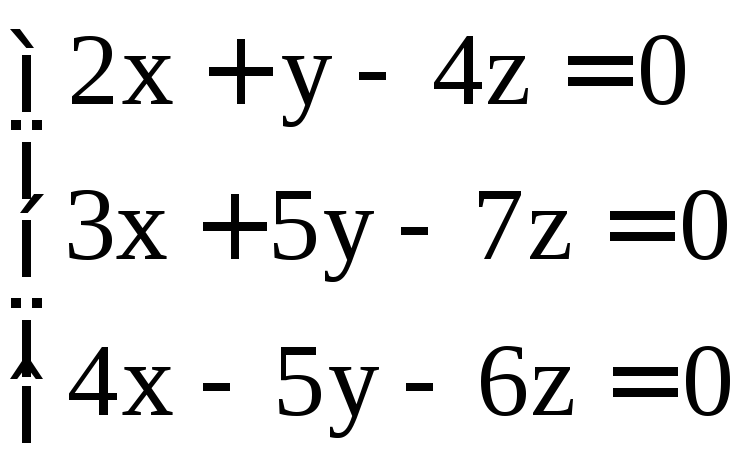 ;
;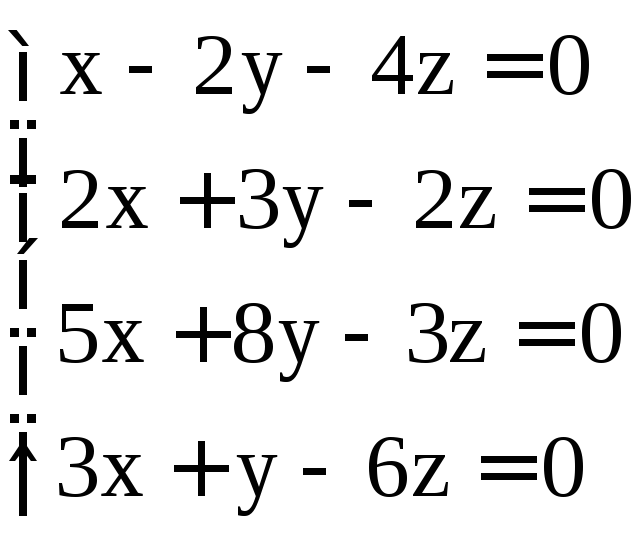 .
.