18.Уравнение Максвелла в комплексной форме.

Полная система уравнений Максвелла в комплексной форме.

 

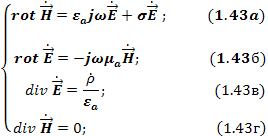
19.Волновое уравнение векторов н и е.

Волновое уравнение в математике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике).  

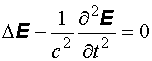.                                                                                                    (12.6)

 Аналогичным образом, исключая  из уравнений (12.1) и (12.2), находим, что вектор  удовлетворяет волновому уравнению:

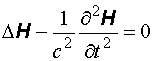 ,                                                                                                    (12.7)

 где 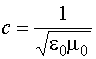 – скорость волны. Уравнения (12.6) и (12.7) – это волновые уравнения для векторов  и  соответственно. Из того, что векторы  и  удовлетворяют волновому уравнению, вытекает, что электромагнитное поле, которое характеризуют эти векторы, может распространяться в виде волны. Но волны возникают лишь тогда, когда их возбуждают.  Электромагнитные волны возбуждаются зарядами и токами. Но, возникнув, электромагнитная волна существует и тогда, когда породивших ее токов и зарядов уже нет. Этим переменное поле отличается от статического, которое не может существовать без порождающих его зарядов. Из уравнений (12.6) и (12.7) следует, что электромагнитные волны могут распространяться и в вакууме. 

20.Теорема и вектор Пойтинга в стационарном магнитном поле.

Вектор Пойнтинга

,

Теорема Пойнтинга в интегральной форме:

,

Теорема Пойнтинга — теорема, описывающая закон сохранения энергии электромагнитного поля.

Электромагнитные волны являются поперечными.

Вектора E и H колеблются в одинаковой фазе во взаимно перпендикулярных плоскостях.

Чтобы волна не затухала, из закона сохранения энергии следует:

Что плотности энергии электрического и магнитного полей в любой момент времени должны быть одинаковыми (равными).

, S = E*H – Вектор Пойнтинга

Непосредственно замеряемой в опытах величиной, характеризующей энергию, переносимую волной, является интенсивность.

Интенсивность – величина равная среднему значению модуля вектора Пойнтинга.

21.Теорема Пойтинга в комплексной форме.

22.Составляющая вектора магнитной напряженности н плоской электромагнитной волны . Длинна волны и фазная скорость .

Энергия, переносимая волной.

Для характеристики энергии, переносимой волной, применяется 2 величины:

Физическая величина равная энергии переносимой волной, через некоторую поверхность, называется ПОТОКОМ ЭНЕРГИИ.

Плотность потока энергии j – вектор, равный потоку энергии переносимой через единичную площадку, расположенную перпендикулярно направлению распространения волны.

– плотность энергии волны

- Вектор Умова.

Волны.

Волна – процесс распространения колебаний в пространстве. Они бывают механические и электромагнитные.

Механические волны распространяются в некоторой среде (газе, жидкость, твёрдом теле).

Электромагнитные волны распространяются в пустоте.

Волны бывают поперечные и продольные.

В поперечной волне колебания совершаются перпендикулярно направлению распространения волны.

В продольной волне колебания совершаются вдоль направления распространения волны.

Распространения волны не связано с переносом вещества. Однако волна переносит энергию.

Длина волны – расстояние на которое распространяется волна за один период колебаний.

; ; ;

Волновая поверхность – геометрическое место точек (ГМТ), колеблющихся в одинаковой среде.

Фронт волны – передняя волновая поверхность, то есть ГМТ до которых дошли колебания в данный момент времени (фронт волны движется).

В зависимости от формы фронта волны различают на плоские, цилиндрические и сферические волны.

Уравнение плоской волны, распространяющейся вдоль оси Х.(обобщенная координата).

– фазовая скорость

Мы получили, что со скоростью 𝜐 движется фронт волны, то есть передняя поверхность постоянной фазы.

Поэтому данную скорость называют фазовой скоростью.

Так как с фазовой скоростью, не движется ни какой материальный объект, то для неё нет ограничений, она может быть и больше скорости света.

За перенос энергии волны отвечает другая скорость – групповая.

Уравнение плоской волны распространяющейся в произвольном направлении.

, где r – это радиус-вектор точки

k=m*n

– координатное представление

Уравнение сферической волны.

, где r – это радиус сферы.