11.Проводники в электростатическом поле
Электростатическое поле - эл.поле, образованное неподвижными электрическими зарядами. Свободные электроны - электроны, способные свободно перемещаться внутри проводника ( в основном в металлах) под действием эл. поля; Свободные электроны возникают при образовании металлов: электроны с внешних оболочек атомов утрачивают связи с ядрами и начинают принадлежать всему проводнику;
-
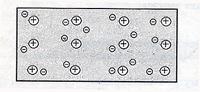участвуют в тепловом движении и могут
свободно перемещаться по всему
проводнику.
Электростатическое
поле внутри проводника
-
внутри проводника электростатического
поля нет ( Е = 0 ), что справедливо для
заряженного проводника и для незаряженного
проводника, внесенного во внешнее
электростатическое поле.
Почему? -
т.к. существует явление
электростатической индукции, т.е.
явление
разделения зарядов в проводнике,
внесенном в электростатическое поле (
Евнешнее) с образованием нового
электростатического поля ( Евнутр.)
внутри проводника.
Внутри
проводника оба поля ( Евнешн. и Евнутр.)
компенсируют друг друга, тогда внутри
проводника
Е = 0.
Заряды можно разделить:
Электростатическая
защита
-
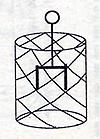металл. экран, внутри которого Е = 0, т.к.
весь заряд будет сосредоточен на
поверхности проводника.
Электрический
заряд проводников
-
весь статический заряд проводника
расположен на
его поверхности, внутри
проводника q = 0;
- справедливо для
заряженных и незаряженных проводников
в эл.поле.
Линии напряженности эл.поля
в любой точке поверхности
проводника перпендикулярны этой
поверхности.
12.Закон Ома в дифференциальной форме.
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
|
|
|
(7.6.1) |
|
Для однородного линейного проводника выразим R через ρ:
|
|
|
| ||
|
|
(7.6.3) |
| ||
,
,это запись закона Ома в дифференциальной форме.
Здесь 
– удельная
электропроводность.
Размерность
σ – [
].
|
13.Граничные условия на поверхности раздела двух проводящих тел |
|
Под граничными условиями понимают условия, которым подчиняется поле на границах раздела сред с различными электрическими свойствами. При интегрировании уравнения Лапласа (или Пуассона) в решение входят постоянные интегрирования. Их определяют из граничных условий. В проводящем теле, находящемся в магнитном поле, вследствие явления электростатической индукции происходит разделение зарядов (рис. 15.5).
Рис. 15.5. разделение зарядов в проводящем теле Все точки тела будут иметь один и тот же потенциал (иначе появилось бы упорядоченное движение зарядов). Поверхность тела эквипотенциальна. Вектор напряженности внешнего поля в любой точке поверхности подходит к ней под прямым углом. Внутри проводящего тела напряженность равна нулю, так как внешнее поле компенсируется полем зарядов, расположившихся на поверхности тела. На границе раздела проводящего тела и диэлектрика при отсутствии тока по проводящему телу выполняются два условия: 1. Отсутствует тангенциальная (касательная к поверхности) составляющая напряженности поля
2.
Вектор электрического смещения
На границе раздела двух диэлектриков с различными диэлектрическими проницаемостями выполняются следующие условия: 1. Тангенциальные составляющие напряженности поля равны: Et1 = Et2. (15.23) 2. Нормальные составляющие электрической индукции равны: Dn1 = Dn2. (15.24) Уравнения Лапласа и Пуассона являются уравнениями в частных производных, которые в общем случае имеют множество линейно независимых друг от друга решений. Выбор единственного решения, удовлетворяющего конкретной задаче, производят с помощью граничных условий.
|
(15.21)
в
любой точке диэлектрика, непосредственно
примыкающей к поверхности проводящего
тела, численно равен плотности заряда
σ на поверхности проводящего тела в
этой точке:
(15.22)