3.Градиент скалярной величины . Вихревое поле.
Градие́нт — вектор,
своим направлением указывающий
направление наибольшего возрастания
некоторой величины 
,
значение которой меняется от одной
точки пространства к другой (скалярного
поля),
а по величине (модулю) равный быстроте
роста этой величины в этом направлении.
Градиент скалярной величины – векторная величина, численно равная производной от этой функции по направлению нормалей к поверхности уровня.
Смысл
градиента любой скалярной функции 
в
том, что его скалярное произведение с
бесконечно малым вектором
перемещения 
дает полный
дифференциал этой
функции при соответствующем изменении
координат в пространстве, на котором
определена 
,
то есть линейную (в случае общего
положения она же главная) часть
изменения 
при
смещении на 
.
Применяя одну и ту же букву для обозначения
функции от вектора и соответствующей
функции от его координат, можно написать:
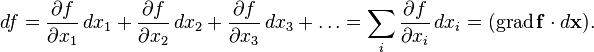
Градиент численно равен максимальной скорости изменения функции. Направление градиента совпадает с направлением быстрейшего изменения функции.
Вихревые поля - поля с замкнутыми силовыми линиями. Создается магнитным полем и индукционным электрическим полем (при изменении магнитного потока).
Индукционное электрическое поле является вихревым. Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока
4.Дивергенция вектора. Принцип непрерывности линий магнитной индукции.
Дивергенция – скалярная характеристика векторного поля.
Дивергенция векторного поля скалярная величина, равная пределу отношения потока через замкнутую поверхность к объёму, заключенному внутри этой поверхности, при условии, что эта плоскость стягивается к точке.
Она характеризует интенсивность источников поля ( если div F = 0, то источники поля отсутствуют)
Поток
вектора магнитной индукции 
сквозь
любую замкнутую поверхность 
равен
нулю:
,
где для однородных изотропных сред
;
–напряженность
магнитного поля; 
–
абсолютная магнитная проницаемость
среды; 
–
относительная магнитная проницаемость
среды; 
–
магнитная постоянная.
Геометрический смысл закона: линии вектора магнитной индукции всюду непрерывны и замкнуты.
Этот
принцип определяет, что линии магнитной
индукции непрерывны (магнитное поле не
имеет ни стоков, ни истоков). Линии
магнитной индукции – линии проведенные
(построенные) в магнитном поле так, что
в каждой их точке касательные совпадают
по направлению с вектором 
.
Рассмотрим один из простых и наглядных примеров. На рис.1.5 представлен прямолинейный провод круглого сечения, ток i в котором направлен от наблюдателя. Линии магнитной индукции – концентрические окружности с центром на оси провода. Направление линий связано с направлением тока правилом правого винта.
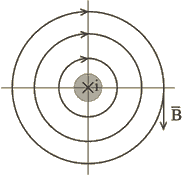Рис.1.5
Источниками магнитных полей являются электрические токи.
Принцип непрерывности магнитного потока математически записывается так:
-
(1.6.)
магнитный поток сквозь любую замкнутую поверхность равен нулю.