Ответы на все вопросы по линейной алгебре

1.Матрица – прямоугольная таблица размером m*n

2. размер матрицы: прямоугольная таблица из m и n чисел содержащая m строк и n столбцов

3. элемент матрицы a_ij находится в 3 строке 4 столбце

4. матрица называется квадратной, если число строк = числу столбцов (m=n)

5. число n (если матрица квадратная) называется порядком матрицы

6. две квадратные матрицы( 4 и 5 порядков) не могут быть равны

7. диагональные - элементы квадратной матрицы у которых номер строки равен номеру столбца (образуют главную диагональ)

8. диагональная матрица – у которой все недиагональные элементы =0

9. равными называются матрицы одинаковой размерности

10. нулевая матрица – если все элементы её равны 0

11. единичная матрица - диагональная матрица у которой все элементы главной диагонали равны 1

12. элементы равные единицы

13.единичная матрица может быть прямоугольной

14. транспонирование матрицы - замена каждой её строки столбцом с тем же номером

15.от транспонирования размер не меняется

16.матица столбец

17.матрица строка

18. суммой двух матриц (А и В) одинаковой размерности называется матрица С той же размерности каждый элемент С_ij которой равен сумме элементов А_ij+B_ij стоящих на одинаковых местах в слагаемых матрицах А и В. Матрицы складываются поэлементно.

19.матрицы одинаковой размерности

20.нет,нельзя

21. произведением матрицы А на число называется матрица λА с элементами (λ_ij) той же размерности что и исходная каждый элемент которой равен произведению соответствующего элемента исходной матрицы на число λ

22. свойства операции сложения матриц: А+В=В+А , (А+В)+С=А+(В+С) ,если О нулевая матрица то А+О=О+А=А, (А+В)^Т=А^Т+В^Т

23. свойства операции умножения матрицы на число: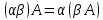,,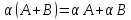 (, (^Т=α*А^Т

24. свойства операции умножения матриц: (АВ)С=А(ВС), α(АВ)=(αА)В=А(αВ), (А+В)С=АС+ВС, (АВ)^Т=В^ТА^Т

25.перестановочными матрицами называются 2 матрицы если АВ=ВА

26. произведение матрицы А на Е(единичная матрица)= А

27. операция умножения матриц коммутативна АВВА если существует АВ то ВА может не существовать

28. умножение матриц размером 3*7 и 7*5 возможно

29. умножение матриц размером 4*6 и 4*8 невозможно

30. размер матрицы при умножении матриц размерами 12*9 и 9*5 = 12*5

31.да отличаются

32.признаки равенства определителя нулю: определитель содержащий 2 одинаковые строки или 2 пропорциональные строки =0, если одна из строк определителя целиком состоит из нулей или является линейной комбинацией его других строк, то определитель=0

33. тоже самое

34. определитель не меняется при транспонировании, если к элементам одной его строки прибавить соответствующие элементы другой его строки умноженное на одно и то же число.

35. минором М_ij элемента а_ij определителя квадратной матрицы А=( а_ij) n-ного порядка называется определитель (n-1)-ого порядка, полученный из матрицы А вычёркиванием i-строки и j-столбца на пересечении которых находится данный элемент

36. чтобы получить из матрицы А минор М₃₇ нужно вычеркнуть 3 строку и 7 столбец

37. алгебраическим дополнением А_ij элемента а_ij называется его минор М_ij, взятый со знаком (-1)^i+j* М_ij

38. минор М₈₅ и алгебраическое дополнение А₈₅ отличаются тем, что у минора будет знак (-), а у алгебр. дополнения (+)

39.минор М₂₆ и алгебраическое дополнение А₂₆ ничем не отличаются

40. теорема о разложении определителя: определитель n-ного порядка равен сумме произведений элементов любой его строки(столбца) на их алгебраические дополнения

41. сумма произведений элементов любой строки(столбца) определителя на их алгебраические дополнения равна определителю

42. сумма произведений элементов любой строки(столбца) определителя на их алгебраические дополнения соответствующих эементов другой строки равна нулю

43. матрица вырожденная если её определитель равен нулю

44. матрица невырожденная если её определитель отличен от нуля

45. обратной для квадратной матрицы А называется такая матрица А^-1, что АА^-1=А^-1А=

46.  Определитель произведения двух матриц равен произведению их определителей т.е.|AB|=|A||B| 

47. Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей

48. Для того, чтобы матрица А имела обратную, необходимо, чтобы ее определитель был отличен от нуля(была невырожденной)

49.для нахождения обратной матрицы необходимо: найти определитель исходной матрицы А, если 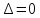, то обратной матрицы нет; находим алгебраические дополнения А_ij всех элементов матрицы А и построить из них новую А'; транспонировать матрицу А' и получить А*;разделить все элементы А* на определитель матрицы А

50.вид обратной матрицы:А^-1=

51.чтобы матрица имела себе обратную необходимо, чтоб определитель не равнялся 0

52.прямоугольная матрица не имеет себе обратную матрицу

53. вырожденная матрица не имеет себе обратную матрицу

54.данная матрица может иметь только 1 обратную матрицу

55.ступенчатая матрица – матрица вида 0 а_1к1…. а_1n , 0 0 а_2к2…. А_2n , ….., 0000 а_mкm…. А_mn

56.ступенчатая матрица не может содержать нулевые строки

57.высота каждой ступеньки ступенчатой матрицы одна строка

58.шириной ступеньки называется число элементов строки стоящих на ступеньке

59.нулевая матрица не может быть ступенчатой

60. единичная матрица будет ступенчатой

61.элементарные преобразования строк матрицы: умножение всех элементов какой либо строки отличное от нуля, прибавление к каждому элементу какой либо строки соответствующих элементов другой строки умноженных на некоторое число, перестановка строк, вычеркивание нулевой строки, транспонирование матрицы

62. алгоритм приведения матрицы к ступенчатому виду: найти первый из столбцов содержащий не нулевые элементы, выбрать строку, содержащую один из этих не нулевых элементов, выбранную строку (если она не первая) поменять местами с первой строкой; сделать нулевыми все элементы матриц под крайним элементом первой строки, в первом не нулевом столбце останется только один верхний не нулевой элемент, так будет получена первая ступень; сохраняя не изменой первую строку полученной матрицы рассмотреть матрицу из остальных строк и применить к ней предыдущие шаги описанного алгоритма

63. минором порядка К матрицы А называется определитель квадратной матрицы порядка К, полученный из матрицы А вычеркиванием каких либо строк и столбцов

64.ранг матрицы- наивысший порядок отличных от нуля миноров этой матрицы

65.минор порядка 9 некоторой матрицы отличный от нуля – ранг этой матрицы 9 или больше

66.размер матрицы А 5*7 – наибольшее значение ранга 5

67.ранг нулевой матрицы равен нулю

68. ранг =0,когда матрица нулевая

69.ранг квадратной невырожденной матрицы 5 порядка равен 5!

70.при элементарных преобразованиях строк или столбцов матриц ее ранг не изменится

71.ранг ступенчатой матрицы=кол=ву ее ненулевых строк

72.алгоритм нахождения ранга матрицы: привести данную матрицу к ступенчатому виду, вычислить ранг полученной ступенчатой матрицы, сосчитав количество ее строк ( ступенек), Ранг исходной матрицы равен рангу полученной ступенчатой матрицы

73. базисный минор матрицы – любой ненулевой минор матрицы порядок которого совпадает с рангом данной матрицы

74. столбцы матрицы е₁ , е₂ , … , е_s называются линейно зависимыми если существуют такие числа к₁ , к₂ , … , к_s не равные нулю одновременно, что линейная комбинация этих столбцов с данными коэффициентами равна нулевому столбцу

75. столбцы матрицы е₁ , е₂ , … , е_s называются линейно не зависимыми если линейная комбинация этих столбцов равна нулю только при нулевом наборе коэффициентов

76. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).

77. Строки (столбцы) матрицы называются линейно независимыми, если существует их линейная комбинация, и все коэффициенты в которой равны 0.

78.столбцы и строки матрицы элементы которых входят в базисный минор – линейно не зависимы любой столбец (строка) матрицы является линейной комбинацией этих столбцов(строк)

79. Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы.

80. вид СЛАУ: система m линейных уравнений с n неизвестными х₁,х₂,…,х_n называется система вида а₁₁х₁+а₁₂х₂+…+а_1nе_n=b₁

a₂₁х₁+а₂₂х₂+…+а_2nе_n=b_{2 ……}

а_m1х₁+а_m2х₂+…+а_mnе_n=b_m

81. коэффициенты при неизвестных образуют прямоугольную таблицу – матрицу системы а₁₁ а₁₂ … а_1n

а₂₁ а₂₂ … а_2n

a_m1 a_m2 … a_mn

82.расширенная матрица получается приписыванием к матрице системы справа столбца свободных членов (b₁ b₂ … b_m)

83. решением СЛАУ является упорядоченный набор(к₁,к₂,…,к_n) из n чисел при подстановке которых вместо соответствующих неизвестных каждое уравнение системы превращается в верное равенство.

84. совместная матрица – имеющая хотя бы одно решение

85. несовместная матрица – не имеющая ни одного решения

86. определённая матрица – совместная система имеющая одно решение

87. неопределённая матрица - совместная система имеющая более одного решения

88. однородная матрица – все свободные члены =0

89. неоднородная матрица – не все свободные члены =0

90. общее решение СЛАУ – выражение для неизвестных х₁,х₂,…,х_n, из которого может быть получено любое конкретное решение системы

91. частное решение СЛАУ - любое конкретное решение системы

92. равносильные или эквивалентные – системы уравнений имеющие одно и то же множество решений

93.СЛАУ имеет единственное решение если 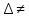0, последняя ступенька имеет 2 шага в ширину

94. метод обратной матрицы применяется к СЛАУ если в системе число уравнений совпадает с числом неизвестных и матрица А является невырожденной.

95. Метод Гаусса с помощью элементарных преобразований строк расширенная матрица Ặ приводится к ступенчатому виду.

96. теорема Крамера пусть матрицы А системы, а _J полученный из матрицы А заменой J-того столбца столбцом свободных членов. тогда если 0 то система имеет единственное решение определяемое по формулам Крамера: х_J=J/ для любого j=1,n

97. 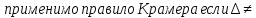0

98. система несовместна, если ранг основной и расширенной матриц системы не равны r(A)≠r(A).

99. СЛАУ совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

100. СЛАУ имеет единственное решение, если матрица А является невырожденной, т. е. ее определитель не равен нулю

101.СЛАУ имеет бесконечно много решений если

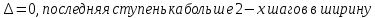
102.количество базисных неизвестных для СЛАУ, ступенчатой матрицы, равно количеству первых ненулевых элементов строк(сткпенек)

103.свободными неизвестными для СЛАУ, ступенчатой матрицы, являются остальные неизвестные(т.е. все неизвестные кроме базисных)

104.СЛАУ у которой все свободные неизвестные =0, не будет иметь нулевое решение

105.частный способ решения матричных уравнений: если А-квадр.и невырожд. матрица, то Х=А^-1В

106.общий способ решения матричных уравнений: матрицу Х выписываем подробно с неизвестными элементами, производим умножение матриц А и Х и сравниваем элементы матриц обеих частей уравнения, в результате получится СЛАУ относительно неизвестных элементов матрицы Х,эта система распадается на подсистемы вида АХ_J=B_J, решая эти системы найдём все элементы неизвестной матрицы Х, если хотя бы 1 из этих подсистем является несовместной, то данное матричное уравнение не имеет решения

107.теорема Кронекера - Капелли: СЛАУ совместна, тогда и только тогда, когда ранг расширенной матрицы Ặ системы равен рангу матрицы системы А

108. чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы. 

109.связь количества решений с рангом: если ранг матрицы совместной системы равен числу её переменных, т.е. r =n, то система имеет единственное решение а если ранг меньше числа её переменных, т.е. r <n то система неопределённая и имеет бесконечное множество решений

110.базисной подсистемой для данной системы, называется подсистема, составленная из уравнения системы на строках, их коэффициентов которых, располагается базисный минор

111.базисными неизвестными СЛАУ являются неизвестные х₁,х₂,…,х_n,, коэффициенты при которых входят в базисный минор матрицы системы, а остальные х_R+1,…,x_n – свободные неизвестные

112.фундаментальная система решений(фср) – любые n-r линейно независимых решений однородной СЛАУ

113. нормальной ФСР называется ФСР однородной СЛАУ в которой свободные неизвестные задают по формулам

114. свойства решений однородной СЛАУ: любое решение однородной СЛАУ умноженное на любое число также является решением этой системы, сумма решений однородной СЛАУ так же является её решением(из этих свойств следует что любая линейная комбинация решений однородной СЛАУ также является решением этой системы)

115. структура общего решения однородной СЛАУ: запишем расширенную матрицу и приведём её к ступенчатому виду, запишем систему определяемую полученной ступенчатой матрицей, определим базисные и свободные неизвестные, найдем их значения и запишем общее решение

116.свойства решений неоднородной СЛАУ: сумма любого решения неоднородной СЛАУ и любого решения её приведённой однородной системы является решением данной неоднородной системы, разность любых двух решений неоднородной СЛАУ является решение ее приведенной однородной системы

117.структура общего решения неоднородной СЛАУ представляет собой сумму общего решения её приведённой однородной системы и частного решения данной неоднородной системы

118. вектор - это направленный отрезок, который имеет начало и конец

119. коллинеарные векторы – лежат на одной прямой или на параллельных прямых

120. равные векторы - 2 вектора коллинеарные, имеют одинаковую длину и одинаковое направление

121. суммой a+b векторов называется вектор идущий из начала вектора а в конец вектора b если начало вектора b совпадает с концом вектора а

122. свойства сложения: a+b=b+a , (a+b)+c=a+(b+c) , для любого вектора а существует нулевой вектор 0 такой что а+0=а , для каждого вектора а существует противоположный ему вектор а’ такой что а+а’=0

123. разность а-b векторов называется вектор с который в сумме с вектором b дает вектор а

124. произведением ka вектора на число называется вектор b коллинеарный вектора а имеющий длину равную и направление совпадающее с направлением а при k>0 и противоположное а при k<0

125. свойства умножения вектора на число: k(a+b)=ka+kb , (k+m)a=ka+ma , k(ma)=(km)a

126. линейной комбинацией векторов а₁,а₂,…,а_n называется выражение вида k₁a₁+k₂a₂+…+k_na_n где k числа

127.векторы а₁,а₂,…,а_n линейно зависимы если найдутся такие числа k₁,k₂,…,k_n не все равные нулю что соответствующая линейная комбинация векторов =0, т.е. k₁a₁+k₂a₂+…+k_na_n=0

128. линейно не зависимые векторы если равенство k₁a₁+k₂a₂+…+k_na_n=0 возможно только при всех k_i=0

129. свойства линейно зависимых систем векторов: если система векторов содержит нулевой вектор то она линейно зависима, если среди n векторов какие либо (n-1) линейно зависимы то и все n векторов линейно зависимы, необходимым и достаточным условием линейной зависимости двух и трёх векторов является их компланарность, любые четыре вектора в трехмерном пространстве линейно зависимы

130. компланарные векторы – лежат либо в одной плоскости либо в параллельных плоскостях

131. базис образуют два линейно независимых вектора на плоскости (или 3 линейно независимых вектора в пространстве), если любой вектор плоскости (пространства) может быть представлен в виде их линейной комбинации

132. координаты одного вектора – числовые коэффициенты линейной комбинации в рассматриваемом базисе, если a,b,c – базис и d = ka+mb+pc то числа k, m , p координаты вектора d в базисе a,b,c

133. свойства базиса: любые два неколлинеарных вектора образуют базис на плоскости а любые три некомпланарных вектора – базис в пространстве, расположение данного вектора по данному базису единственно то есть координаты вектора в данном базисе определяются единственным образом, при сложение двух векторов их одноименные координаты складываются, при умножении вектора на число все его координаты умножаются на это число

134. проекция вектора АВ на ось U – длинна направленного отрезка A’B’ оси U где A’B’ – основание перпендикуляров опущенных из точек А и В на ось U (пр_uа )

135. свойства проекции: пр_uа = 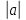cos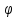 где фи угол между а и осью U; при сложении двух векторов их проекции на любую ось складываются; при умножении вектора на число его проекция на любую ось умножается на это число

136. декартовые координаты вектора d – числа х у z

137. направляющие косинусы – косинусы углов образованных векторами с осями декартовой системы координат

138. свойства направляющих косинусов: х=|d|cosα, y=|d|cosβ. z=|d|cosγ α,β,γ – углы которые данный вектор α образует с осями координат

сosα = 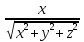, аналогично; cos²α+cos²β+cos²γ=1

139. скалярное произведение двух векторов – произведение их длин на косинус угла между ними ab=|a||b|cos

140. свойство скалярного произведения: ab=|a|пр_ab; ab=0 ab; ab=ba; (ka)b=k(ab); (a+b)c=ac+bc; a²=aa=|a|²; если векторы a и b определены своими декартовыми координатами то ab=x₁x₂ + y₁y₂ + z₁z₂; cos=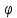

141. тройка некомпланарных векторов abc называется правой(левой) если после приведения к общему началу вектор с располагается по ту сторону от плоскости определяемой векторами а и b откуда кротчайший поворот от а и b кажется совершающимся против часовой стрелки (по часовой)

142. векторное произведение векторов - |c|=|a||b|sin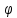; ca, c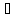b ; тройка векторов abc является правой

143. сво1ства векторного произведения: [ba]=-[ab]; [ab]=0  a||b; длинна векторного произведения равняется площади параллелограмма построенного на приведенных к общему началу векторов а и b

144. орта (орт е_а ) произвольного вектора а – вектор единичной длинны, коллиниарный а и одинакового с ним направленный

145.векторное произведение:с=, c=a*b

146.с мешанное произведение векторов a,b и с называется результат скалярного умножения векторного произведения [ab]c

147. свойства смешенного произведения: скалярное произведение [ab]c равно объему параллелепипеда построенного на приведенных к общему началу векторов a b с если они образуют правую тройку или числу противоположному этому объему, если a b с – левая тройка; если а b с компланарны то [ab]c=0

148.abc=

149. уравнение прямой проходящей через данную точку перпендикулярно данному вектору: A(x-x­­₀) + B(y-y₀)=0

150. перпендикуляр проведенный из начала координат к прямой называется нормалью прямой

151. общее уравнение прямой Ax+By+C=0

152. каноническое уравнение прямой

153. направляющий вектор прямой – вектор q

154.уравнение прямой проходящей через две заданные точки

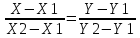
155. параметрическое уравнение прямой х=x₀+lt, y=y₀+mt

156. угловой коэффициент прямой ?

157. уравнение прямой с угловым коэффициентом y=kx+b

158. неполное уравнение прямой: с=0 – прямая Ах+Ву=0 проходит через начало координат; b=0 – прямая Ах+С=0 параллельна оси Оу; А=0 – прямая Ву+С=0 параллельна оси Ох ; В=С=0 – уравнение Ах=0 определяет ось Оу ; А=С=0 – уравнение Ву=0 определяет ось Ох

159. уравнение прямой в отрезках х/а+у/b=1

160.угол между прямыми – cos= 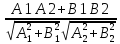A=l, B=m

161. условия параллельности прямых А₁/А₂=В₁/В₂; к₁=к₂; l₁/l₂=m₁/m₂

162. условия перпендикулярности двух прямых А₁А₂+В₁В₂=0; -к₂=-1/к₁;

163. расстояние от точки до прямой ?

164. нормальное уравнение прямой хcosα+ysinα=p

165. отклонение прямой - если d – расстояние от точки А до прямой L то отклонение δ точки А от прямой L есть число +d если точка А и начало координат лежат по разные стороны от прямой L и число –d если они лежат по одну сторону

166. теорема отклонения прямой: отклонение точки А от прямой L, заданной нормальным уравнением определяется: δ=х₁cosα+y₁sinα-p

167. уравнение плоскости проходящей через данную точку перпендикулярно данному вектору: A(x-x₀)+B(y-y₀)+C(z-z₀)=0

168. общее уравнение плоскости: Ax+By+Cz+D=0

169. неполное уравнение плоскости: D=0 – плоскость Ax+By+Cz=0 проходит через начало координат, А=0, В=0 – плоскость Ax+By+Cz=0 параллельна оси Оу, С=0 - плоскость Ax+By+Cz=0 параллельна оси Оz, А=В=0 – плоскость Сz+D=0 параллельно координатной плоскости Оху , А=С=0 – плоскость Ву+D=0 параллельно координатным плоскости Оуz, А=D=0 – плоскость Ву+Сz=0 проходит через ось Ох, В=D=0 – плоскость Ах+Сz=0 проходит через ось Оу, С=D=0 – плоскость Ах+Ву=0 проходит через ось Оz, А=В=D=0 – уравнение Cz=0 задает координатную плоскость Оху, А=С=D=0 получаем Ву=0 уравнение координатной плоскости Охz, B=C=D=0 плоскость Ах=0 является координатной плоскостью Оуz

170. уравнение плоскости в отрезках : х/а + у/b + z/c = 1

171. угол между плоскостями cos=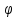

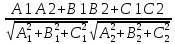
172. условие параллельности плоскостей: А₁/А₂=В₁/В₂=С₁/С₂

173. условие перпендикулярности плоскостей А₁А₂+В₁В₂ +С₁С₂=0

174. уравнения плоскости проходящей через три данные точки 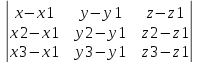= 0

175. нормальное уравнение плоскости : хcosα+ycosβ+zcosγ-p=0

176. расстояние от точки до плоскости d=|хcosα+ycosβ+zcosγ-p|

177. направляющий вектор прямой – любой не нулевой вектор параллельный данной прямой

178. каноническое уравнение прямой

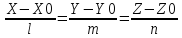
179. уравнение прямой проходящей через две данные точи (Х-Х1)/(Х2-Х1)=(У-У1)/(У2-У1)=(Z-Z1)/(Z2-Z1)

180.параметрическое уравнение прямой

181.угол между прямыми в пространстве равен углу между их направляющими векторами

182. условие параллельности прямых l₁/l₂=m₁/m₂=n₁/n₂

183. условие перпендикулярности прямых l₁l₂+m₁m₂+n₁n₂=0

184. угол между прямой и плоскостью 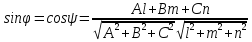185. Условие параллельности прямой и плоскости Аl+Bm+Cn=0

186. условие перпендикулярности прямой и плоскости А/l=B/m=C/n

187.

188. базисом в линейном пространстве называется набор линейно независимых векторов е₁,е₂,…,e_n, такой, что любой вектор Х этого пространства

можно представить в виде: Х=х₁е₁+х₂е₂+…+х_ne_n =( е₁,е₂,…,e_n)*(х₁)

(х₂)= e(x)_e

(х_n)

189. размерность-кол-во векторов в любом базисе линейного пространства.

190. Числа х₁,х₂,…,х_n – координаты вектора Х в базисе Е.

191. если размерность пространства n, то его называют n-мерным.

192. матрицей перехода от базиса е к базису е’ называется матрица Т, столбцами которой , являются координатные столбцы векторов нового базиса е’ в старом базисе е.

194. линейным оператором(лин. преобразованием) в линейном пространстве называется отображение Ặ пространства на себя, при котором для любых векторов х, у этого пространства и для любого вещественного числа α выполняется: Ặ(х+у)= Ặх+ Ặу, Ặ(αх)=α(Ặх).

195. матрица линейного оператора – матрица А столбцами которой являются координатные столбцы образов Ặ_еi векторов базиса е в базисе е’:

Ặ_еi=а_1ie₁+ а_2ie₂+…+ а_nie_n , A=(a_ij)

196.A- матрица линейного оператора в базисе е, а А’- в новом базисе е’, Т- матрица перехода от базиса е к е’ : А’=Т^-1АТ

198.собственный вектор матрицы А и оператора Ặ– ненулевой вектор х, если выполняется одно из равенств: Ặх=λх, Ах=λх, где λ действительное число(собственное число матрицы оператора)

199. собственные числа, это те числа, которые получаются в решении, когда определитель матрицы =0

200. характеристическое уравнение – это уравнение вида 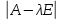=0

201.характеристический многочлен – это многочлен определяющий ее собственные значения

202. 1) A-𝝀E 2) 3) =0 находим 𝝀(собственные числа)

203.квадратичной формой действительных переменных х₁,х₂,…,х_n,, называется многочлен второй степени относительно этих переменных не содержащий свободного члена и членов первой степени