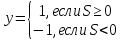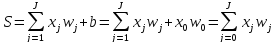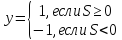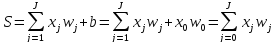- •Основные методы представления знаний в экспертных системах. Этапы (прототипы) разработки экспертной системы. Коллектив разработчиков экспертной системы.
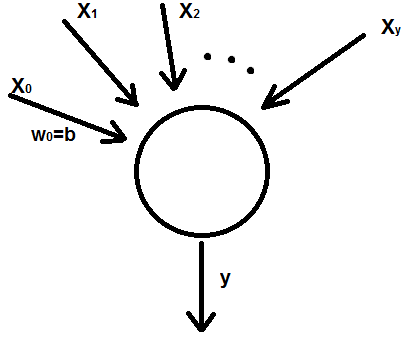
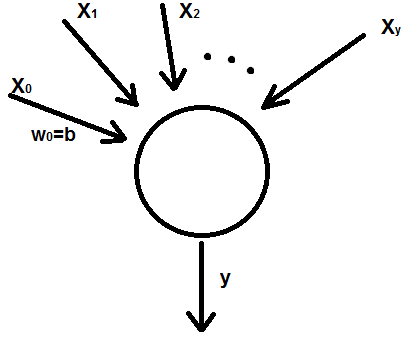
- •Математический нейрон. Его графическое изображение, формулы по которым он работает, виды активационных функций. Моделирование основных логических функций с помощью математического нейрона
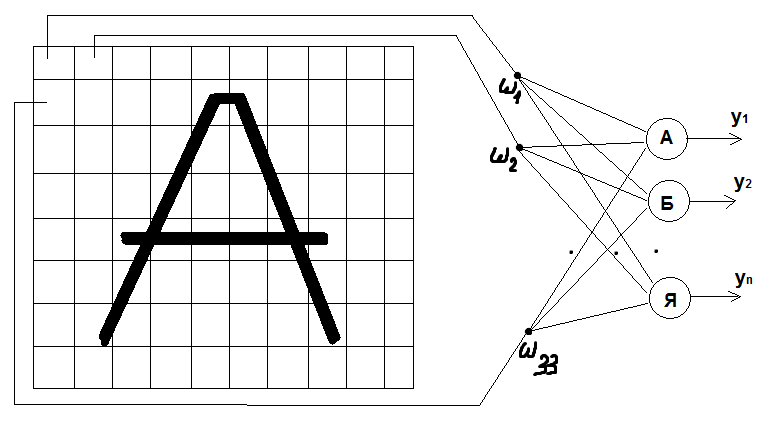
- •Персептрон Розенблатта, его принцип действия на примере распознавания букв.
- •Сравнительный анализ процедурной, функциональной, объектно-ориентированной и логической парадигм программирования.
- •Этапы и методологии проектирования баз данных.
- •Программное обеспечение для проектирования, реализации проектов информационных систем. (case-технологии, субд и пр.)
- •Представление числовых величин в эвм: позиционные системы счисления; форматы чисел с фиксированной и плавающей точкой; представление в прямом, обратном и дополнительном кодах.
- •Принципы организации машины фон Неймана.
- •6) Представительский уровень
- •7) Прикладной уровень
- •Основы теории моделирования информационных систем и протекающих в них процессов.
- •Аналитические методы моделирования (ам)
- •Имитационные методы моделирования (им)
- •Функциональные методы моделирования (фм)
- •Статическое моделирование (см)
- •Криптография как наука. Основные понятия и определения
- •Электронная цифровая подпись. Гост р 34.10-2001
- •Управление оперативной памятью в современных операционных системах: управление физической и виртуальной памятью, способы организация виртуальной памяти, организация подкачки.
- •Управление хранением данных: система накопителей информации, система драйверов накопителей информации, современные файловые системы.
- •Обходы графов, эйлеровы и гамильтоновы графы, алгоритм Флери. Укладки графов, изоморфизм, гомеоморфизм, планарность, критерий планарности, формула Эйлера.
- •Двудольные графы, критерий двудольности, деревья, остовные деревья
- •Экстремальные задачи теории графов, «жадные» алгоритмы, алгоритм Дейкстры
- •Раскраски графов, «жадный» алгоритм. Хроматическое число, хроматический многочлен, его нахождение и свойства.
- •Элементарные булевы функции и способы их задания, существенные и фиктивные переменные. Разложение булевых функций по переменным, сднф, скнф, полиномы Жегалкина.
- •Повторные выборки, сочетания и размещения (с возвращением и без возвращения элементов). Комбинаторные принципы.
- •Биномиальные и полиномиальные коэффициенты, бином Ньютона, треугольник Паскаля. Полиномиальная формула.
- •Алфавитное кодирование: необходимое и достаточные условия однозначности декодирования, теорема Маркова, алгоритм Маркова.
- •Коды с минимальной избыточностью (коды Хаффмана), метод построения. Самокорректирующиеся коды (коды Хэмминга), метод построения.
- •Недетерминированные двухполюсные источники, замкнутые множества состояний. Задача синтеза автоматов-распознавателей.
- •Эквивалентные состояния, эквивалентные автоматы, минимизация автоматов, алгоритм Мили.
- •Особенности организации операционной системы Unix. Цели создания и структура операционной системы.
- •Понятие сложности алгоритма и сложности (объема) входных данных. Основные правила вычисления сложности алгоритма (сложность линейного алгоритма, ветвления, цикла).
-
Математический нейрон. Его графическое изображение, формулы по которым он работает, виды активационных функций. Моделирование основных логических функций с помощью математического нейрона
Математический нейрон – устройство, моделирующее мозг человека.
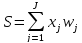 ,
,
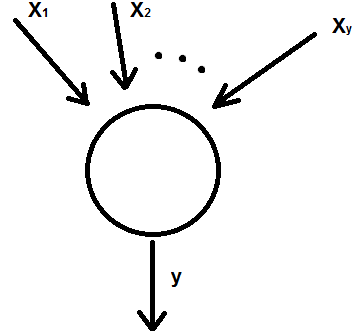
где
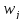 – весевой коэффициент (сила синаптических
связей)
– весевой коэффициент (сила синаптических
связей)
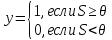 – формула
МакКалока и Питса;
– формула
МакКалока и Питса;
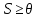 -
возбуждение нейрона.
-
возбуждение нейрона.
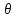 – порог
чувствительности нейрона
– порог
чувствительности нейрона
Активационная функция:
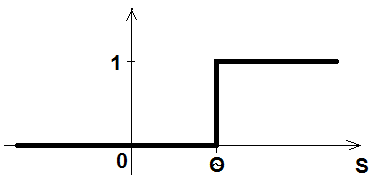
Модификации формулы:
-
Пусть
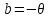 :
:
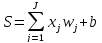 ;
;
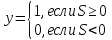 Активационная
функция:
Активационная
функция:
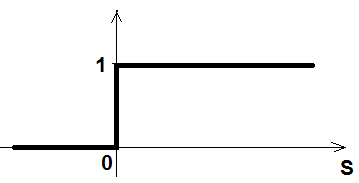
В нейронных сетях значения хранятся в виде сил синоптических связей.
Синапс – измеряют величину обратного сопротивления (электропроводность или сила синоптических связей).
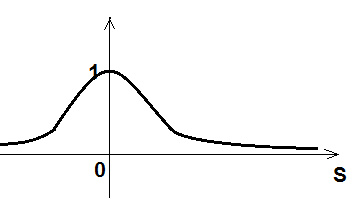
Виды активационных функций:
-
Ступенька (пороговые):
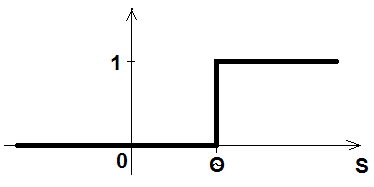
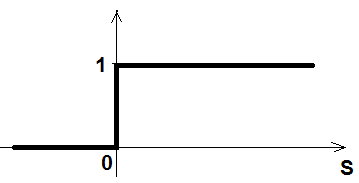
-
Линейные:
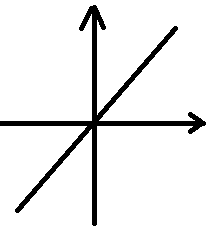
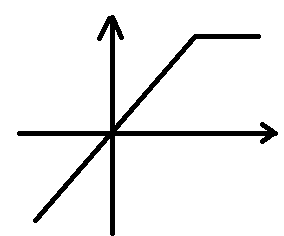
-
Сигомоидные (возникает паралич сети)
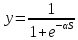
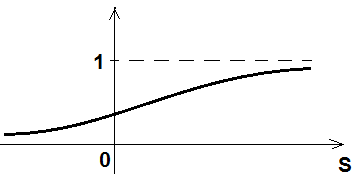
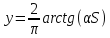
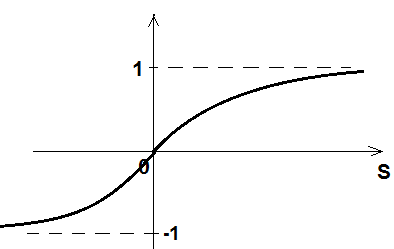
-
Логарифм (не имеет асимптот)
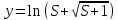

-
Радиально-базисная
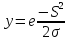
Моделирование основных логических функций с помощью математического нейрона:
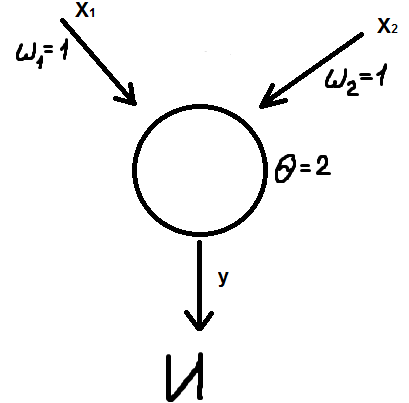
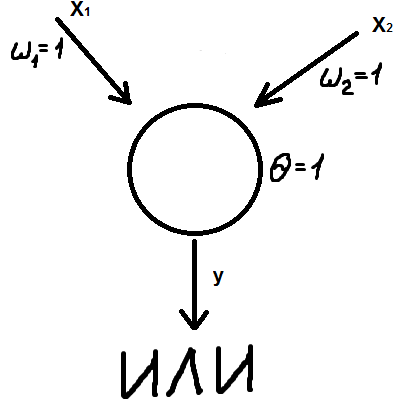

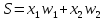
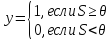
(Проверить для X1 и X2)
-
Персептрон Розенблатта, его принцип действия на примере распознавания букв.
Розенблатт построил первый нейрокомпьютер.
Модификации формулы:
-
Пусть
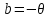 :
:
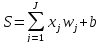 ;
;
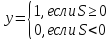 Активационная
функция:
Активационная
функция:
Распознование букв:
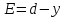 ,
где
,
где
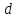 – желаемый
выход
– желаемый
выход
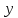 – действительный
выход
– действительный
выход
Для «А» D=(1,0,0…,0); «Б» D=(0,1,0,…,0)
т.е. для «А» y1=1; y2…y33=0
для «Б» y1=0; y2=1; y3…y33=0
-
Датчики случайных чисел всем синаптическим весам и порогу чувствительности присвоить какие-то случайные значения.
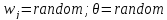
-
Предъявить персептрону какую-либо букву
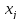 ,
получить вектор;
x0=1;
,
получить вектор;
x0=1; -
Нейрон выполняет взвешанное суммирование сигнала. y-?
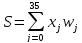 ;
;
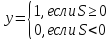
-
Вычисление погрешности
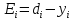
-
Корректировка весовых коэффициентов
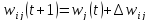 ;
;
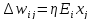
-
Повторение шагов 2-5.
Теорема Розенблата:
Если существует множество значений синаптических весов, которые обеспечивают требуемое распознование образов, то в конечном итоге алгоритм обучения персептрона приведет либо к этому множеству, либо к другому множеству, такому что требуемое распознование образа будет достигнуто при условии, что это множество существует.
-
Алгоритм проектирования нейронной сети слоистой структуры (персептрона). Привести пример проектирования персептрона в одной из областей: промышленность, экономика, социология, политология, медицина, криминалистика, спорт и др.
Алгоритм нейросетевого математического моделирования:
-
Постановка задачи Определяются цели задачи; входные и выходные – структура X, D (компоненты векторов D, X числовые, иначе кодирование в цифры). В результате получаем структуру X, D
-
Формирование примеров Формируется содержимое векторов D,X; X1-D1, X2-D2 … XqDq – множество примеров предметной области (способы формирования: анкетирование, интернет); Множество примеров Q разбивается на 3 множества: L (обучающее), T (тестирующее), Р (проверяющее). Q=7Nx+15, где Nx – число входных параметров. Для T и Р берется по 10-15% примеров от количества примеров множества L.
-
Проектирование сети определяется число Nx, Ny, N, Nw, Q, активационная функция Nx – число входных параметров. Ny – количество выходных параметров N – число нейронных сетей скрытого слоя Nw – необходимое количество сил синаптических связей Q – количество примеров
-
Обучение Корректировка весов (подбор таких синаптических весов, чтоб на каждый входной сигнал выдавал y=d) Причины необучения: - мало нейронов на скрытом слое; - наличие на обучающем множестве противоречащих друг другу примеров; - наличие посторонних выбросов
-
Проверка и оптимизация сети Проверка на тестирующем множестве, вычисление погрешности (постройка гистрограмм). Тестирование на подтверждающем множестве (тестирование на нем только один раз) Если погрешность слишком большая, то необходимо внести корректировки последовательно в 4, 3, 2, 1 пунктах.
-
Исследование моделей, прогнозирование Адекватна ли модель предметной области. Проводить эксперементы с математической моделью (выдавать рекомендации).
Пример: Проектирование персептрона в медецине.
-
Определяем какие вопросы будет система задавать пациенту (кашель, насморк и прочее); определяем какие болезни возможны при таких симптомах
-
Формируются примеры на основе больничных карт и прочее
-
Определяем Nx, Ny, N, Nw, Q. Nx, Ny - известно Q=7Nx+15
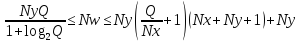
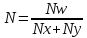 Разбиваем
Q
на три множества (L,
T,
P)
Разбиваем
Q
на три множества (L,
T,
P) -
Обучение
-
Проверка и оптимизация сети
-
Исследование