
- •Основные методы представления знаний в экспертных системах. Этапы (прототипы) разработки экспертной системы. Коллектив разработчиков экспертной системы.
- •Математический нейрон. Его графическое изображение, формулы по которым он работает, виды активационных функций. Моделирование основных логических функций с помощью математического нейрона
- •Персептрон Розенблатта, его принцип действия на примере распознавания букв.
- •Сравнительный анализ процедурной, функциональной, объектно-ориентированной и логической парадигм программирования.
- •Этапы и методологии проектирования баз данных.
- •Программное обеспечение для проектирования, реализации проектов информационных систем. (case-технологии, субд и пр.)
- •Представление числовых величин в эвм: позиционные системы счисления; форматы чисел с фиксированной и плавающей точкой; представление в прямом, обратном и дополнительном кодах.
- •Принципы организации машины фон Неймана.
- •6) Представительский уровень
- •7) Прикладной уровень
- •Основы теории моделирования информационных систем и протекающих в них процессов.
- •Аналитические методы моделирования (ам)
- •Имитационные методы моделирования (им)
- •Функциональные методы моделирования (фм)
- •Статическое моделирование (см)
- •Криптография как наука. Основные понятия и определения
- •Электронная цифровая подпись. Гост р 34.10-2001
- •Управление оперативной памятью в современных операционных системах: управление физической и виртуальной памятью, способы организация виртуальной памяти, организация подкачки.
- •Управление хранением данных: система накопителей информации, система драйверов накопителей информации, современные файловые системы.
- •Обходы графов, эйлеровы и гамильтоновы графы, алгоритм Флери. Укладки графов, изоморфизм, гомеоморфизм, планарность, критерий планарности, формула Эйлера.
- •Двудольные графы, критерий двудольности, деревья, остовные деревья
- •Экстремальные задачи теории графов, «жадные» алгоритмы, алгоритм Дейкстры
- •Раскраски графов, «жадный» алгоритм. Хроматическое число, хроматический многочлен, его нахождение и свойства.
- •Элементарные булевы функции и способы их задания, существенные и фиктивные переменные. Разложение булевых функций по переменным, сднф, скнф, полиномы Жегалкина.
- •Повторные выборки, сочетания и размещения (с возвращением и без возвращения элементов). Комбинаторные принципы.
- •Биномиальные и полиномиальные коэффициенты, бином Ньютона, треугольник Паскаля. Полиномиальная формула.
- •Алфавитное кодирование: необходимое и достаточные условия однозначности декодирования, теорема Маркова, алгоритм Маркова.
- •Коды с минимальной избыточностью (коды Хаффмана), метод построения. Самокорректирующиеся коды (коды Хэмминга), метод построения.
- •Недетерминированные двухполюсные источники, замкнутые множества состояний. Задача синтеза автоматов-распознавателей.
- •Эквивалентные состояния, эквивалентные автоматы, минимизация автоматов, алгоритм Мили.
- •Особенности организации операционной системы Unix. Цели создания и структура операционной системы.
- •Понятие сложности алгоритма и сложности (объема) входных данных. Основные правила вычисления сложности алгоритма (сложность линейного алгоритма, ветвления, цикла).
-
Двудольные графы, критерий двудольности, деревья, остовные деревья
Двудольный граф – граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.
Критерий двудольности.
Теорема 1. Граф является двудольным тогда и только тогда, когда для его правильной вершинной раскраски достаточно двух цветов.
Теорема 2. Граф двудольный тогда и только тогда, когда в нем все циклы имеют четную длину.
Деревья.
Дерево – связный граф без циклов.
Свойства:
-
Любое ребро является мостом.
-
Из любой вершины в любую другую существует только один простой путь
-
Добавление ребра всегда приводит к образованию цикла
-
Если в дереве n>=2, то обязательно существует не менее двух концевых вершин и не менее одного концевого ребра.
-
Если в дереве n>=3, то в дереве есть хотя бы одна внутренняя вершина (не концевая).
-
Если в дереве n вершин, то в нем n-1 ребер.
Остовное дерево – это дерево, которое получается из исходного графа удалением некоторых его ребер (вершины графа удалять нельзя!).
Алгоритмы построения минимального остовного дерева:
Алгоритм Прима.Построение начинается с дерева, включающего в себя одну (произвольную) вершину. В течение работы алгоритма дерево разрастается, пока не охватит все вершины исходного графа. На каждом шаге алгоритма к текущему дереву присоединяется самое лёгкое из рёбер, соединяющих вершину из построенного дерева, и вершину не из дерева.
Алгоритм Краскала.Вначале текущее множество рёбер устанавливается пустым. Затем, пока это возможно, проводится следующая операция: из всех рёбер, добавление которых к уже имеющемуся множеству не вызовет появление в нём цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких рёбер больше нет, алгоритм завершён. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным деревом минимального веса.
-
Экстремальные задачи теории графов, «жадные» алгоритмы, алгоритм Дейкстры
-
Задача коммивояжера. NP-полная задача
Дан полный граф (любые 2 вершины соединены ребром). Найти гамильтонов цикл min длины.
«Жадный» (приближенный) алгоритм – все время идти по короткой дороге.
ПРИМЕР:
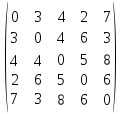 матрица
расстояний графа К5
матрица
расстояний графа К5
A ->B ->E ->C ->D ->A
3 3 8 5 2 = 21
-
Задача нахождения минимального остовного дерева.
Алгоритм Прима.Построение начинается с дерева, включающего в себя одну (произвольную) вершину. В течение работы алгоритма дерево разрастается, пока не охватит все вершины исходного графа. На каждом шаге алгоритма к текущему дереву присоединяется самое лёгкое из рёбер, соединяющих вершину из построенного дерева, и вершину не из дерева.
Алгоритм Краскала.Вначале текущее множество рёбер устанавливается пустым. Затем, пока это возможно, проводится следующая операция: из всех рёбер, добавление которых к уже имеющемуся множеству не вызовет появление в нём цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких рёбер больше нет, алгоритм завершён. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным деревом минимального веса.
-
Нахождение кратчайшего пути в графе. Алгоритм Дейкстры.
Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до некоторой вершины a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.
ПРИМЕР:
Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.

Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.
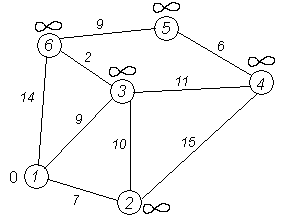
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
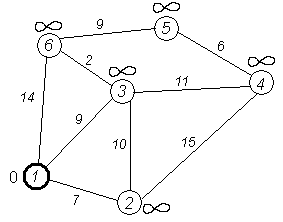
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значению её метки, и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.
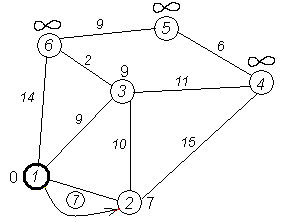
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.

Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
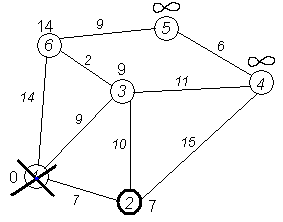
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.
Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
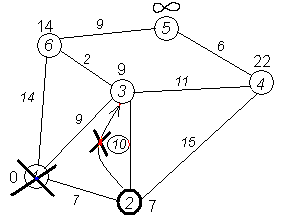
Ещё
один сосед вершины 2 — вершина 4. Если
идти в неё через 2-ю, то длина такого пути
будет равна сумме кратчайшего расстояния
до 2-й вершины и расстояния между вершинами
2 и 4, то есть 22 (7 + 15 = 22). Поскольку 22<![]() ,
устанавливаем метку вершины 4 равной
22.
,
устанавливаем метку вершины 4 равной
22.

Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.

Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
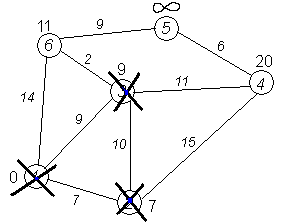
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.
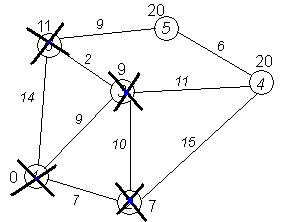
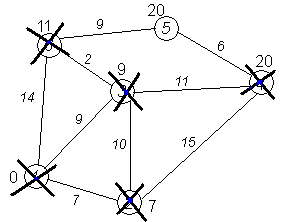
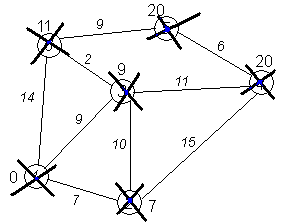
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда нельзя больше обработать ни одной вершины. В данном примере все вершины зачеркнуты, однако ошибочно полагать, что так будет в любом примере - некоторые вершины могут остаться незачеркнутыми, если до них нельзя добраться. Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
