Лекция 15
15. Расчет допусков на отклонение формы, поворота, расстояние поверхностей детали и методы их оценки
15.1. Расчет допусков на отклонение формы, поворота и расстояние поверхностей детали
Для того, чтобы нагляднее представить различие в методиках расчета допусков на отклонение формы, поворота и расстояние поверхностей идеальных и реальных деталей, рассмотрим пример. Предположим, необходимо при изготовлении СЕ, состоящих из трех деталей (рис.15.1), ограниченных плоскими поверхностями и имеющими одинаковые номинальные размеры, обеспечить расстояние L между точкой В и поверхностью А.
а)
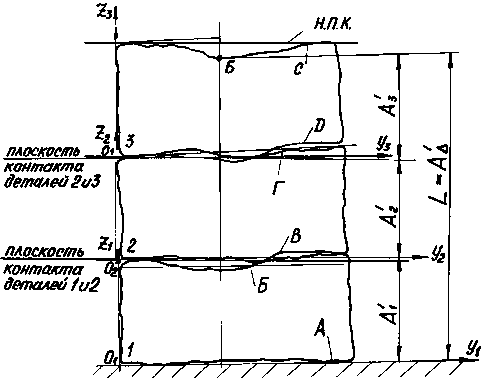
б)
Рис.15.1. Модель сборочной единицы с идеальными поверхностями (а) и с реальными поверхностями (б) детали
В том случае, когда
СЕ собрано из деталей с идеальными
поверхностями (рис.15.1а) расчет допуска
выполняется следующим образом.
Поставленная задача
решается
с помощью размерной цепи
,
уравнение которой выглядит так:
.
Допустим, что служебное назначение СЕ требует обеспечения достаточно жесткого допуска:
;
.
Использование метода неполной взаимозаменяемости позволяет, при некотором риске выхода за пределы допуска значений замыкающего звена, значительно расширить допуски на составляющие звенья. При этом допуск на замыкающее звено можно определить:
,
а допуск на i-е составляющее звено составит:
,
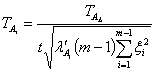Для принятых
значений
,
,
и
t=3,
,
,
m=4 допуск на составляющее звено равен:
.
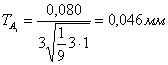Координаты середин полей составляющих звеньев также будут установлены одинаковыми
,
что в числах
составит:
.
В принятой методике
расчет допусков заканчивается расчетом
допусков только на расстояние (размер).
допуски
на форму поверхностей и их относительный
поворот считаются либо «невыходящими»
за пределы допуска на размер, либо
задаются долей допуска на размер в
зависимости от степени точности (25%,
40%, 60%).
Схема распределения допуска приведена на рис. 15.2.
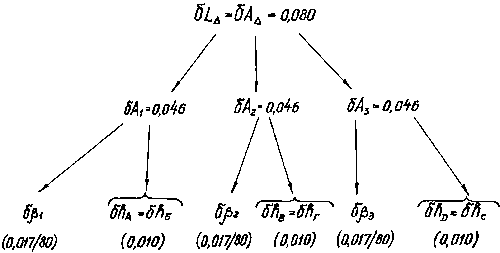
Рис.15.2. Схема распределения допуска принятым методом
В том случае, когда СЕ собрана из деталей с реальными поверхностями (рис.15.1.б) расчет допусков необходимо выполнять иначе.
Замыкающее звено
между
точкой
и
поверхностью
,
также представляет собой сумму трех
слагаемых:
.
В отличие от
размерной цепи
,
представленной на рис.15.1а, составляющими
звеньями размерной цепи
(рис.15.1
б) являются либо отрезки прямой Б-Б,
заключенные между координатными
плоскостями
,
являющимися плоскостями контакта
соответствующих деталей (
и
,
либо отрезком той же прямой, заключенной
между плоскостью контакта и нулевой
плоскостью контакта
.
Звено
при
этом представляет собой:
,
где
–
соответственно расстояние между
вспомогательной и основной базами
детали представляющее собой отрезок
оси
,
отсекаемый нулевой плоскостью контакта;
–
величина отклонения
значения
в
сечении
из-за
наличия собственного поворота поверхностей
детали;
–
величина несовпадения
нулевой плоскости контакта и плоскости
контакта:
,
.
В отличие от звеньев
и
,
звено
определяется:
,
где
–
отклонение от плоскостности поверхности
в
точке
.
После подстановки
всех значений в уравнение можно определить
:
.
Раскрыв значения слагаемых, и записав их в другой последовательности, получим:
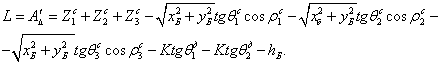
Введя обозначения:
-
; -
; -
; -
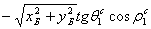
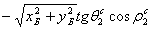
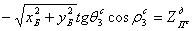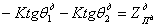получим уравнение
,
отображающее влияние на замыкающее
звено трех видов отклонений поверхностей
деталей, входящих в СЕ. Действительно,
слагаемое
учитывается
влияние отклонений собственно расстояний
между поверхностями основных и
вспомогательных баз детали;
влияние
относительного поворота поверхностей
баз и их формы;
–
отклонение формы исполнительной
поверхности.
Это уравнение
требует, чтобы допуски, ограничивающие
указанные отклонения, были подчинены
зависимости:
,
что приводит к схеме назначения допусков,
представленной на рис.15.3.
Учитывая сложность
соблюдения каждого из слагаемых
уравнения, были назначены допуски:
,030
мм;
0,044
мм;
=0,006
мм. Координаты середин полей допусков
были рассчитаны обычным методом. Их
значения равны:
=-0,066
мм;
=0;
=-0,003
мм.
Предельные значения
замыкающего звена СЕ
:
,
.
Формулы, рассмотренные выше, позволили рассчитать все показатели, приведенные в схеме (рис.15.3).
Рис.15.3 Схема распределения допусков с учетом погрешностей формы, поворотов и расстояний