1.9. Теорема Гаусса для электрического поля в диэлектриках

При поляризации диэлектрика в каждом небольшом его объеме происходит упорядочение в направлении дипольных моментов его молекул. В результате каждую область диэлектрика можно охарактеризовать некоторым суммарным дипольным моментом (равным векторной сумме дипольных моментов отдельных молекул). Для того, чтобы охарактеризовать состояние поляризации диэлектрика в каждой небольшой его области, вводят понятие вектора поляризации . Вектором поляризации называют дипольный момент единицы объема диэлектрика. В различных областях диэлектрика векторможет быть разным. 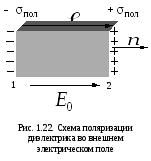Поляризация, при которой векторв каждой небольшой области диэлектрика один и тот же, называется однородной. Очевидно, что однородно поляризованным будет диэлектрик, помещенный в однородное внешнее электрическое поле.

Пусть диэлектрик помещен в однород­ное внешнее электрическое поле . Мыс­лен­но вырежем из диэлектрика прямо­уголь­ный параллелепипед, реброкоторого параллельно. Поверхностную плотность поляризационных зарядов на гранях 1 и 2 обо­значим и(рис. 1.22). Рассчи­та­ем суммарный дипольный момент парал­ле­ле­пипеда. Можно считать, что наш образец состоит из ряда диполей длинойи дипольными моментами, где–i-й поляризационный заряд на грани 2. Суммарный дипольный момент образца равен

,

где  площадь каждой из граней 1 и 2. Тогда согласно данному определению вектор поляризации:

.

Проекция вектора поляризации на направление нормали к грани 2:

. (1.22)

Уравнение (1.22) можно записать в виде: . Полный поляризационный заряд на поверхностидиэлектрика в общем случае определяется поверхностным интегралом:

.

Полученное выражение имеет общий характер. Оно будет справедливо и в случаях, когда поляризационные заряды находятся на неплоских поверхностях и поляризация неоднородна. Итак, проекция вектора поляризации на направление нормали к поверхности равна суммарному заряду, смещенному при поляризации диэлектрика вдоль нормали через единичную площадь. Выражение (1.22) показывает, что вектор поляризации измеряется в .

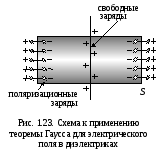
Теперь рассмотрим применение тео­ре­мы Гаусса для электрического поля в диэлектриках. Для определенности выбе­рем равномерно заряженную плоскость, находящуюся в какой-либо диэлек­три­чес­кой среде (рис. 1.23). Так же как и в при­ме­ре 1.3, в качестве произвольной поверх­но­сти выберем цилиндр длиной, ось ко­то­рого перпендикулярна плоскости, а основания равноудалены от нее. Теперь внутрь поверхностипопадут не только свободные заряды, находящиеся на плос­ко­сти, но и связанные заряды, появля­ю­щиеся вследствие поляризации ди­элек­трической среды (на рис. 1.23 показаны диполи, «разрезанные» поверхностьюна две части – отрицательные заряды этих диполей оказались внутри поверхности). Поэтому теорему Гаусса (1.18) в этом случае правильно будет записать в следующем виде:

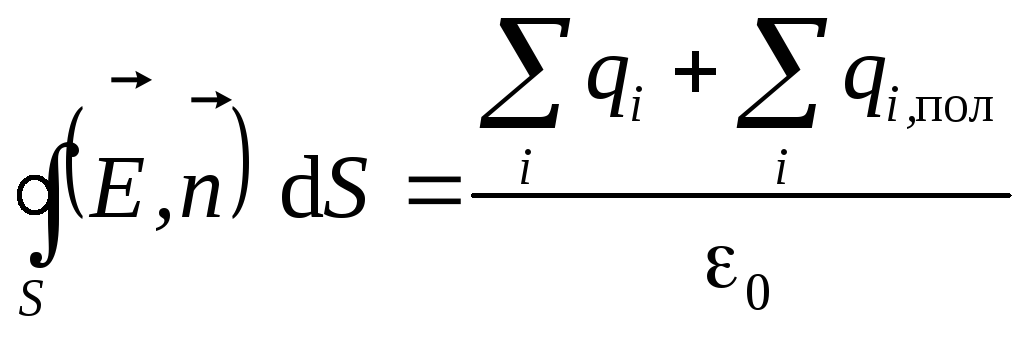, (1.23,а)

где  сумма свободных зарядов, находящихся внутри поверхности , а сумма нескомпенсированных связанных или поляризационных зарядов, находящихся внутри поверхности .

С другой стороны, из опыта известно, что электрическое поле в диэлектрике уменьшается в некоторое число раз по сравнению с полем в вакууме. Это число называется диэлектрической проницаемостью среды и обозначается . Величина  зависит только от свойств диэлектрика и не зависит от величины внешнего электрического поля. Такое уменьшение электрического поля в диэлектрике можно было бы учесть, «поправив» теорему Гаусса следующим образом:

. (1.23,б)

Выражения (1.23,а) и (1.23,б) – суть одно и тоже. На практике для определения электрического поля в диэлектрических средах, конечно, пользуются выражением (1.23,б), поскольку сумма поляризационных зарядов, попавших внутрь какой-либо поверхности в объеме диэлектрика – величина неизвестная, а величина  для каждого диэлектрика определена экспериментально.

Введем новый вектор:

, (1.24)

называемый вектором электрического смещения. Теорему Гаусса для электрического поля в диэлектриках можно записать через вектор . Простые преобразования выражения (1.23,б) дают следующий результат:

. (1.23,в)

Поскольку в правой части выражения (1.23,в) осталась только сумма свободных зарядов (сравните с формулой 1.23,а), говорят, что вектор электрического смещения характеризует электрическое поле только свободных зарядов (или определяется только свободными зарядами). При одном и том же распределении свободных зарядов этот вектор будет одним и тем же, не зависимо от среды, в которой находятся эти заряды.

Все заряженные объекты, рассматриваемые в примерах 1.3 - 1.6, можно проанализировать теперь и в диэлектрической среде. Для этого нужно использовать теорему Гаусса в виде (1.23,б) или (1.23,в). Естественно, что в полученных результатах для напряженностей и потенциалов всякий раз будет появляться величина диэлектрической проницаемости в знаменателе. Например, поле заряженной плоскости (см. пример 1.3) определяется выражением:

, (1.20,а)

а поле между двумя противоположно заряженными плоскостями (см. пример 1.4):

. (1.20,б)

Если полая равномерно заряженная сфера (или металлический шар) (см. пример 1.5) находятся в диэлектрике, то при напряженность электрического поля сферы

,

а потенциал

.

Потенциал самой сферы

.

В заключение отметим, что между тремя векторами ,исуществует связь, определяемая уравнением:

. (1.25)

Для доказательства этой связи воспользуемся картиной поляризации диэлектрика, изображенной на рис.1.23. Запишем теорему Гаусса для электрического поля в диэлектрической среде (1.23,а и 1.23,в):

, .

Из этих уравнений следует:

.

Учитывая, что поляризационные заряды, попавшие внутрь цилиндра , отрицательны

,

получим:

,

откуда и следует уравнение (1.25).

Комбинируя (1.24) и (1.25), можно получить:

или: (1.26)

Величина называется поляризуемостью диэлектрика.